Nhan H. Pham
Evaluating Robustness of Cooperative MARL: A Model-based Approach
Feb 07, 2022



Abstract:In recent years, a proliferation of methods were developed for cooperative multi-agent reinforcement learning (c-MARL). However, the robustness of c-MARL agents against adversarial attacks has been rarely explored. In this paper, we propose to evaluate the robustness of c-MARL agents via a model-based approach. Our proposed formulation can craft stronger adversarial state perturbations of c-MARL agents(s) to lower total team rewards more than existing model-free approaches. In addition, we propose the first victim-agent selection strategy which allows us to develop even stronger adversarial attack. Numerical experiments on multi-agent MuJoCo benchmarks illustrate the advantage of our approach over other baselines. The proposed model-based attack consistently outperforms other baselines in all tested environments.
Federated Learning with Randomized Douglas-Rachford Splitting Methods
Mar 05, 2021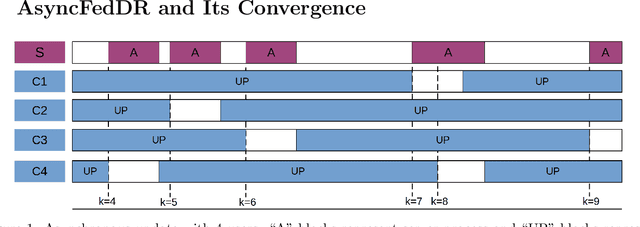
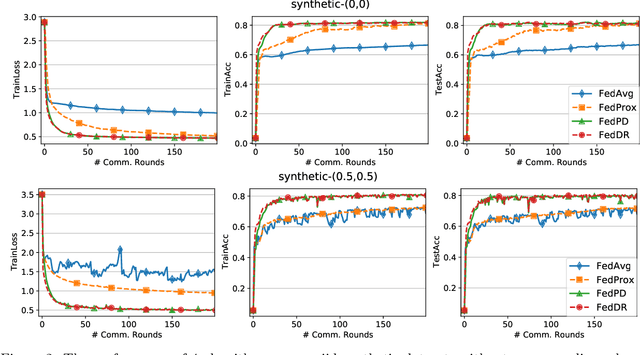
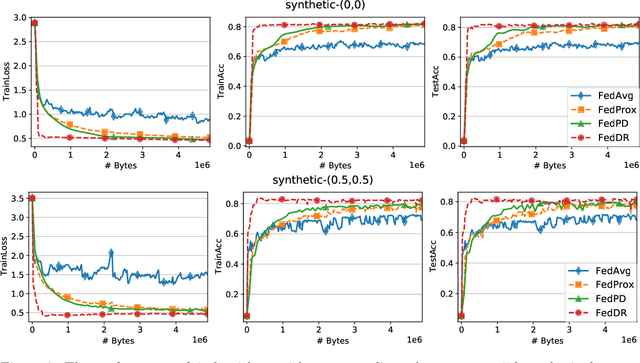
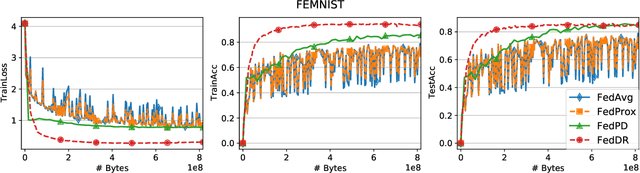
Abstract:In this paper, we develop two new algorithms, called, \textbf{FedDR} and \textbf{asyncFedDR}, for solving a fundamental nonconvex optimization problem in federated learning. Our algorithms rely on a novel combination between a nonconvex Douglas-Rachford splitting method, randomized block-coordinate strategies, and asynchronous implementation. Unlike recent methods in the literature, e.g., FedSplit and FedPD, our algorithms update only a subset of users at each communication round, and possibly in an asynchronous mode, making them more practical. These new algorithms also achieve communication efficiency and more importantly can handle statistical and system heterogeneity, which are the two main challenges in federated learning. Our convergence analysis shows that the new algorithms match the communication complexity lower bound up to a constant factor under standard assumptions. Our numerical experiments illustrate the advantages of the proposed methods compared to existing ones using both synthetic and real datasets.
Finite-Time Analysis of Stochastic Gradient Descent under Markov Randomness
Apr 01, 2020Abstract:Motivated by broad applications in reinforcement learning and machine learning, this paper considers the popular stochastic gradient descent (SGD) when the gradients of the underlying objective function are sampled from Markov processes. This Markov sampling leads to the gradient samples being biased and not independent. The existing results for the convergence of SGD under Markov randomness are often established under the assumptions on the boundedness of either the iterates or the gradient samples. Our main focus is to study the finite-time convergence of SGD for different types of objective functions, without requiring these assumptions. We show that SGD converges nearly at the same rate with Markovian gradient samples as with independent gradient samples. The only difference is a logarithmic factor that accounts for the mixing time of the Markov chain.
A Hybrid Stochastic Policy Gradient Algorithm for Reinforcement Learning
Mar 01, 2020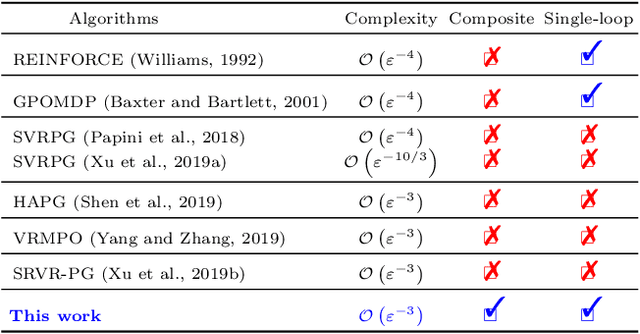
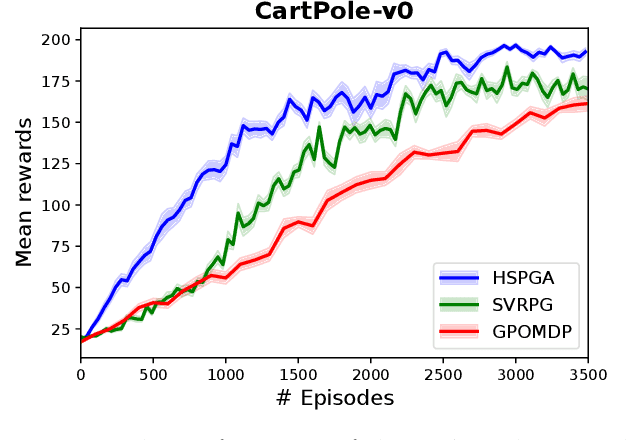
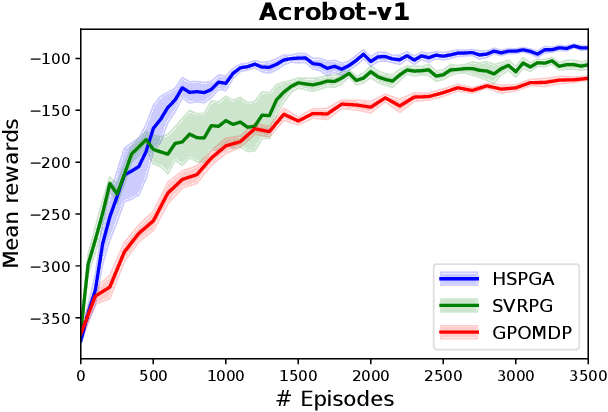
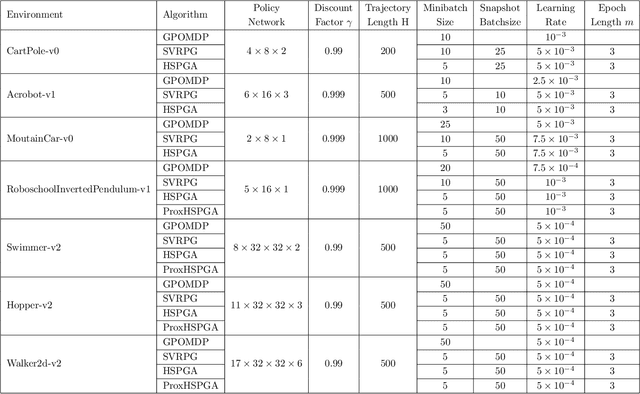
Abstract:We propose a novel hybrid stochastic policy gradient estimator by combining an unbiased policy gradient estimator, the REINFORCE estimator, with another biased one, an adapted SARAH estimator for policy optimization. The hybrid policy gradient estimator is shown to be biased, but has variance reduced property. Using this estimator, we develop a new Proximal Hybrid Stochastic Policy Gradient Algorithm (ProxHSPGA) to solve a composite policy optimization problem that allows us to handle constraints or regularizers on the policy parameters. We first propose a single-looped algorithm then introduce a more practical restarting variant. We prove that both algorithms can achieve the best-known trajectory complexity $\mathcal{O}\left(\varepsilon^{-3}\right)$ to attain a first-order stationary point for the composite problem which is better than existing REINFORCE/GPOMDP $\mathcal{O}\left(\varepsilon^{-4}\right)$ and SVRPG $\mathcal{O}\left(\varepsilon^{-10/3}\right)$ in the non-composite setting. We evaluate the performance of our algorithm on several well-known examples in reinforcement learning. Numerical results show that our algorithm outperforms two existing methods on these examples. Moreover, the composite settings indeed have some advantages compared to the non-composite ones on certain problems.
Stochastic Gauss-Newton Algorithms for Nonconvex Compositional Optimization
Feb 17, 2020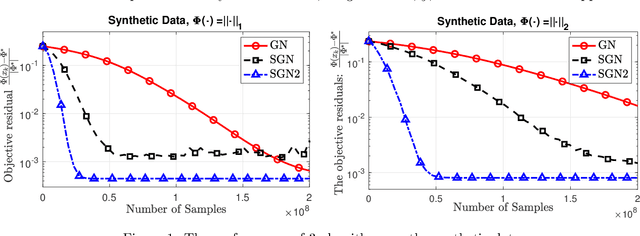
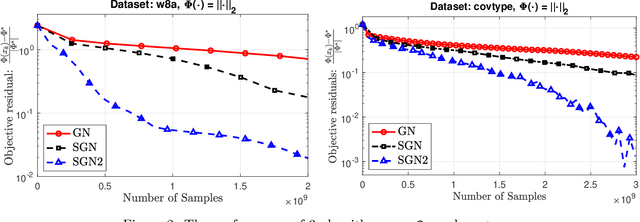
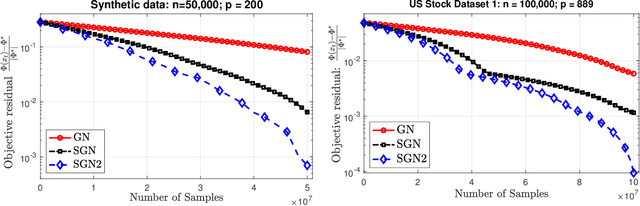
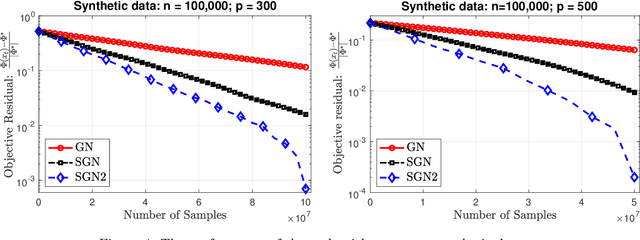
Abstract:We develop two new stochastic Gauss-Newton algorithms for solving a class of stochastic nonconvex compositional optimization problems frequently arising in practice. We consider both the expectation and finite-sum settings under standard assumptions. We use both classical stochastic and SARAH estimators for approximating function values and Jacobians. In the expectation case, we establish $\mathcal{O}(\varepsilon^{-2})$ iteration complexity to achieve a stationary point in expectation and estimate the total number of stochastic oracle calls for both function values and its Jacobian, where $\varepsilon$ is a desired accuracy. In the finite sum case, we also estimate the same iteration complexity and the total oracle calls with high probability. To our best knowledge, this is the first time such global stochastic oracle complexity is established for stochastic Gauss-Newton methods. We illustrate our theoretical results via numerical examples on both synthetic and real datasets.
A Hybrid Stochastic Optimization Framework for Stochastic Composite Nonconvex Optimization
Jul 08, 2019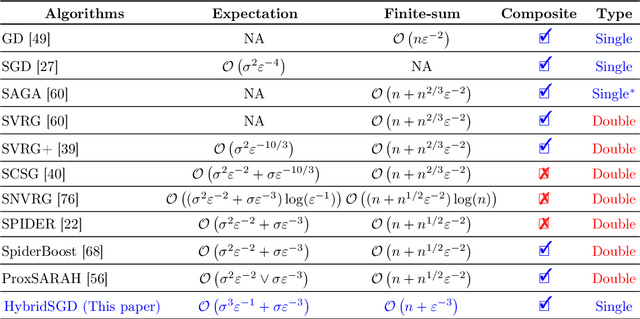
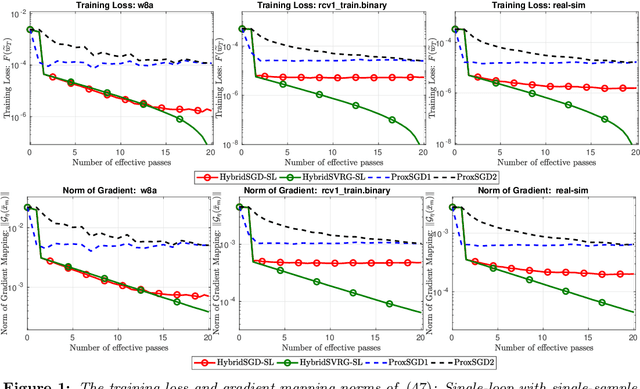
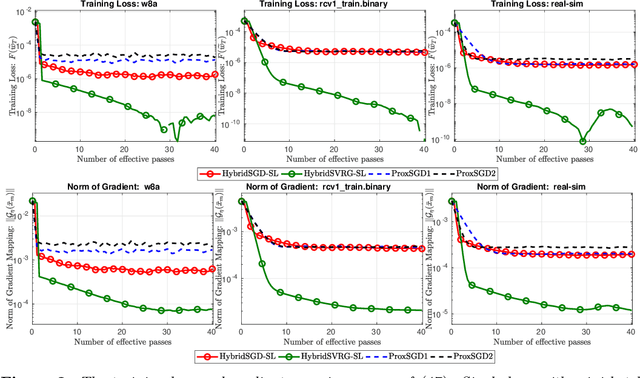
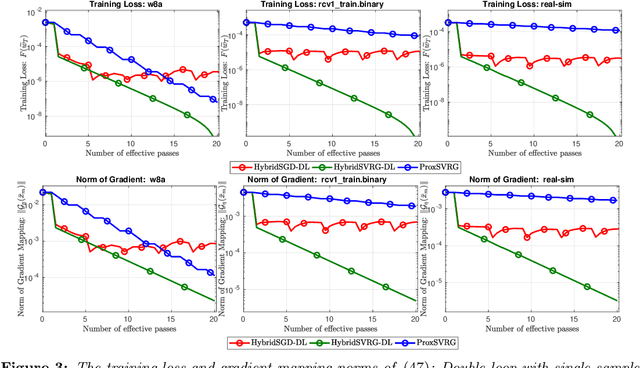
Abstract:In this paper, we introduce a new approach to develop stochastic optimization algorithms for solving stochastic composite and possibly nonconvex optimization problems. The main idea is to combine two stochastic estimators to form a new hybrid one. We first introduce our hybrid estimator and then investigate its fundamental properties to form a foundation theory for algorithmic development. Next, we apply our theory to develop several variants of stochastic gradient methods to solve both expectation and finite-sum composite optimization problems. Our first algorithm can be viewed as a variant of proximal stochastic gradient methods with a single-loop, but can achieve $\mathcal{O}(\sigma^3\varepsilon^{-1} + \sigma\varepsilon^{-3})$ complexity bound that is significantly better than the $\mathcal{O}(\sigma^2\varepsilon^{-4})$-complexity in state-of-the-art stochastic gradient methods, where $\sigma$ is the variance and $\varepsilon$ is a desired accuracy. Then, we consider two different variants of our method: adaptive step-size and double-loop schemes that have the same theoretical guarantees as in our first algorithm. We also study two mini-batch variants and develop two hybrid SARAH-SVRG algorithms to solve the finite-sum problems. In all cases, we achieve the best-known complexity bounds under standard assumptions. We test our methods on several numerical examples with real datasets and compare them with state-of-the-arts. Our numerical experiments show that the new methods are comparable and, in many cases, outperform their competitors.
Hybrid Stochastic Gradient Descent Algorithms for Stochastic Nonconvex Optimization
May 15, 2019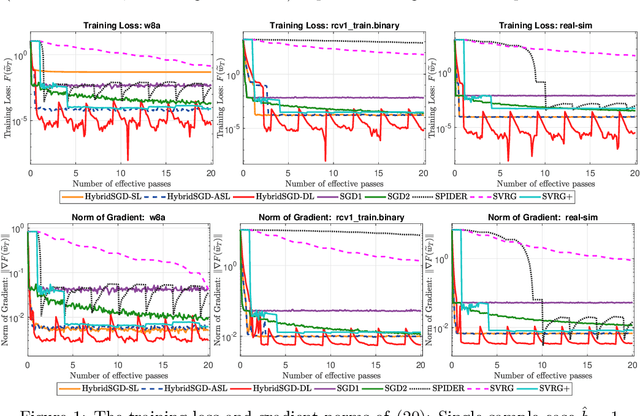
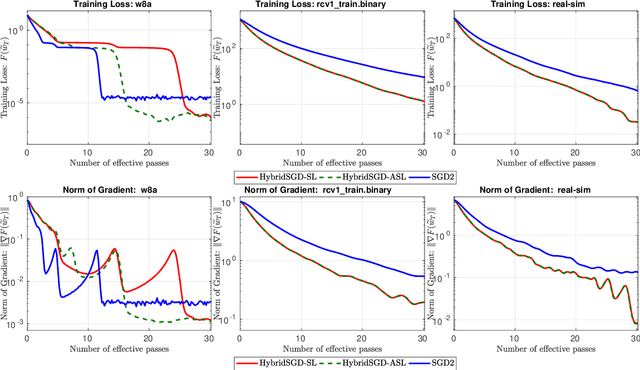
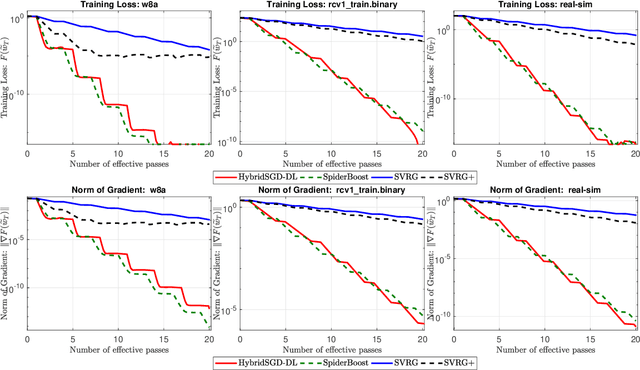
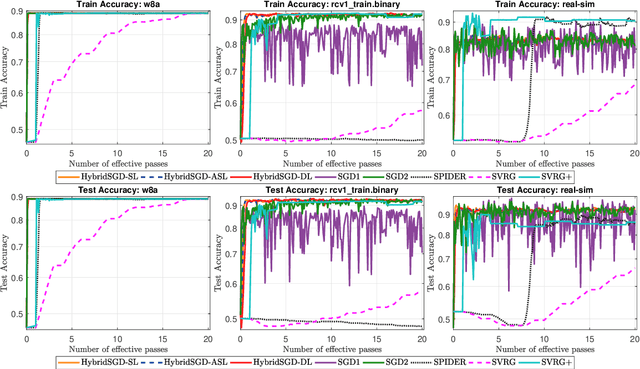
Abstract:We introduce a hybrid stochastic estimator to design stochastic gradient algorithms for solving stochastic optimization problems. Such a hybrid estimator is a convex combination of two existing biased and unbiased estimators and leads to some useful property on its variance. We limit our consideration to a hybrid SARAH-SGD for nonconvex expectation problems. However, our idea can be extended to handle a broader class of estimators in both convex and nonconvex settings. We propose a new single-loop stochastic gradient descent algorithm that can achieve $O(\max\{\sigma^3\varepsilon^{-1},\sigma\varepsilon^{-3}\})$-complexity bound to obtain an $\varepsilon$-stationary point under smoothness and $\sigma^2$-bounded variance assumptions. This complexity is better than $O(\sigma^2\varepsilon^{-4})$ often obtained in state-of-the-art SGDs when $\sigma < O(\varepsilon^{-3})$. We also consider different extensions of our method, including constant and adaptive step-size with single-loop, double-loop, and mini-batch variants. We compare our algorithms with existing methods on several datasets using two nonconvex models.
ProxSARAH: An Efficient Algorithmic Framework for Stochastic Composite Nonconvex Optimization
Mar 29, 2019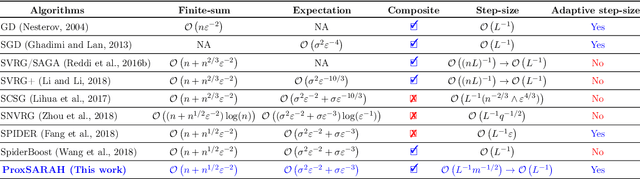
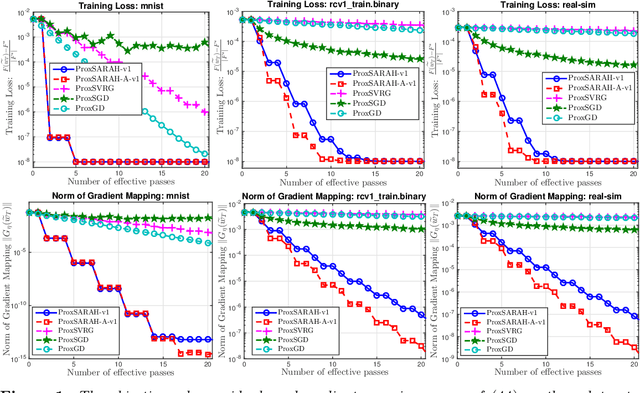
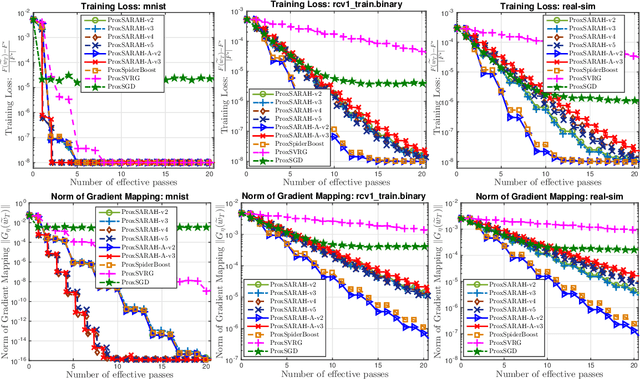
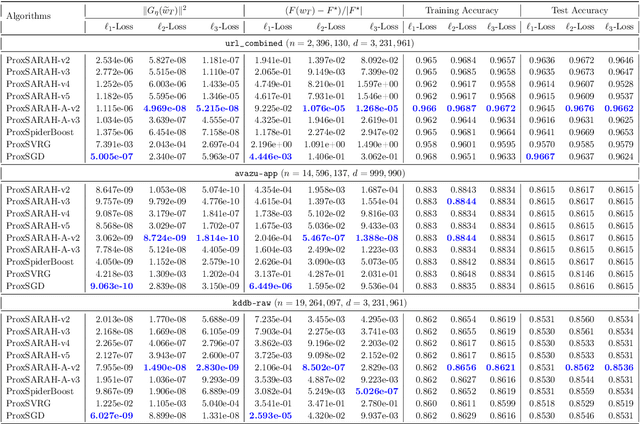
Abstract:We propose a new stochastic first-order algorithmic framework to solve stochastic composite nonconvex optimization problems that covers both finite-sum and expectation settings. Our algorithms rely on the SARAH estimator introduced in (Nguyen et al, 2017) and consist of two steps: a proximal gradient and an averaging step making them different from existing nonconvex proximal-type algorithms. The algorithms only require an average smoothness assumption of the nonconvex objective term and additional bounded variance assumption if applied to expectation problems. They work with both constant and adaptive step-sizes, while allowing single sample and mini-batches. In all these cases, we prove that our algorithms can achieve the best-known complexity bounds. One key step of our methods is new constant and adaptive step-sizes that help to achieve desired complexity bounds while improving practical performance. Our constant step-size is much larger than existing methods including proximal SVRG schemes in the single sample case. We also specify the algorithm to the non-composite case that covers existing state-of-the-arts in terms of complexity bounds. Our update also allows one to trade-off between step-sizes and mini-batch sizes to improve performance. We test the proposed algorithms on two composite nonconvex problems and neural networks using several well-known datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge