Graph Neural Networks and Applied Linear Algebra

Sparse matrix computations are ubiquitous in scientific computing. With the recent interest in scientific machine learning, it is natural to ask how sparse matrix computations can leverage neural networks (NN). Unfortunately, multi-layer perceptron (MLP) neural networks are typically not natural for either graph or sparse matrix computations. The issue lies with the fact that MLPs require fixed-sized inputs while scientific applications generally generate sparse matrices with arbitrary dimensions and a wide range of nonzero patterns (or matrix graph vertex interconnections). While convolutional NNs could possibly address matrix graphs where all vertices have the same number of nearest neighbors, a more general approach is needed for arbitrary sparse matrices, e.g. arising from discretized partial differential equations on unstructured meshes. Graph neural networks (GNNs) are one approach suitable to sparse matrices. GNNs define aggregation functions (e.g., summations) that operate on variable size input data to produce data of a fixed output size so that MLPs can be applied. The goal of this paper is to provide an introduction to GNNs for a numerical linear algebra audience. Concrete examples are provided to illustrate how many common linear algebra tasks can be accomplished using GNNs. We focus on iterative methods that employ computational kernels such as matrix-vector products, interpolation, relaxation methods, and strength-of-connection measures. Our GNN examples include cases where parameters are determined a-priori as well as cases where parameters must be learned. The intent with this article is to help computational scientists understand how GNNs can be used to adapt machine learning concepts to computational tasks associated with sparse matrices. It is hoped that this understanding will stimulate data-driven extensions of classical sparse linear algebra tasks.

Parallel Training of GRU Networks with a Multi-Grid Solver for Long Sequences

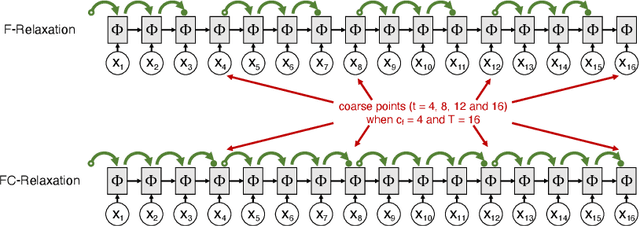
Parallelizing Gated Recurrent Unit (GRU) networks is a challenging task, as the training procedure of GRU is inherently sequential. Prior efforts to parallelize GRU have largely focused on conventional parallelization strategies such as data-parallel and model-parallel training algorithms. However, when the given sequences are very long, existing approaches are still inevitably performance limited in terms of training time. In this paper, we present a novel parallel training scheme (called parallel-in-time) for GRU based on a multigrid reduction in time (MGRIT) solver. MGRIT partitions a sequence into multiple shorter sub-sequences and trains the sub-sequences on different processors in parallel. The key to achieving speedup is a hierarchical correction of the hidden state to accelerate end-to-end communication in both the forward and backward propagation phases of gradient descent. Experimental results on the HMDB51 dataset, where each video is an image sequence, demonstrate that the new parallel training scheme achieves up to 6.5$\times$ speedup over a serial approach. As efficiency of our new parallelization strategy is associated with the sequence length, our parallel GRU algorithm achieves significant performance improvement as the sequence length increases.

Partition of unity networks: deep hp-approximation

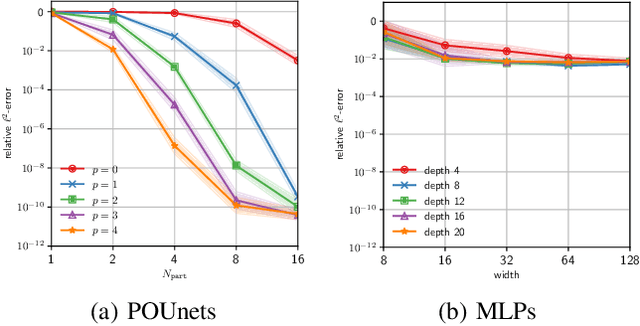
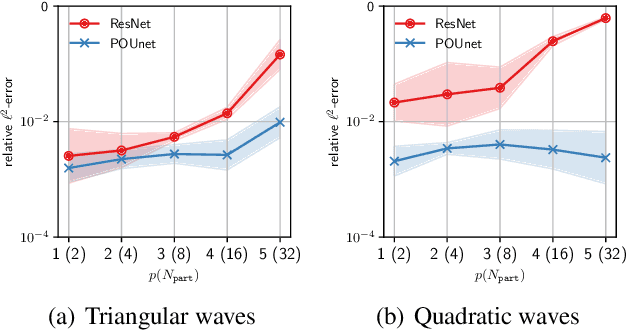
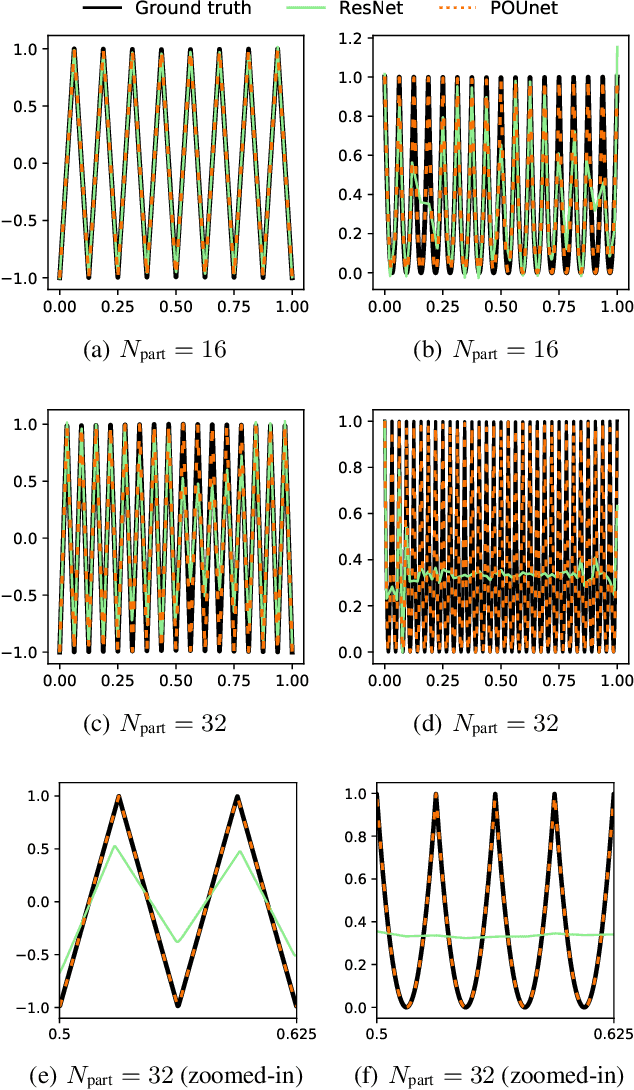
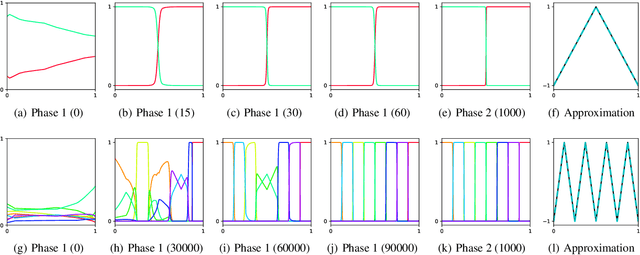
Approximation theorists have established best-in-class optimal approximation rates of deep neural networks by utilizing their ability to simultaneously emulate partitions of unity and monomials. Motivated by this, we propose partition of unity networks (POUnets) which incorporate these elements directly into the architecture. Classification architectures of the type used to learn probability measures are used to build a meshfree partition of space, while polynomial spaces with learnable coefficients are associated to each partition. The resulting hp-element-like approximation allows use of a fast least-squares optimizer, and the resulting architecture size need not scale exponentially with spatial dimension, breaking the curse of dimensionality. An abstract approximation result establishes desirable properties to guide network design. Numerical results for two choices of architecture demonstrate that POUnets yield hp-convergence for smooth functions and consistently outperform MLPs for piecewise polynomial functions with large numbers of discontinuities.

A physics-informed operator regression framework for extracting data-driven continuum models

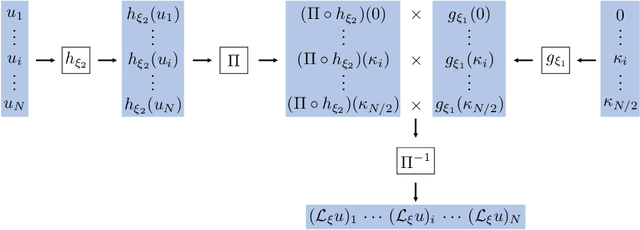
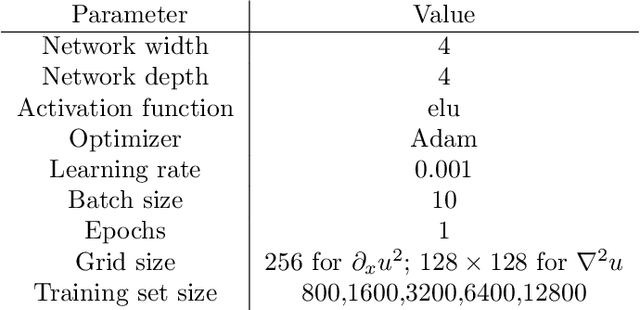
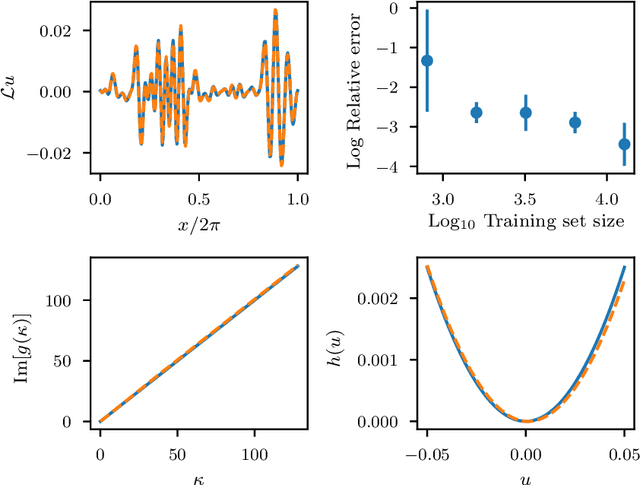
The application of deep learning toward discovery of data-driven models requires careful application of inductive biases to obtain a description of physics which is both accurate and robust. We present here a framework for discovering continuum models from high fidelity molecular simulation data. Our approach applies a neural network parameterization of governing physics in modal space, allowing a characterization of differential operators while providing structure which may be used to impose biases related to symmetry, isotropy, and conservation form. We demonstrate the effectiveness of our framework for a variety of physics, including local and nonlocal diffusion processes and single and multiphase flows. For the flow physics we demonstrate this approach leads to a learned operator that generalizes to system characteristics not included in the training sets, such as variable particle sizes, densities, and concentration.

A block coordinate descent optimizer for classification problems exploiting convexity

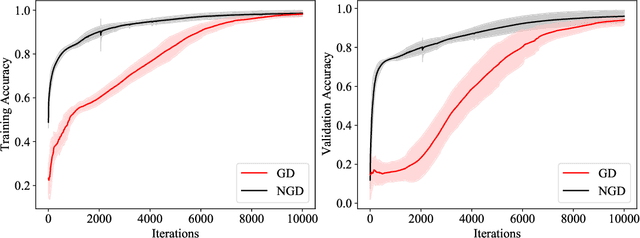
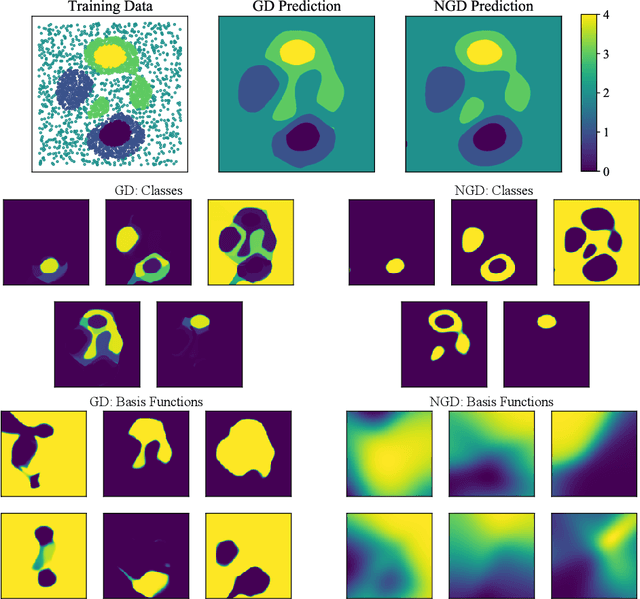
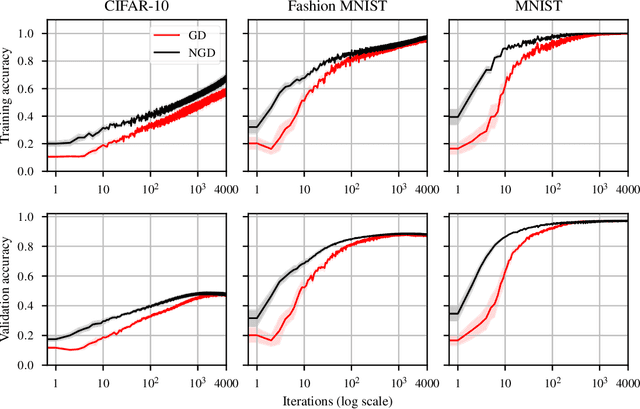
Second-order optimizers hold intriguing potential for deep learning, but suffer from increased cost and sensitivity to the non-convexity of the loss surface as compared to gradient-based approaches. We introduce a coordinate descent method to train deep neural networks for classification tasks that exploits global convexity of the cross-entropy loss in the weights of the linear layer. Our hybrid Newton/Gradient Descent (NGD) method is consistent with the interpretation of hidden layers as providing an adaptive basis and the linear layer as providing an optimal fit of the basis to data. By alternating between a second-order method to find globally optimal parameters for the linear layer and gradient descent to train the hidden layers, we ensure an optimal fit of the adaptive basis to data throughout training. The size of the Hessian in the second-order step scales only with the number weights in the linear layer and not the depth and width of the hidden layers; furthermore, the approach is applicable to arbitrary hidden layer architecture. Previous work applying this adaptive basis perspective to regression problems demonstrated significant improvements in accuracy at reduced training cost, and this work can be viewed as an extension of this approach to classification problems. We first prove that the resulting Hessian matrix is symmetric semi-definite, and that the Newton step realizes a global minimizer. By studying classification of manufactured two-dimensional point cloud data, we demonstrate both an improvement in validation error and a striking qualitative difference in the basis functions encoded in the hidden layer when trained using NGD. Application to image classification benchmarks for both dense and convolutional architectures reveals improved training accuracy, suggesting possible gains of second-order methods over gradient descent.

Multilevel Initialization for Layer-Parallel Deep Neural Network Training

This paper investigates multilevel initialization strategies for training very deep neural networks with a layer-parallel multigrid solver. The scheme is based on the continuous interpretation of the training problem as a problem of optimal control, in which neural networks are represented as discretizations of time-dependent ordinary differential equations. A key goal is to develop a method able to intelligently initialize the network parameters for the very deep networks enabled by scalable layer-parallel training. To do this, we apply a refinement strategy across the time domain, that is equivalent to refining in the layer dimension. The resulting refinements create deep networks, with good initializations for the network parameters coming from the coarser trained networks. We investigate the effectiveness of such multilevel "nested iteration" strategies for network training, showing supporting numerical evidence of reduced run time for equivalent accuracy. In addition, we study whether the initialization strategies provide a regularizing effect on the overall training process and reduce sensitivity to hyperparameters and randomness in initial network parameters.

Robust Training and Initialization of Deep Neural Networks: An Adaptive Basis Viewpoint

Motivated by the gap between theoretical optimal approximation rates of deep neural networks (DNNs) and the accuracy realized in practice, we seek to improve the training of DNNs. The adoption of an adaptive basis viewpoint of DNNs leads to novel initializations and a hybrid least squares/gradient descent optimizer. We provide analysis of these techniques and illustrate via numerical examples dramatic increases in accuracy and convergence rate for benchmarks characterizing scientific applications where DNNs are currently used, including regression problems and physics-informed neural networks for the solution of partial differential equations.