TimeAutoDiff: Combining Autoencoder and Diffusion model for time series tabular data synthesizing

In this paper, we leverage the power of latent diffusion models to generate synthetic time series tabular data. Along with the temporal and feature correlations, the heterogeneous nature of the feature in the table has been one of the main obstacles in time series tabular data modeling. We tackle this problem by combining the ideas of the variational auto-encoder (VAE) and the denoising diffusion probabilistic model (DDPM). Our model named as \texttt{TimeAutoDiff} has several key advantages including (1) Generality: the ability to handle the broad spectrum of time series tabular data from single to multi-sequence datasets; (2) Good fidelity and utility guarantees: numerical experiments on six publicly available datasets demonstrating significant improvements over state-of-the-art models in generating time series tabular data, across four metrics measuring fidelity and utility; (3) Fast sampling speed: entire time series data generation as opposed to the sequential data sampling schemes implemented in the existing diffusion-based models, eventually leading to significant improvements in sampling speed, (4) Entity conditional generation: the first implementation of conditional generation of multi-sequence time series tabular data with heterogenous features in the literature, enabling scenario exploration across multiple scientific and engineering domains. Codes are in preparation for release to the public, but available upon request.

Discriminative Estimation of Total Variation Distance: A Fidelity Auditor for Generative Data

With the proliferation of generative AI and the increasing volume of generative data (also called as synthetic data), assessing the fidelity of generative data has become a critical concern. In this paper, we propose a discriminative approach to estimate the total variation (TV) distance between two distributions as an effective measure of generative data fidelity. Our method quantitatively characterizes the relation between the Bayes risk in classifying two distributions and their TV distance. Therefore, the estimation of total variation distance reduces to that of the Bayes risk. In particular, this paper establishes theoretical results regarding the convergence rate of the estimation error of TV distance between two Gaussian distributions. We demonstrate that, with a specific choice of hypothesis class in classification, a fast convergence rate in estimating the TV distance can be achieved. Specifically, the estimation accuracy of the TV distance is proven to inherently depend on the separation of two Gaussian distributions: smaller estimation errors are achieved when the two Gaussian distributions are farther apart. This phenomenon is also validated empirically through extensive simulations. In the end, we apply this discriminative estimation method to rank fidelity of synthetic image data using the MNIST dataset.

Approximation of RKHS Functionals by Neural Networks

Motivated by the abundance of functional data such as time series and images, there has been a growing interest in integrating such data into neural networks and learning maps from function spaces to R (i.e., functionals). In this paper, we study the approximation of functionals on reproducing kernel Hilbert spaces (RKHS's) using neural networks. We establish the universality of the approximation of functionals on the RKHS's. Specifically, we derive explicit error bounds for those induced by inverse multiquadric, Gaussian, and Sobolev kernels. Moreover, we apply our findings to functional regression, proving that neural networks can accurately approximate the regression maps in generalized functional linear models. Existing works on functional learning require integration-type basis function expansions with a set of pre-specified basis functions. By leveraging the interpolating orthogonal projections in RKHS's, our proposed network is much simpler in that we use point evaluations to replace basis function expansions.

Benefits of Transformer: In-Context Learning in Linear Regression Tasks with Unstructured Data

In practice, it is observed that transformer-based models can learn concepts in context in the inference stage. While existing literature, e.g., \citet{zhang2023trained,huang2023context}, provide theoretical explanations on this in-context learning ability, they assume the input $x_i$ and the output $y_i$ for each sample are embedded in the same token (i.e., structured data). However, in reality, they are presented in two tokens (i.e., unstructured data \cite{wibisono2023role}). In this case, this paper conducts experiments in linear regression tasks to study the benefits of the architecture of transformers and provides some corresponding theoretical intuitions to explain why the transformer can learn from unstructured data. We study the exact components in a transformer that facilitate the in-context learning. In particular, we observe that (1) a transformer with two layers of softmax (self-)attentions with look-ahead attention mask can learn from the prompt if $y_i$ is in the token next to $x_i$ for each example; (2) positional encoding can further improve the performance; and (3) multi-head attention with a high input embedding dimension has a better prediction performance than single-head attention.

A Survey on Statistical Theory of Deep Learning: Approximation, Training Dynamics, and Generative Models

In this article, we review the literature on statistical theories of neural networks from three perspectives. In the first part, results on excess risks for neural networks are reviewed in the nonparametric framework of regression or classification. These results rely on explicit constructions of neural networks, leading to fast convergence rates of excess risks, in that tools from the approximation theory are adopted. Through these constructions, the width and depth of the networks can be expressed in terms of sample size, data dimension, and function smoothness. Nonetheless, their underlying analysis only applies to the global minimizer in the highly non-convex landscape of deep neural networks. This motivates us to review the training dynamics of neural networks in the second part. Specifically, we review papers that attempt to answer ``how the neural network trained via gradient-based methods finds the solution that can generalize well on unseen data.'' In particular, two well-known paradigms are reviewed: the Neural Tangent Kernel (NTK) paradigm, and Mean-Field (MF) paradigm. In the last part, we review the most recent theoretical advancements in generative models including Generative Adversarial Networks (GANs), diffusion models, and in-context learning (ICL) in the Large Language Models (LLMs). The former two models are known to be the main pillars of the modern generative AI era, while ICL is a strong capability of LLMs in learning from a few examples in the context. Finally, we conclude the paper by suggesting several promising directions for deep learning theory.

AutoDiff: combining Auto-encoder and Diffusion model for tabular data synthesizing

Diffusion model has become a main paradigm for synthetic data generation in many subfields of modern machine learning, including computer vision, language model, or speech synthesis. In this paper, we leverage the power of diffusion model for generating synthetic tabular data. The heterogeneous features in tabular data have been main obstacles in tabular data synthesis, and we tackle this problem by employing the auto-encoder architecture. When compared with the state-of-the-art tabular synthesizers, the resulting synthetic tables from our model show nice statistical fidelities to the real data, and perform well in downstream tasks for machine learning utilities. We conducted the experiments over 15 publicly available datasets. Notably, our model adeptly captures the correlations among features, which has been a long-standing challenge in tabular data synthesis. Our code is available upon request and will be publicly released if paper is accepted.

On Excess Risk Convergence Rates of Neural Network Classifiers

The recent success of neural networks in pattern recognition and classification problems suggests that neural networks possess qualities distinct from other more classical classifiers such as SVMs or boosting classifiers. This paper studies the performance of plug-in classifiers based on neural networks in a binary classification setting as measured by their excess risks. Compared to the typical settings imposed in the literature, we consider a more general scenario that resembles actual practice in two respects: first, the function class to be approximated includes the Barron functions as a proper subset, and second, the neural network classifier constructed is the minimizer of a surrogate loss instead of the $0$-$1$ loss so that gradient descent-based numerical optimizations can be easily applied. While the class of functions we consider is quite large that optimal rates cannot be faster than $n^{-\frac{1}{3}}$, it is a regime in which dimension-free rates are possible and approximation power of neural networks can be taken advantage of. In particular, we analyze the estimation and approximation properties of neural networks to obtain a dimension-free, uniform rate of convergence for the excess risk. Finally, we show that the rate obtained is in fact minimax optimal up to a logarithmic factor, and the minimax lower bound shows the effect of the margin assumption in this regime.

Asymptotic Theory of $\ell_1$-Regularized PDE Identification from a Single Noisy Trajectory

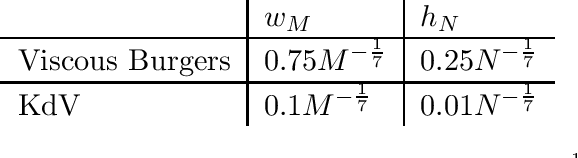
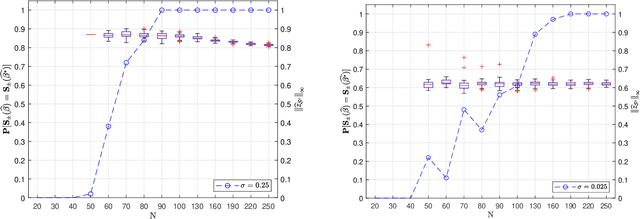
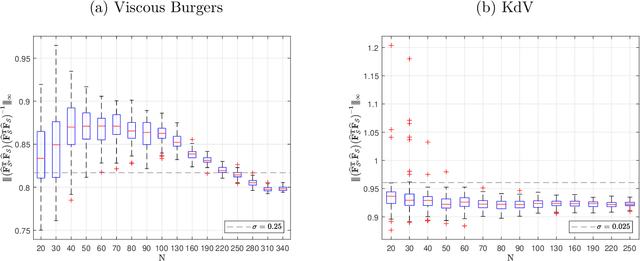
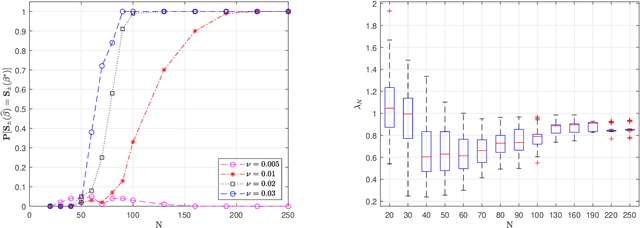
We prove the support recovery for a general class of linear and nonlinear evolutionary partial differential equation (PDE) identification from a single noisy trajectory using $\ell_1$ regularized Pseudo-Least Squares model~($\ell_1$-PsLS). In any associative $\mathbb{R}$-algebra generated by finitely many differentiation operators that contain the unknown PDE operator, applying $\ell_1$-PsLS to a given data set yields a family of candidate models with coefficients $\mathbf{c}(\lambda)$ parameterized by the regularization weight $\lambda\geq 0$. The trace of $\{\mathbf{c}(\lambda)\}_{\lambda\geq 0}$ suffers from high variance due to data noises and finite difference approximation errors. We provide a set of sufficient conditions which guarantee that, from a single trajectory data denoised by a Local-Polynomial filter, the support of $\mathbf{c}(\lambda)$ asymptotically converges to the true signed-support associated with the underlying PDE for sufficiently many data and a certain range of $\lambda$. We also show various numerical experiments to validate our theory.

Factor Analysis on Citation, Using a Combined Latent and Logistic Regression Model

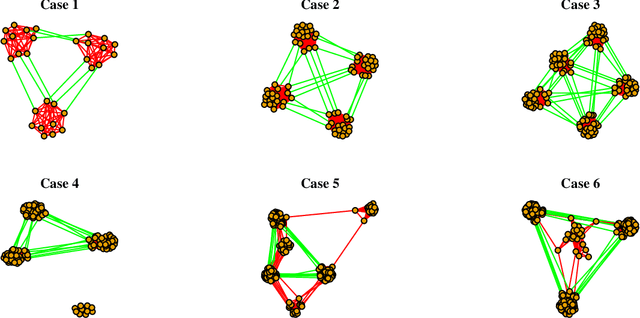
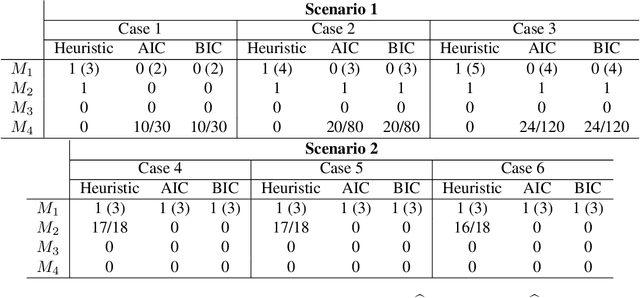
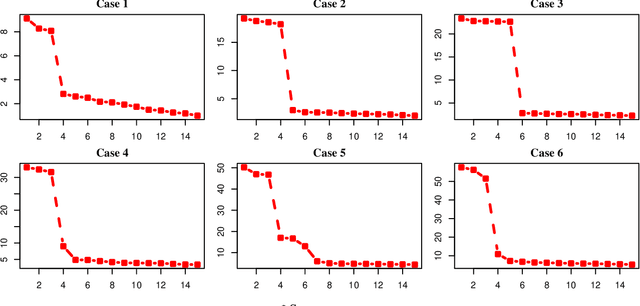
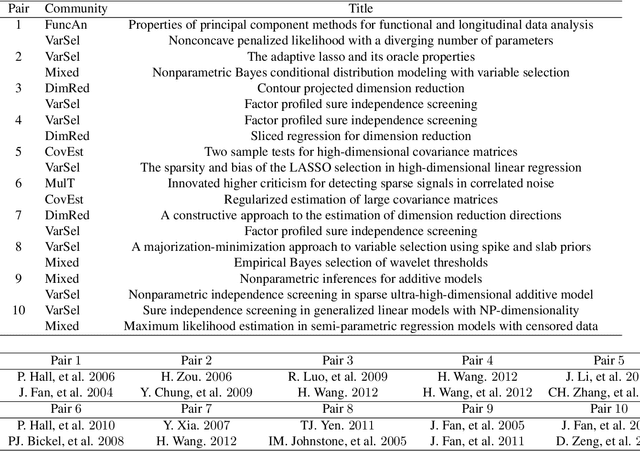
We propose a combined model, which integrates the latent factor model and the logistic regression model, for the citation network. It is noticed that neither a latent factor model nor a logistic regression model alone is sufficient to capture the structure of the data. The proposed model has a latent (i.e., factor analysis) model to represents the main technological trends (a.k.a., factors), and adds a sparse component that captures the remaining ad-hoc dependence. Parameter estimation is carried out through the construction of a joint-likelihood function of edges and properly chosen penalty terms. The convexity of the objective function allows us to develop an efficient algorithm, while the penalty terms push towards a low-dimensional latent component and a sparse graphical structure. Simulation results show that the proposed method works well in practical situations. The proposed method has been applied to a real application, which contains a citation network of statisticians (Ji and Jin, 2016). Some interesting findings are reported.

Review on Parameter Estimation in HMRF

This is a technical report which explores the estimation methodologies on hyper-parameters in Markov Random Field and Gaussian Hidden Markov Random Field. In first section, we briefly investigate a theoretical framework on Metropolis-Hastings algorithm. Next, by using MH algorithm, we simulate the data from Ising model, and study on how hyper-parameter estimation in Ising model is enabled through MCMC algorithm using pseudo-likelihood approximation. Following section deals with an issue on parameters estimation process of Gaussian Hidden Markov Random Field using MAP estimation and EM algorithm, and also discusses problems, found through several experiments. In following section, we expand this idea on estimating parameters in Gaussian Hidden Markov Spatial-Temporal Random Field, and display results on two performed experiments.