Asymptotic Theory of $\ell_1$-Regularized PDE Identification from a Single Noisy Trajectory
Paper and Code
Mar 12, 2021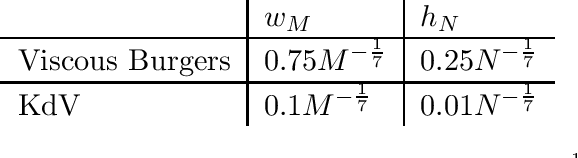
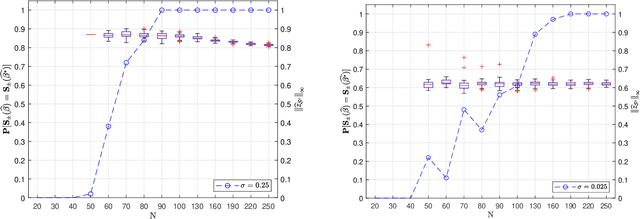
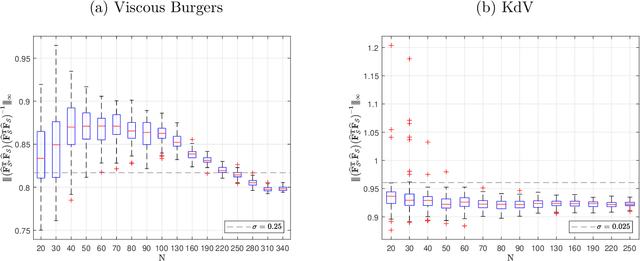
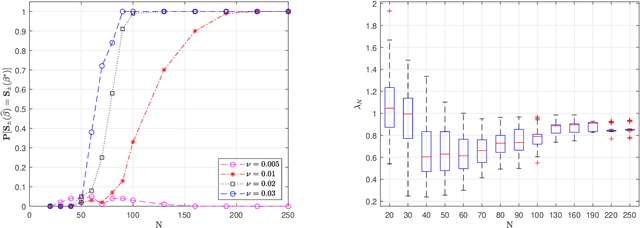
We prove the support recovery for a general class of linear and nonlinear evolutionary partial differential equation (PDE) identification from a single noisy trajectory using $\ell_1$ regularized Pseudo-Least Squares model~($\ell_1$-PsLS). In any associative $\mathbb{R}$-algebra generated by finitely many differentiation operators that contain the unknown PDE operator, applying $\ell_1$-PsLS to a given data set yields a family of candidate models with coefficients $\mathbf{c}(\lambda)$ parameterized by the regularization weight $\lambda\geq 0$. The trace of $\{\mathbf{c}(\lambda)\}_{\lambda\geq 0}$ suffers from high variance due to data noises and finite difference approximation errors. We provide a set of sufficient conditions which guarantee that, from a single trajectory data denoised by a Local-Polynomial filter, the support of $\mathbf{c}(\lambda)$ asymptotically converges to the true signed-support associated with the underlying PDE for sufficiently many data and a certain range of $\lambda$. We also show various numerical experiments to validate our theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge