Text-to-Distribution Prediction with Quantile Tokens and Neighbor Context

Many applications of LLM-based text regression require predicting a full conditional distribution rather than a single point value. We study distributional regression under empirical-quantile supervision, where each input is paired with multiple observed quantile outcomes, and the target distribution is represented by a dense grid of quantiles. We address two key limitations of current approaches: the lack of local grounding for distribution estimates, and the reliance on shared representations that create an indirect bottleneck between inputs and quantile outputs. In this paper, we introduce Quantile Token Regression, which, to our knowledge, is the first work to insert dedicated quantile tokens into the input sequence, enabling direct input-output pathways for each quantile through self-attention. We further augment these quantile tokens with retrieval, incorporating semantically similar neighbor instances and their empirical distributions to ground predictions with local evidence from similar instances. We also provide the first theoretical analysis of loss functions for quantile regression, clarifying which distributional objectives each optimizes. Experiments on the Inside Airbnb and StackSample benchmark datasets with LLMs ranging from 1.7B to 14B parameters show that quantile tokens with neighbors consistently outperform baselines (~4 points lower MAPE and 2x narrower prediction intervals), with especially large gains on smaller and more challenging datasets where quantile tokens produce substantially sharper and more accurate distributions.

Exploring Safety Alignment Evaluation of LLMs in Chinese Mental Health Dialogues via LLM-as-Judge

Evaluating the safety alignment of LLM responses in high-risk mental health dialogues is particularly difficult due to missing gold-standard answers and the ethically sensitive nature of these interactions. To address this challenge, we propose PsyCrisis-Bench, a reference-free evaluation benchmark based on real-world Chinese mental health dialogues. It evaluates whether the model responses align with the safety principles defined by experts. Specifically designed for settings without standard references, our method adopts a prompt-based LLM-as-Judge approach that conducts in-context evaluation using expert-defined reasoning chains grounded in psychological intervention principles. We employ binary point-wise scoring across multiple safety dimensions to enhance the explainability and traceability of the evaluation. Additionally, we present a manually curated, high-quality Chinese-language dataset covering self-harm, suicidal ideation, and existential distress, derived from real-world online discourse. Experiments on 3600 judgments show that our method achieves the highest agreement with expert assessments and produces more interpretable evaluation rationales compared to existing approaches. Our dataset and evaluation tool are publicly available to facilitate further research.

Hierarchical Conditional Semi-Paired Image-to-Image Translation For Multi-Task Image Defect Correction On Shopping Websites

On shopping websites, product images of low quality negatively affect customer experience. Although there are plenty of work in detecting images with different defects, few efforts have been dedicated to correct those defects at scale. A major challenge is that there are thousands of product types and each has specific defects, therefore building defect specific models is unscalable. In this paper, we propose a unified Image-to-Image (I2I) translation model to correct multiple defects across different product types. Our model leverages an attention mechanism to hierarchically incorporate high-level defect groups and specific defect types to guide the network to focus on defect-related image regions. Evaluated on eight public datasets, our model reduces the Frechet Inception Distance (FID) by 24.6% in average compared with MoNCE, the state-of-the-art I2I method. Unlike public data, another practical challenge on shopping websites is that some paired images are of low quality. Therefore we design our model to be semi-paired by combining the L1 loss of paired data with the cycle loss of unpaired data. Tested on a shopping website dataset to correct three image defects, our model reduces (FID) by 63.2% in average compared with WS-I2I, the state-of-the art semi-paired I2I method.

On Negative Transfer and Structure of Latent Functions in Multi-output Gaussian Processes

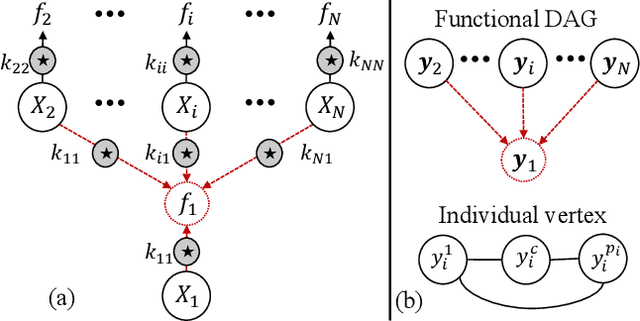
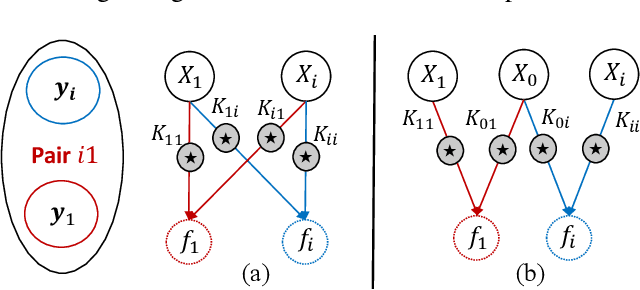
The multi-output Gaussian process ($\mathcal{MGP}$) is based on the assumption that outputs share commonalities, however, if this assumption does not hold negative transfer will lead to decreased performance relative to learning outputs independently or in subsets. In this article, we first define negative transfer in the context of an $\mathcal{MGP}$ and then derive necessary conditions for an $\mathcal{MGP}$ model to avoid negative transfer. Specifically, under the convolution construction, we show that avoiding negative transfer is mainly dependent on having a sufficient number of latent functions $Q$ regardless of the flexibility of the kernel or inference procedure used. However, a slight increase in $Q$ leads to a large increase in the number of parameters to be estimated. To this end, we propose two latent structures that scale to arbitrarily large datasets, can avoid negative transfer and allow any kernel or sparse approximations to be used within. These structures also allow regularization which can provide consistent and automatic selection of related outputs.