On the Achievable Rate of Satellite Quantum Communication Channel using Deep Autoencoder Gaussian Mixture Model

We present a comparative study of the Gaussian mixture model (GMM) and the Deep Autoencoder Gaussian Mixture Model (DAGMM) for estimating satellite quantum channel capacity, considering hybrid quantum noise (HQN) and transmission constraints. While GMM is simple and interpretable, DAGMM better captures non-linear variations and noise distributions. Simulations show that DAGMM provides tighter capacity bounds and improved clustering. This introduces the Deep Cluster Gaussian Mixture Model (DCGMM) for high-dimensional quantum data analysis in quantum satellite communication.

A Hybrid Noise Approach to Modelling of Free-Space Satellite Quantum Communication Channel for Continuous-Variable QKD

This paper significantly advances the application of Quantum Key Distribution (QKD) in Free- Space Optics (FSO) satellite-based quantum communication. We propose an innovative satellite quantum channel model and derive the secret quantum key distribution rate achievable through this channel. Unlike existing models that approximate the noise in quantum channels as merely Gaussian distributed, our model incorporates a hybrid noise analysis, accounting for both quantum Poissonian noise and classical Additive-White-Gaussian Noise (AWGN). This hybrid approach acknowledges the dual vulnerability of continuous variables (CV) Gaussian quantum channels to both quantum and classical noise, thereby offering a more realistic assessment of the quantum Secret Key Rate (SKR). This paper delves into the variation of SKR with the Signal-to-Noise Ratio (SNR) under various influencing parameters. We identify and analyze critical factors such as reconciliation efficiency, transmission coefficient, transmission efficiency, the quantum Poissonian noise parameter, and the satellite altitude. These parameters are pivotal in determining the SKR in FSO satellite quantum channels, highlighting the challenges of satellitebased quantum communication. Our work provides a comprehensive framework for understanding and optimizing SKR in satellite-based QKD systems, paving the way for more efficient and secure quantum communication networks.

Hybrid Quantum Noise Approximation and Pattern Analysis on Parameterized Component Distributions

Noise is a vital factor in determining the accuracy of processing the information of the quantum channel. One must consider classical noise effects associated with quantum noise sources for more realistic modelling of quantum channels. A hybrid quantum noise model incorporating both quantum Poisson noise and classical additive white Gaussian noise (AWGN) can be interpreted as an infinite mixture of Gaussians with weightage from the Poisson distribution. The entropy measure of this function is difficult to calculate. This research developed how the infinite mixture can be well approximated by a finite mixture distribution depending on the Poisson parametric setting compared to the number of mixture components. The mathematical analysis of the characterization of hybrid quantum noise has been demonstrated based on Gaussian and Poisson parametric analysis. This helps in the pattern analysis of the parametric values of the component distribution, and it also helps in the calculation of hybrid noise entropy to understand hybrid quantum noise better.

A Machine Learning Approach for Optimizing Hybrid Quantum Noise Clusters for Gaussian Quantum Channel Capacity

This work contributes to the advancement of quantum communication by visualizing hybrid quantum noise in higher dimensions and optimizing the capacity of the quantum channel by using machine learning (ML). Employing the expectation maximization (EM) algorithm, the quantum channel parameters are iteratively adjusted to estimate the channel capacity, facilitating the categorization of quantum noise data in higher dimensions into a finite number of clusters. In contrast to previous investigations that represented the model in lower dimensions, our work describes the quantum noise as a Gaussian Mixture Model (GMM) with mixing weights derived from a Poisson distribution. The objective was to model the quantum noise using a finite mixture of Gaussian components while preserving the mixing coefficients from the Poisson distribution. Approximating the infinite Gaussian mixture with a finite number of components makes it feasible to visualize clusters of quantum noise data without modifying the original probability density function. By implementing the EM algorithm, the research fine-tuned the channel parameters, identified optimal clusters, improved channel capacity estimation, and offered insights into the characteristics of quantum noise within an ML framework.

Quantum Channel Modelling by Statistical Quantum Signal Processing

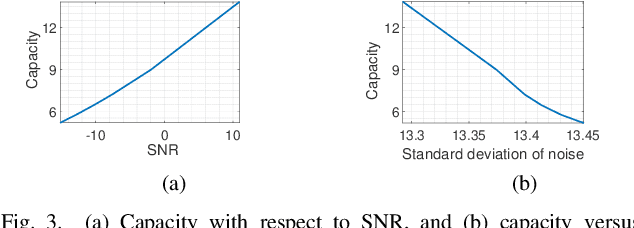
In this paper we are interested to model quantum signal by statistical signal processing methods. The Gaussian distribution has been considered for the input quantum signal as Gaussian state have been proven to a type of important robust state and most of the important experiments of quantum information are done with Gaussian light. Along with that a joint noise model has been invoked, and followed by a received signal model has been formulated by using convolution of transmitted signal and joint quantum noise to realized theoretical achievable capacity of the single quantum link. In joint quantum noise model we consider the quantum Poisson noise with classical Gaussian noise. We compare the capacity of the quantum channel with respect to SNR to detect its overall tendency. In this paper we use the channel equation in terms of random variable to investigate the quantum signals and noise model statistically. These methods are proposed to develop Quantum statistical signal processing and the idea comes from the statistical signal processing.

Mathematical Model of Quantum Channel Capacity

In this article, we are proposing a closed-form solution for the capacity of the single quantum channel. The Gaussian distributed input has been considered for the analytical calculation of the capacity. In our previous couple of papers, we invoked models for joint quantum noise and the corresponding received signals; in this current research, we proved that these models are Gaussian mixtures distributions. In this paper, we showed how to deal with both of cases, namely (I)the Gaussian mixtures distribution for scalar variables and (II) the Gaussian mixtures distribution for random vectors. Our target is to calculate the entropy of the joint noise and the entropy of the received signal in order to calculate the capacity expression of the quantum channel. The main challenge is to work with the function type of the Gaussian mixture distribution. The entropy of the Gaussian mixture distributions cannot be calculated in the closed-form solution due to the logarithm of a sum of exponential functions. As a solution, we proposed a lower bound and a upper bound for each of the entropies of joint noise and the received signal, and finally upper inequality and lower inequality lead to the upper bound for the mutual information and hence the maximum achievable data rate as the capacity. In this paper reader will able to visualize an closed-form capacity experssion which make this paper distinct from our previous works. These capacity experssion and coresses ponding bounds are calculated for both the cases: the Gaussian mixtures distribution for scalar variables and the Gaussian mixtures distribution for random vectors as well.

Joint Modelling of Quantum and Classical Noise over Unity Quantum Channel

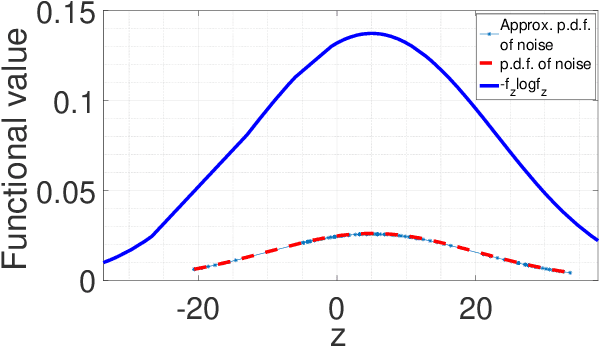
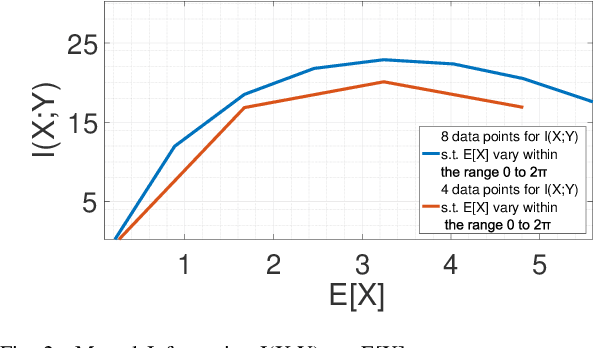
For a continuous-input-continuous-output arbitrarily distributed quantum channel carrying classical information, the channel capacity can be computed in terms of the distribution of the channel envelope, received signal strength over a quantum propagation field and the noise spectral density. If the channel envelope is considered to be unity with unit received signal strength, the factor controlling the capacity is the noise. Quantum channel carrying classical information will suffer from the combination of classical and quantum noise. Assuming additive Gaussian-distributed classical noise and Poisson-distributed quantum noise, we formulate a hybrid noise model by deriving a joint Gaussian- Poisson distribution in this letter. For the transmitted signal, we consider the mean of signal sample space instead of considering a particular distribution and study how the maximum mutual information varies over such mean value. Capacity is estimated by maximizing the mutual information over unity channel envelope.