An Overview of zbMATH Open Digital Library

Mathematical research thrives on the effective dissemination and discovery of knowledge. zbMATH Open has emerged as a pivotal platform in this landscape, offering a comprehensive repository of mathematical literature. Beyond indexing and abstracting, it serves as a unified quality-assured infrastructure for finding, evaluating, and connecting mathematical information that advances mathematical research as well as interdisciplinary exploration. zbMATH Open enables scientific quality control by post-publication reviews and promotes connections between researchers, institutions, and research outputs. This paper represents the functionalities of the most significant features of this open-access service, highlighting its role in shaping the future of mathematical information retrieval.

Reducing the climate impact of data portals: a case study

The carbon footprint share of the information and communication technology (ICT) sector has steadily increased in the past decade and is predicted to make up as much as 23 \% of global emissions in 2030. This shows a pressing need for developers, including the information retrieval community, to make their code more energy-efficient. In this project proposal, we discuss techniques to reduce the energy footprint of the MaRDI (Mathematical Research Data Initiative) Portal, a MediaWiki-based knowledge base. In future work, we plan to implement these changes and provide concrete measurements on the gain in energy efficiency. Researchers developing similar knowledge bases can adapt our measures to reduce their environmental footprint. In this way, we are working on mitigating the climate impact of Information Retrieval research.

Can LLMs Master Math? Investigating Large Language Models on Math Stack Exchange

Large Language Models (LLMs) have demonstrated exceptional capabilities in various natural language tasks, often achieving performances that surpass those of humans. Despite these advancements, the domain of mathematics presents a distinctive challenge, primarily due to its specialized structure and the precision it demands. In this study, we adopted a two-step approach for investigating the proficiency of LLMs in answering mathematical questions. First, we employ the most effective LLMs, as identified by their performance on math question-answer benchmarks, to generate answers to 78 questions from the Math Stack Exchange (MSE). Second, a case analysis is conducted on the LLM that showed the highest performance, focusing on the quality and accuracy of its answers through manual evaluation. We found that GPT-4 performs best (nDCG of 0.48 and P@10 of 0.37) amongst existing LLMs fine-tuned for answering mathematics questions and outperforms the current best approach on ArqMATH3 Task1, considering P@10. Our Case analysis indicates that while the GPT-4 can generate relevant responses in certain instances, it does not consistently answer all questions accurately. This paper explores the current limitations of LLMs in navigating complex mathematical problem-solving. Through case analysis, we shed light on the gaps in LLM capabilities within mathematics, thereby setting the stage for future research and advancements in AI-driven mathematical reasoning. We make our code and findings publicly available for research: \url{https://github.com/gipplab/LLM-Investig-MathStackExchange}

Taxonomy of Mathematical Plagiarism

Plagiarism is a pressing concern, even more so with the availability of large language models. Existing plagiarism detection systems reliably find copied and moderately reworded text but fail for idea plagiarism, especially in mathematical science, which heavily uses formal mathematical notation. We make two contributions. First, we establish a taxonomy of mathematical content reuse by annotating potentially plagiarised 122 scientific document pairs. Second, we analyze the best-performing approaches to detect plagiarism and mathematical content similarity on the newly established taxonomy. We found that the best-performing methods for plagiarism and math content similarity achieve an overall detection score (PlagDet) of 0.06 and 0.16, respectively. The best-performing methods failed to detect most cases from all seven newly established math similarity types. Outlined contributions will benefit research in plagiarism detection systems, recommender systems, question-answering systems, and search engines. We make our experiment's code and annotated dataset available to the community: https://github.com/gipplab/Taxonomy-of-Mathematical-Plagiarism

Bravo MaRDI: A Wikibase Powered Knowledge Graph on Mathematics

Mathematical world knowledge is a fundamental component of Wikidata. However, to date, no expertly curated knowledge graph has focused specifically on contemporary mathematics. Addressing this gap, the Mathematical Research Data Initiative (MaRDI) has developed a comprehensive knowledge graph that links multimodal research data in mathematics. This encompasses traditional research data items like datasets, software, and publications and includes semantically advanced objects such as mathematical formulas and hypotheses. This paper details the abilities of the MaRDI knowledge graph, which is based on Wikibase, leading up to its inaugural public release, codenamed Bravo, available on https://portal.mardi4nfdi.de.

Neural Machine Translation for Mathematical Formulae

We tackle the problem of neural machine translation of mathematical formulae between ambiguous presentation languages and unambiguous content languages. Compared to neural machine translation on natural language, mathematical formulae have a much smaller vocabulary and much longer sequences of symbols, while their translation requires extreme precision to satisfy mathematical information needs. In this work, we perform the tasks of translating from LaTeX to Mathematica as well as from LaTeX to semantic LaTeX. While recurrent, recursive, and transformer networks struggle with preserving all contained information, we find that convolutional sequence-to-sequence networks achieve 95.1% and 90.7% exact matches, respectively.

TEIMMA: The First Content Reuse Annotator for Text, Images, and Math

This demo paper presents the first tool to annotate the reuse of text, images, and mathematical formulae in a document pair -- TEIMMA. Annotating content reuse is particularly useful to develop plagiarism detection algorithms. Real-world content reuse is often obfuscated, which makes it challenging to identify such cases. TEIMMA allows entering the obfuscation type to enable novel classifications for confirmed cases of plagiarism. It enables recording different reuse types for text, images, and mathematical formulae in HTML and supports users by visualizing the content reuse in a document pair using similarity detection methods for text and math.

Methods and Tools to Advance the Retrieval of Mathematical Knowledge from Digital Libraries for Search-, Recommendation-, and Assistance-Systems

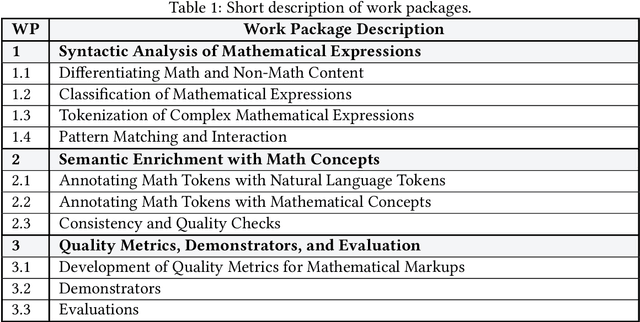
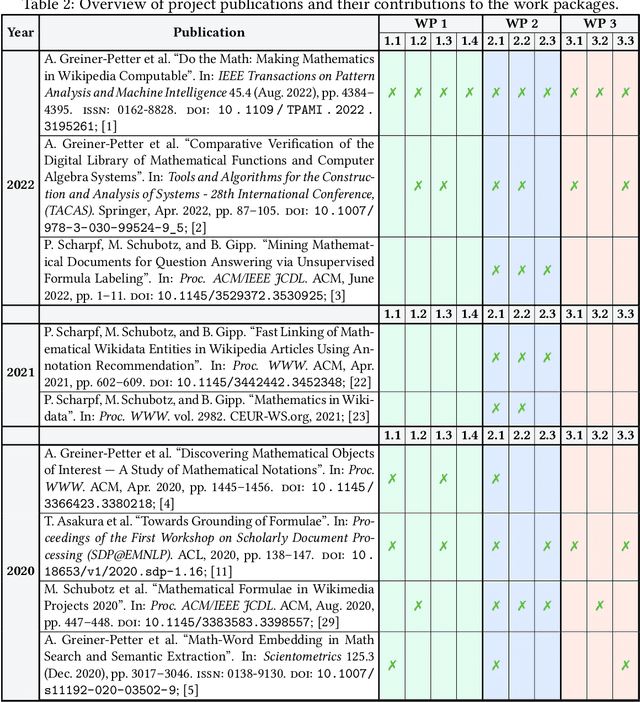
This project investigated new approaches and technologies to enhance the accessibility of mathematical content and its semantic information for a broad range of information retrieval applications. To achieve this goal, the project addressed three main research challenges: (1) syntactic analysis of mathematical expressions, (2) semantic enrichment of mathematical expressions, and (3) evaluation using quality metrics and demonstrators. To make our research useful for the research community, we published tools that enable researchers to process mathematical expressions more effectively and efficiently.

Discovery and Recognition of Formula Concepts using Machine Learning

Citation-based Information Retrieval (IR) methods for scientific documents have proven effective for IR applications, such as Plagiarism Detection or Literature Recommender Systems in academic disciplines that use many references. In science, technology, engineering, and mathematics, researchers often employ mathematical concepts through formula notation to refer to prior knowledge. Our long-term goal is to generalize citation-based IR methods and apply this generalized method to both classical references and mathematical concepts. In this paper, we suggest how mathematical formulas could be cited and define a Formula Concept Retrieval task with two subtasks: Formula Concept Discovery (FCD) and Formula Concept Recognition (FCR). While FCD aims at the definition and exploration of a 'Formula Concept' that names bundled equivalent representations of a formula, FCR is designed to match a given formula to a prior assigned unique mathematical concept identifier. We present machine learning-based approaches to address the FCD and FCR tasks. We then evaluate these approaches on a standardized test collection (NTCIR arXiv dataset). Our FCD approach yields a precision of 68% for retrieving equivalent representations of frequent formulas and a recall of 72% for extracting the formula name from the surrounding text. FCD and FCR enable the citation of formulas within mathematical documents and facilitate semantic search and question answering as well as document similarity assessments for plagiarism detection or recommender systems.

Collaborative and AI-aided Exam Question Generation using Wikidata in Education

Since the COVID-19 outbreak, the use of digital learning or education platforms has significantly increased. Teachers now digitally distribute homework and provide exercise questions. In both cases, teachers need to continuously develop novel and individual questions. This process can be very time-consuming and should be facilitated and accelerated both through exchange with other teachers and by using Artificial Intelligence (AI) capabilities. To address this need, we propose a multilingual Wikimedia framework that allows for collaborative worldwide teacher knowledge engineering and subsequent AI-aided question generation, test, and correction. As a proof of concept, we present >>PhysWikiQuiz<<, a physics question generation and test engine. Our system (hosted by Wikimedia at https://physwikiquiz.wmflabs.org) retrieves physics knowledge from the open community-curated database Wikidata. It can generate questions in different variations and verify answer values and units using a Computer Algebra System (CAS). We evaluate the performance on a public benchmark dataset at each stage of the system workflow. For an average formula with three variables, the system can generate and correct up to 300 questions for individual students based on a single formula concept name as input by the teacher.