Design Proteins Using Large Language Models: Enhancements and Comparative Analyses

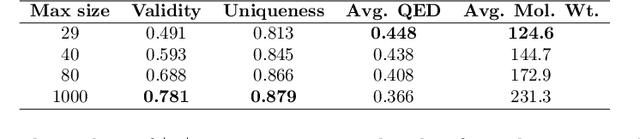
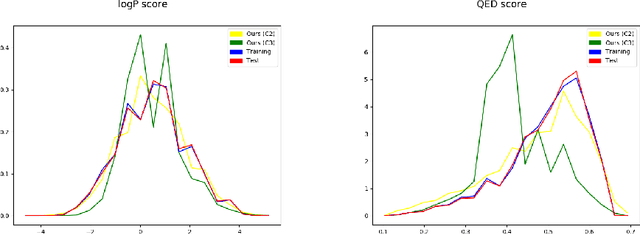
Pre-trained LLMs have demonstrated substantial capabilities across a range of conventional natural language processing (NLP) tasks, such as summarization and entity recognition. In this paper, we explore the application of LLMs in the generation of high-quality protein sequences. Specifically, we adopt a suite of pre-trained LLMs, including Mistral-7B1, Llama-2-7B2, Llama-3-8B3, and gemma-7B4, to produce valid protein sequences. All of these models are publicly available.5 Unlike previous work in this field, our approach utilizes a relatively small dataset comprising 42,000 distinct human protein sequences. We retrain these models to process protein-related data, ensuring the generation of biologically feasible protein structures. Our findings demonstrate that even with limited data, the adapted models exhibit efficiency comparable to established protein-focused models such as ProGen varieties, ProtGPT2, and ProLLaMA, which were trained on millions of protein sequences. To validate and quantify the performance of our models, we conduct comparative analyses employing standard metrics such as pLDDT, RMSD, TM-score, and REU. Furthermore, we commit to making the trained versions of all four models publicly available, fostering greater transparency and collaboration in the field of computational biology.

VC dimension of Graph Neural Networks with Pfaffian activation functions

Graph Neural Networks (GNNs) have emerged in recent years as a powerful tool to learn tasks across a wide range of graph domains in a data-driven fashion; based on a message passing mechanism, GNNs have gained increasing popularity due to their intuitive formulation, closely linked with the Weisfeiler-Lehman (WL) test for graph isomorphism, to which they have proven equivalent. From a theoretical point of view, GNNs have been shown to be universal approximators, and their generalization capability (namely, bounds on the Vapnik Chervonekis (VC) dimension) has recently been investigated for GNNs with piecewise polynomial activation functions. The aim of our work is to extend this analysis on the VC dimension of GNNs to other commonly used activation functions, such as sigmoid and hyperbolic tangent, using the framework of Pfaffian function theory. Bounds are provided with respect to architecture parameters (depth, number of neurons, input size) as well as with respect to the number of colors resulting from the 1-WL test applied on the graph domain. The theoretical analysis is supported by a preliminary experimental study.

A topological description of loss surfaces based on Betti Numbers

In the context of deep learning models, attention has recently been paid to studying the surface of the loss function in order to better understand training with methods based on gradient descent. This search for an appropriate description, both analytical and topological, has led to numerous efforts to identify spurious minima and characterize gradient dynamics. Our work aims to contribute to this field by providing a topological measure to evaluate loss complexity in the case of multilayer neural networks. We compare deep and shallow architectures with common sigmoidal activation functions by deriving upper and lower bounds on the complexity of their loss function and revealing how that complexity is influenced by the number of hidden units, training models, and the activation function used. Additionally, we found that certain variations in the loss function or model architecture, such as adding an $\ell_2$ regularization term or implementing skip connections in a feedforward network, do not affect loss topology in specific cases.

Graph Neural Networks for temporal graphs: State of the art, open challenges, and opportunities

Graph Neural Networks (GNNs) have become the leading paradigm for learning on (static) graph-structured data. However, many real-world systems are dynamic in nature, since the graph and node/edge attributes change over time. In recent years, GNN-based models for temporal graphs have emerged as a promising area of research to extend the capabilities of GNNs. In this work, we provide the first comprehensive overview of the current state-of-the-art of temporal GNN, introducing a rigorous formalization of learning settings and tasks and a novel taxonomy categorizing existing approaches in terms of how the temporal aspect is represented and processed. We conclude the survey with a discussion of the most relevant open challenges for the field, from both research and application perspectives.

A Deep Learning Approach to the Prediction of Drug Side-Effects on Molecular Graphs

Predicting drug side-effects before they occur is a key task in keeping the number of drug-related hospitalizations low and to improve drug discovery processes. Automatic predictors of side-effects generally are not able to process the structure of the drug, resulting in a loss of information. Graph neural networks have seen great success in recent years, thanks to their ability of exploiting the information conveyed by the graph structure and labels. These models have been used in a wide variety of biological applications, among which the prediction of drug side-effects on a large knowledge graph. Exploiting the molecular graph encoding the structure of the drug represents a novel approach, in which the problem is formulated as a multi-class multi-label graph-focused classification. We developed a methodology to carry out this task, using recurrent Graph Neural Networks, and building a dataset from freely accessible and well established data sources. The results show that our method has an improved classification capability, under many parameters and metrics, with respect to previously available predictors.

Modular multi-source prediction of drug side-effects with DruGNN

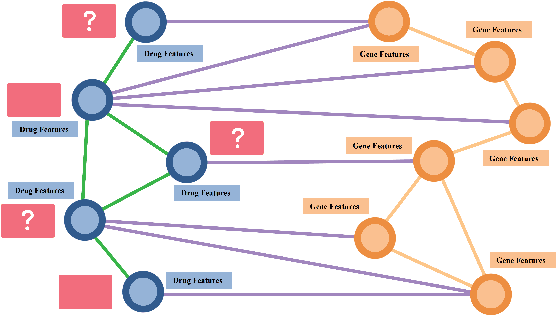
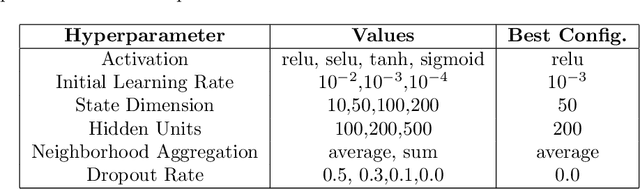
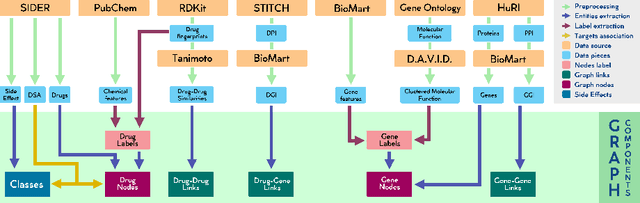
Drug Side-Effects (DSEs) have a high impact on public health, care system costs, and drug discovery processes. Predicting the probability of side-effects, before their occurrence, is fundamental to reduce this impact, in particular on drug discovery. Candidate molecules could be screened before undergoing clinical trials, reducing the costs in time, money, and health of the participants. Drug side-effects are triggered by complex biological processes involving many different entities, from drug structures to protein-protein interactions. To predict their occurrence, it is necessary to integrate data from heterogeneous sources. In this work, such heterogeneous data is integrated into a graph dataset, expressively representing the relational information between different entities, such as drug molecules and genes. The relational nature of the dataset represents an important novelty for drug side-effect predictors. Graph Neural Networks (GNNs) are exploited to predict DSEs on our dataset with very promising results. GNNs are deep learning models that can process graph-structured data, with minimal information loss, and have been applied on a wide variety of biological tasks. Our experimental results confirm the advantage of using relationships between data entities, suggesting interesting future developments in this scope. The experimentation also shows the importance of specific subsets of data in determining associations between drugs and side-effects.

A unifying point of view on expressive power of GNNs

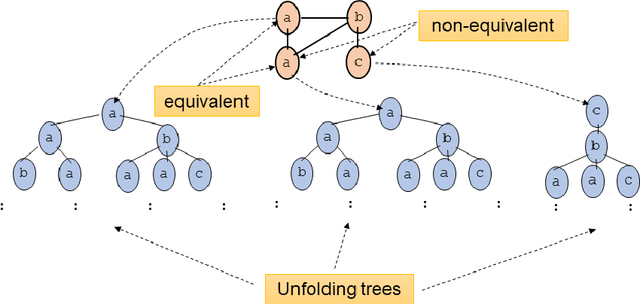
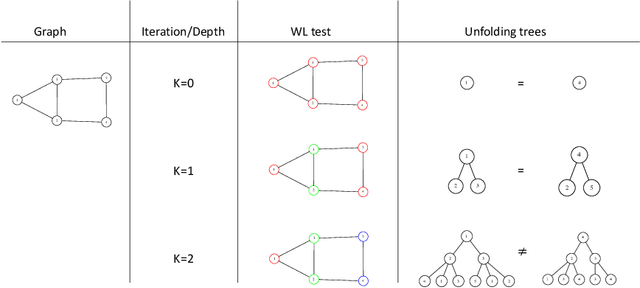
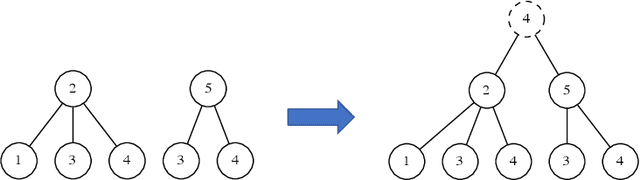
Graph Neural Networks (GNNs) are a wide class of connectionist models for graph processing. They perform an iterative message passing operation on each node and its neighbors, to solve classification/ clustering tasks -- on some nodes or on the whole graph -- collecting all such messages, regardless of their order. Despite the differences among the various models belonging to this class, most of them adopt the same computation scheme, based on a local aggregation mechanism and, intuitively, the local computation framework is mainly responsible for the expressive power of GNNs. In this paper, we prove that the Weisfeiler--Lehman test induces an equivalence relationship on the graph nodes that exactly corresponds to the unfolding equivalence, defined on the original GNN model. Therefore, the results on the expressive power of the original GNNs can be extended to general GNNs which, under mild conditions, can be proved capable of approximating, in probability and up to any precision, any function on graphs that respects the unfolding equivalence.

A multi-stage GAN for multi-organ chest X-ray image generation and segmentation

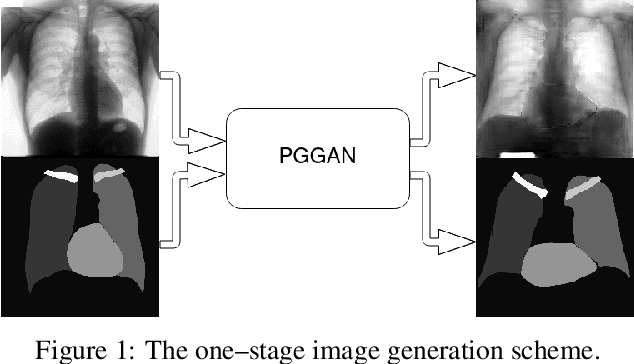
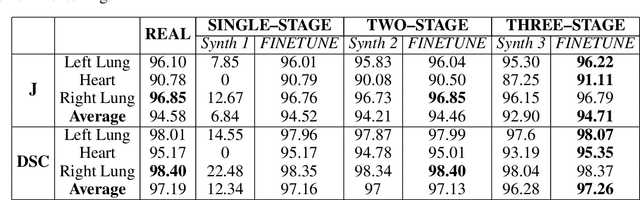
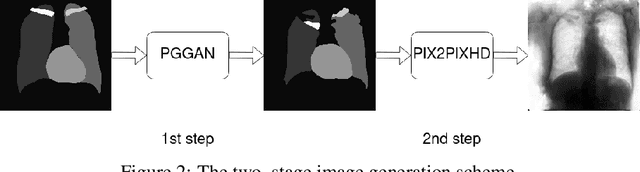
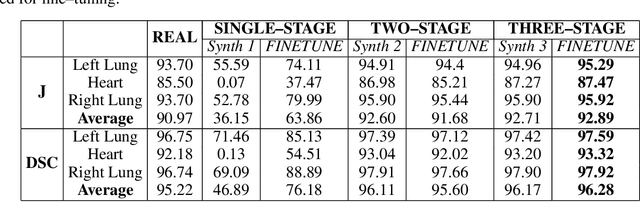
Multi-organ segmentation of X-ray images is of fundamental importance for computer aided diagnosis systems. However, the most advanced semantic segmentation methods rely on deep learning and require a huge amount of labeled images, which are rarely available due to both the high cost of human resources and the time required for labeling. In this paper, we present a novel multi-stage generation algorithm based on Generative Adversarial Networks (GANs) that can produce synthetic images along with their semantic labels and can be used for data augmentation. The main feature of the method is that, unlike other approaches, generation occurs in several stages, which simplifies the procedure and allows it to be used on very small datasets. The method has been evaluated on the segmentation of chest radiographic images, showing promising results. The multistage approach achieves state-of-the-art and, when very few images are used to train the GANs, outperforms the corresponding single-stage approach.

Molecular graph generation with Graph Neural Networks

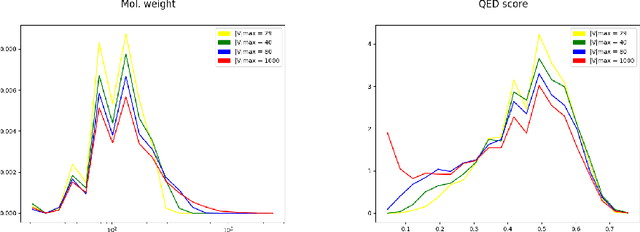
The generation of graph-structured data is an emerging problem in the field of deep learning. Various solutions have been proposed in the last few years, yet the exploration of this branch is still in an early phase. In sequential approaches, the construction of a graph is the result of a sequence of decisions, in which, at each step, a node or a group of nodes is added to the graph, along with its connections. A very relevant application of graph generation methods is the discovery of new drug molecules, which are naturally represented as graphs. In this paper, we introduce a sequential molecular graph generator based on a set of graph neural network modules, which we call MG^2N^2. Its modular architecture simplifies the training procedure, also allowing an independent retraining of a single module. The use of graph neural networks maximizes the information in input at each generative step, which consists of the subgraph produced during the previous steps. Experiments of unconditional generation on the QM9 dataset show that our model is capable of generalizing molecular patterns seen during the training phase, without overfitting. The results indicate that our method outperforms very competitive baselines, and can be placed among the state of the art approaches for unconditional generation on QM9.

Weak Supervision for Generating Pixel-Level Annotations in Scene Text Segmentation

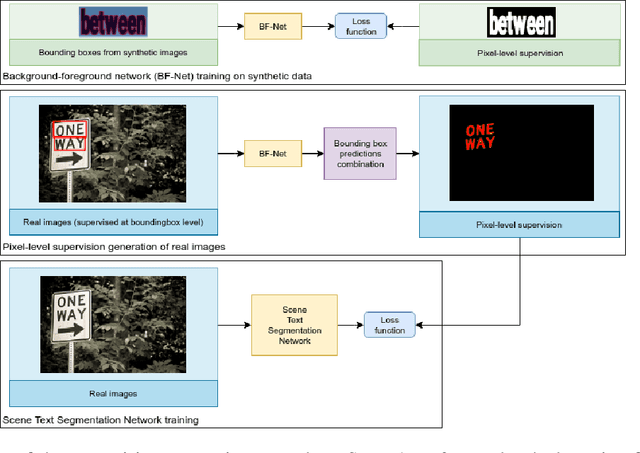
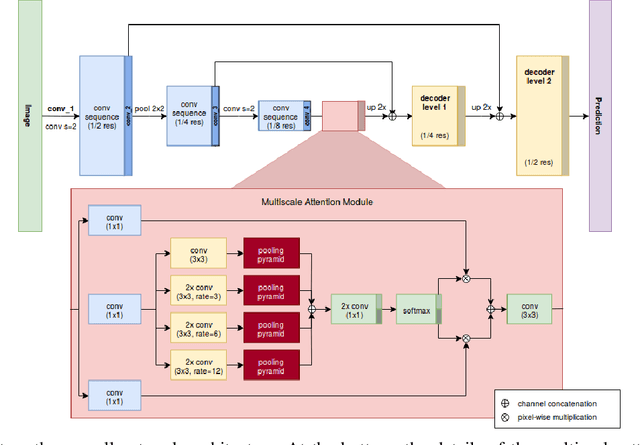
Providing pixel-level supervisions for scene text segmentation is inherently difficult and costly, so that only few small datasets are available for this task. To face the scarcity of training data, previous approaches based on Convolutional Neural Networks (CNNs) rely on the use of a synthetic dataset for pre-training. However, synthetic data cannot reproduce the complexity and variability of natural images. In this work, we propose to use a weakly supervised learning approach to reduce the domain-shift between synthetic and real data. Leveraging the bounding-box supervision of the COCO-Text and the MLT datasets, we generate weak pixel-level supervisions of real images. In particular, the COCO-Text-Segmentation (COCO_TS) and the MLT-Segmentation (MLT_S) datasets are created and released. These two datasets are used to train a CNN, the Segmentation Multiscale Attention Network (SMANet), which is specifically designed to face some peculiarities of the scene text segmentation task. The SMANet is trained end-to-end on the proposed datasets, and the experiments show that COCO_TS and MLT_S are a valid alternative to synthetic images, allowing to use only a fraction of the training samples and improving significantly the performances.