Fast yet Simple Natural-Gradient Descent for Variational Inference in Complex Models

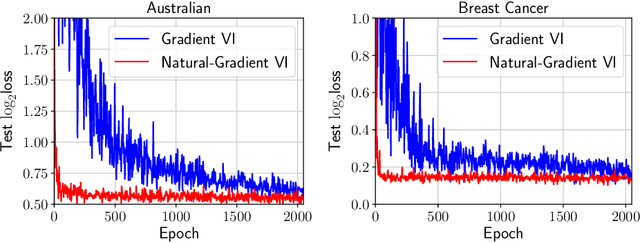
Bayesian inference plays an important role in advancing machine learning, but faces computational challenges when applied to complex models such as deep neural networks. Variational inference circumvents these challenges by formulating Bayesian inference as an optimization problem and solving it using gradient-based optimization. In this paper, we argue in favor of natural-gradient approaches which, unlike their gradient-based counterparts, can improve convergence by exploiting the information geometry of the solutions. We show how to derive fast yet simple natural-gradient updates by using a duality associated with exponential-family distributions. An attractive feature of these methods is that, by using natural-gradients, they are able to extract accurate local approximations for individual model components. We summarize recent results for Bayesian deep learning showing the superiority of natural-gradient approaches over their gradient counterparts.

Variational Message Passing with Structured Inference Networks

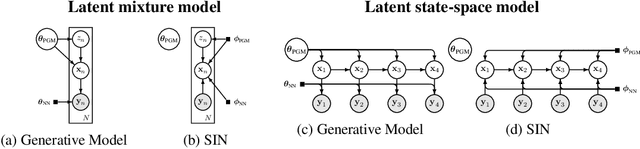
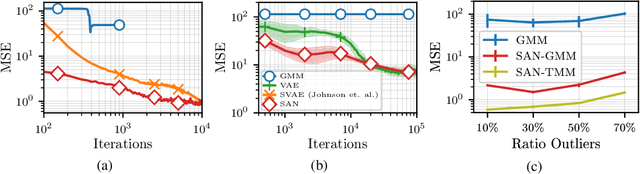
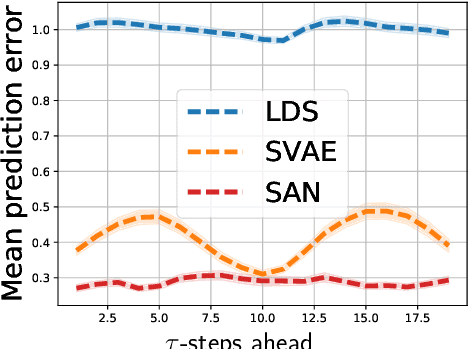
Recent efforts on combining deep models with probabilistic graphical models are promising in providing flexible models that are also easy to interpret. We propose a variational message-passing algorithm for variational inference in such models. We make three contributions. First, we propose structured inference networks that incorporate the structure of the graphical model in the inference network of variational auto-encoders (VAE). Second, we establish conditions under which such inference networks enable fast amortized inference similar to VAE. Finally, we derive a variational message passing algorithm to perform efficient natural-gradient inference while retaining the efficiency of the amortized inference. By simultaneously enabling structured, amortized, and natural-gradient inference for deep structured models, our method simplifies and generalizes existing methods.

Bayesian Nonparametric Poisson-Process Allocation for Time-Sequence Modeling

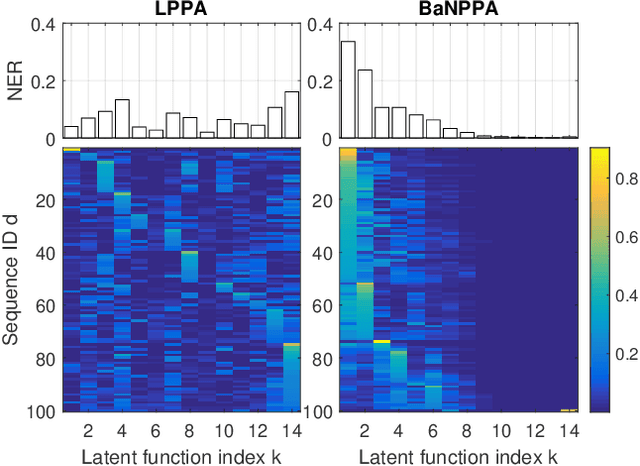
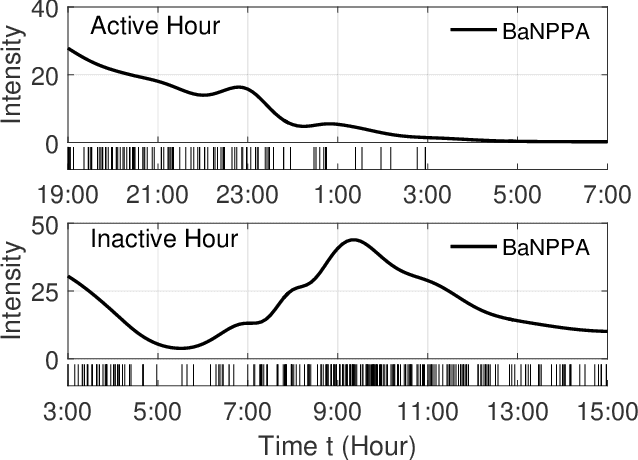
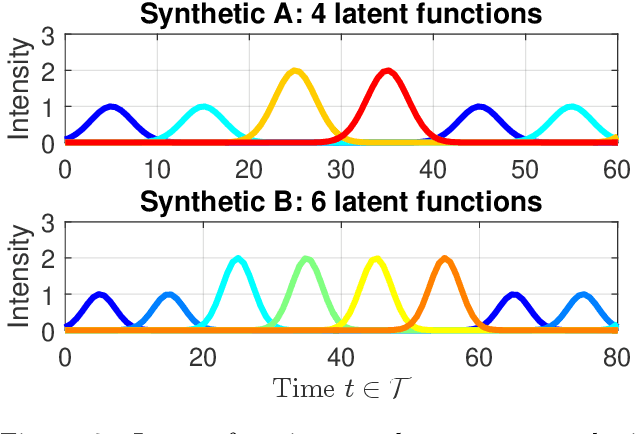
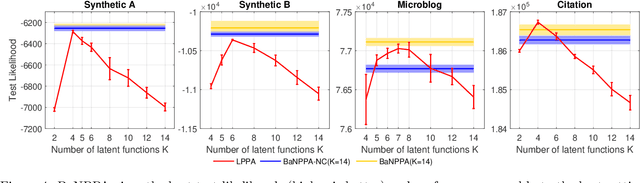
Analyzing the underlying structure of multiple time-sequences provides insights into the understanding of social networks and human activities. In this work, we present the \emph{Bayesian nonparametric Poisson process allocation} (BaNPPA), a latent-function model for time-sequences, which automatically infers the number of latent functions. We model the intensity of each sequence as an infinite mixture of latent functions, each of which is obtained using a function drawn from a Gaussian process. We show that a technical challenge for the inference of such mixture models is the unidentifiability of the weights of the latent functions. We propose to cope with the issue by regulating the volume of each latent function within a variational inference algorithm. Our algorithm is computationally efficient and scales well to large data sets. We demonstrate the usefulness of our proposed model through experiments on both synthetic and real-world data sets.

Vprop: Variational Inference using RMSprop

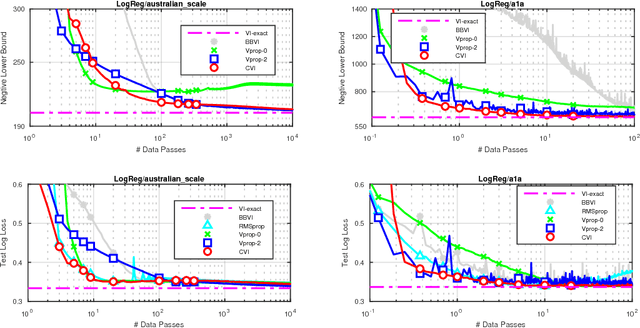
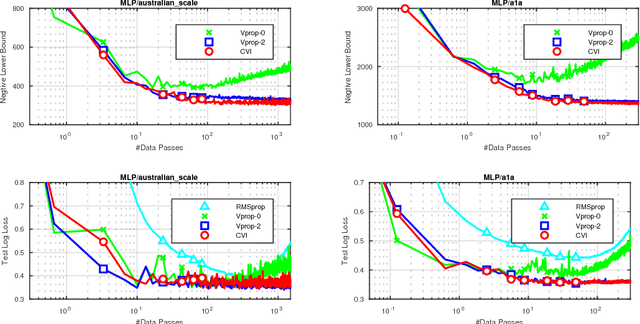
Many computationally-efficient methods for Bayesian deep learning rely on continuous optimization algorithms, but the implementation of these methods requires significant changes to existing code-bases. In this paper, we propose Vprop, a method for Gaussian variational inference that can be implemented with two minor changes to the off-the-shelf RMSprop optimizer. Vprop also reduces the memory requirements of Black-Box Variational Inference by half. We derive Vprop using the conjugate-computation variational inference method, and establish its connections to Newton's method, natural-gradient methods, and extended Kalman filters. Overall, this paper presents Vprop as a principled, computationally-efficient, and easy-to-implement method for Bayesian deep learning.

Variational Adaptive-Newton Method for Explorative Learning

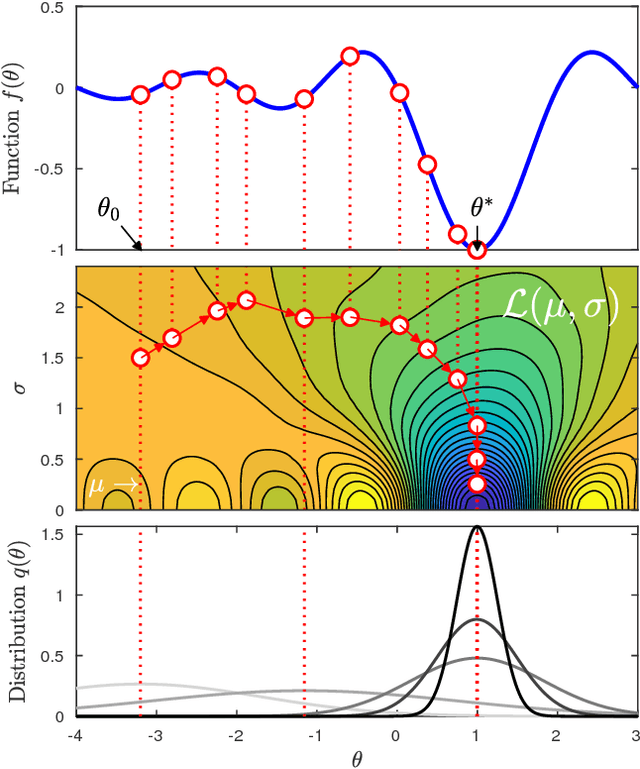
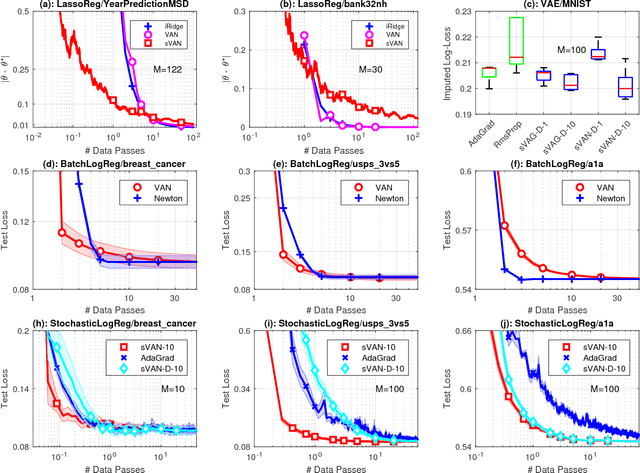
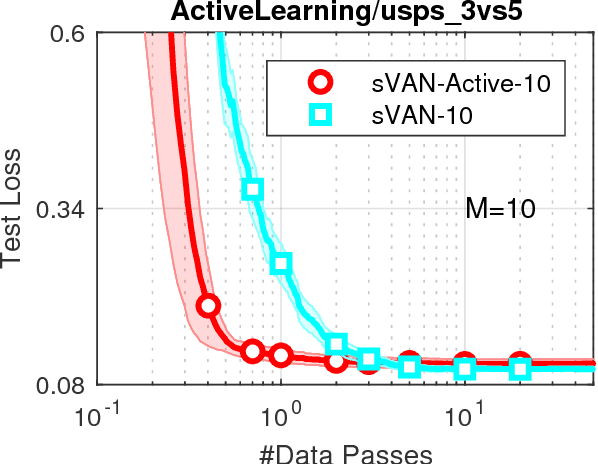
We present the Variational Adaptive Newton (VAN) method which is a black-box optimization method especially suitable for explorative-learning tasks such as active learning and reinforcement learning. Similar to Bayesian methods, VAN estimates a distribution that can be used for exploration, but requires computations that are similar to continuous optimization methods. Our theoretical contribution reveals that VAN is a second-order method that unifies existing methods in distinct fields of continuous optimization, variational inference, and evolution strategies. Our experimental results show that VAN performs well on a wide-variety of learning tasks. This work presents a general-purpose explorative-learning method that has the potential to improve learning in areas such as active learning and reinforcement learning.

Conjugate-Computation Variational Inference : Converting Variational Inference in Non-Conjugate Models to Inferences in Conjugate Models

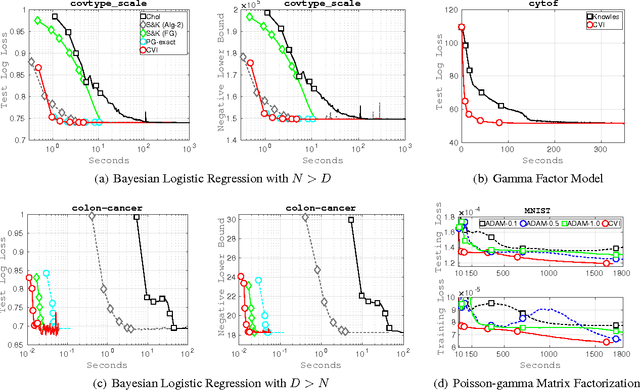
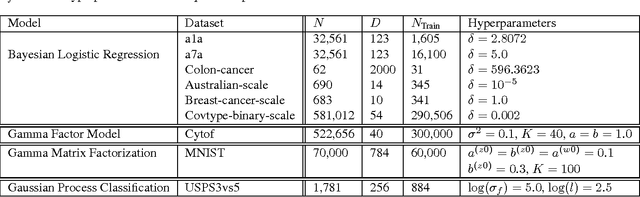
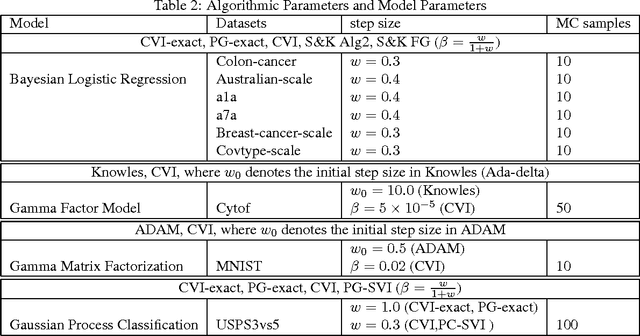
Variational inference is computationally challenging in models that contain both conjugate and non-conjugate terms. Methods specifically designed for conjugate models, even though computationally efficient, find it difficult to deal with non-conjugate terms. On the other hand, stochastic-gradient methods can handle the non-conjugate terms but they usually ignore the conjugate structure of the model which might result in slow convergence. In this paper, we propose a new algorithm called Conjugate-computation Variational Inference (CVI) which brings the best of the two worlds together -- it uses conjugate computations for the conjugate terms and employs stochastic gradients for the rest. We derive this algorithm by using a stochastic mirror-descent method in the mean-parameter space, and then expressing each gradient step as a variational inference in a conjugate model. We demonstrate our algorithm's applicability to a large class of models and establish its convergence. Our experimental results show that our method converges much faster than the methods that ignore the conjugate structure of the model.

Faster Stochastic Variational Inference using Proximal-Gradient Methods with General Divergence Functions

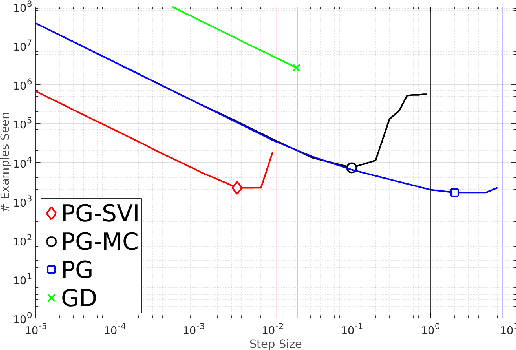
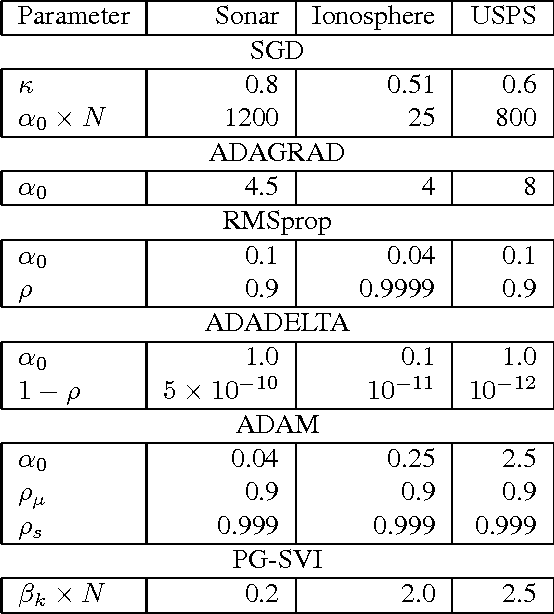
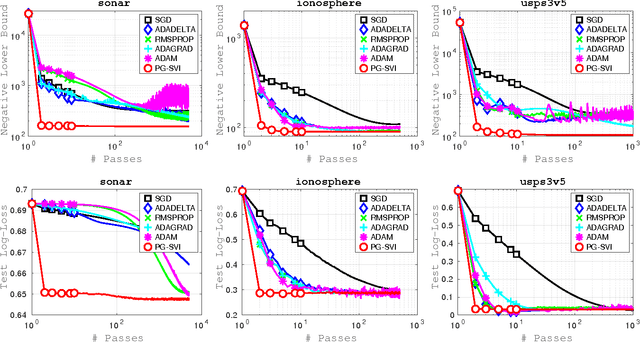
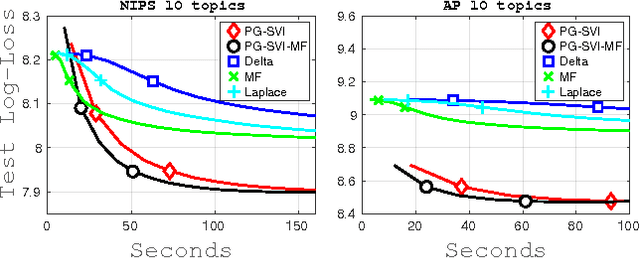
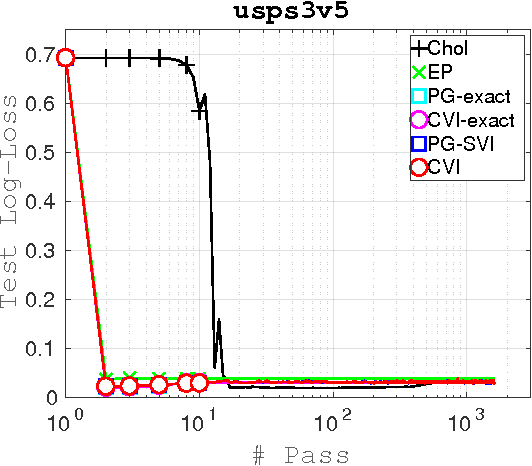
Several recent works have explored stochastic gradient methods for variational inference that exploit the geometry of the variational-parameter space. However, the theoretical properties of these methods are not well-understood and these methods typically only apply to conditionally-conjugate models. We present a new stochastic method for variational inference which exploits the geometry of the variational-parameter space and also yields simple closed-form updates even for non-conjugate models. We also give a convergence-rate analysis of our method and many other previous methods which exploit the geometry of the space. Our analysis generalizes existing convergence results for stochastic mirror-descent on non-convex objectives by using a more general class of divergence functions. Beyond giving a theoretical justification for a variety of recent methods, our experiments show that new algorithms derived in this framework lead to state of the art results on a variety of problems. Further, due to its generality, we expect that our theoretical analysis could also apply to other applications.

UAVs using Bayesian Optimization to Locate WiFi Devices

We address the problem of localizing non-collaborative WiFi devices in a large region. Our main motive is to localize humans by localizing their WiFi devices, e.g. during search-and-rescue operations after a natural disaster. We use an active sensing approach that relies on Unmanned Aerial Vehicles (UAVs) to collect signal-strength measurements at informative locations. The problem is challenging since the measurement is received at arbitrary times and they are received only when the UAV is in close proximity to the device. For these reasons, it is extremely important to make prudent decision with very few measurements. We use the Bayesian optimization approach based on Gaussian process (GP) regression. This approach works well for our application since GPs give reliable predictions with very few measurements while Bayesian optimization makes a judicious trade-off between exploration and exploitation. In field experiments conducted over a region of 1000 $\times$ 1000 $m^2$, we show that our approach reduces the search area to less than 100 meters around the WiFi device within 5 minutes only. Overall, our approach localizes the device in less than 15 minutes with an error of less than 20 meters.

Fast Dual Variational Inference for Non-Conjugate LGMs

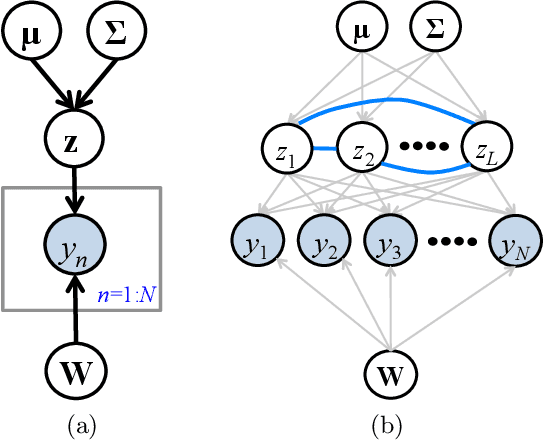
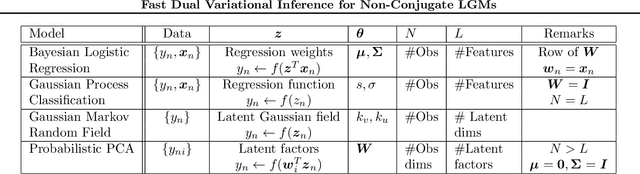
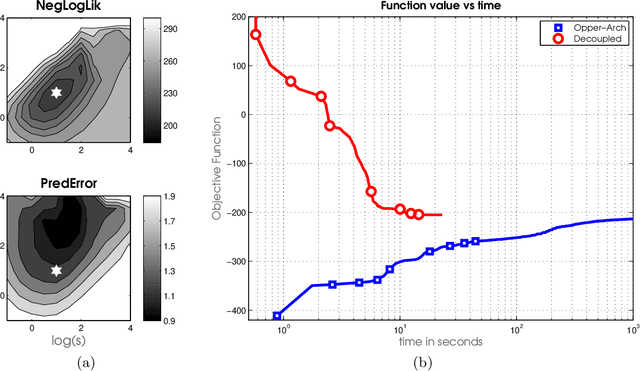
Latent Gaussian models (LGMs) are widely used in statistics and machine learning. Bayesian inference in non-conjugate LGMs is difficult due to intractable integrals involving the Gaussian prior and non-conjugate likelihoods. Algorithms based on variational Gaussian (VG) approximations are widely employed since they strike a favorable balance between accuracy, generality, speed, and ease of use. However, the structure of the optimization problems associated with these approximations remains poorly understood, and standard solvers take too long to converge. We derive a novel dual variational inference approach that exploits the convexity property of the VG approximations. We obtain an algorithm that solves a convex optimization problem, reduces the number of variational parameters, and converges much faster than previous methods. Using real-world data, we demonstrate these advantages on a variety of LGMs, including Gaussian process classification, and latent Gaussian Markov random fields.