The Bayesian Learning Rule

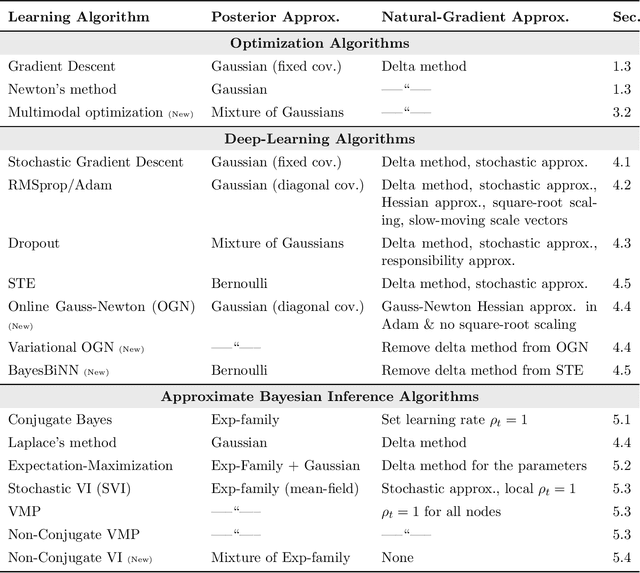
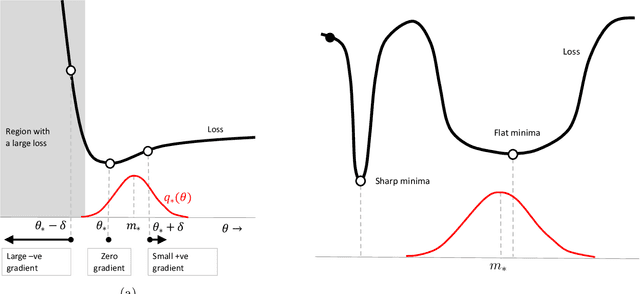
We show that many machine-learning algorithms are specific instances of a single algorithm called the Bayesian learning rule. The rule, derived from Bayesian principles, yields a wide-range of algorithms from fields such as optimization, deep learning, and graphical models. This includes classical algorithms such as ridge regression, Newton's method, and Kalman filter, as well as modern deep-learning algorithms such as stochastic-gradient descent, RMSprop, and Dropout. The key idea in deriving such algorithms is to approximate the posterior using candidate distributions estimated by using natural gradients. Different candidate distributions result in different algorithms and further approximations to natural gradients give rise to variants of those algorithms. Our work not only unifies, generalizes, and improves existing algorithms, but also helps us design new ones.

Knowledge-Adaptation Priors

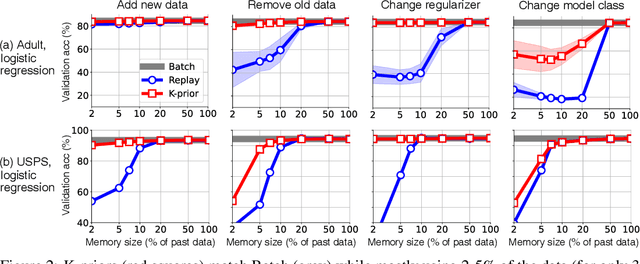
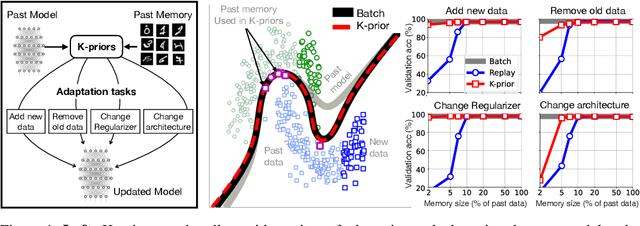
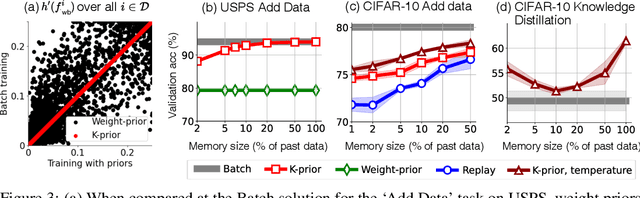
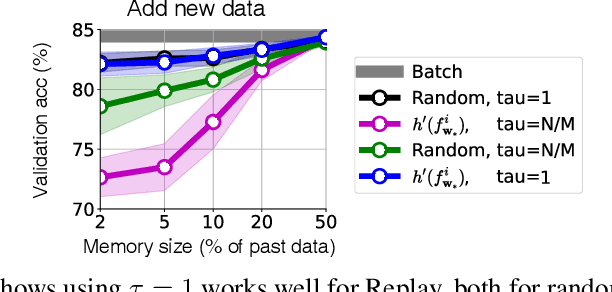
Humans and animals have a natural ability to quickly adapt to their surroundings, but machine-learning models, when subjected to changes, often require a complete retraining from scratch. We present Knowledge-adaptation priors (K-priors) to reduce the cost of retraining by enabling quick and accurate adaptation for a wide-variety of tasks and models. This is made possible by a combination of weight and function-space priors to reconstruct the gradients of the past, which recovers and generalizes many existing, but seemingly-unrelated, adaptation strategies. Training with simple first-order gradient methods can often recover the exact retrained model to an arbitrary accuracy by choosing a sufficiently large memory of the past data. Empirical results confirm that the adaptation can be cheap and accurate, and a promising alternative to retraining.

Beyond Target Networks: Improving Deep $Q$-learning with Functional Regularization

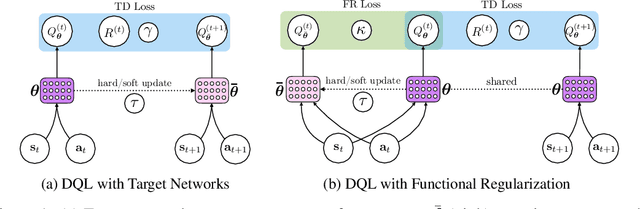
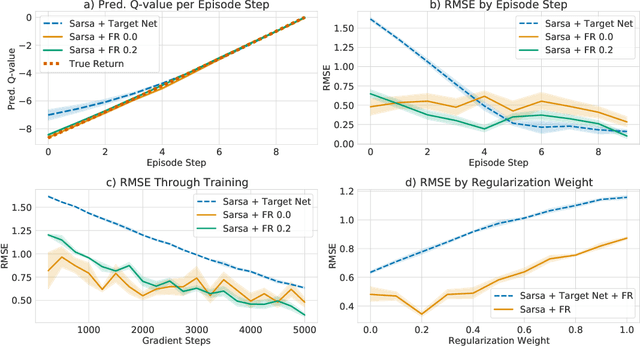
Target networks are at the core of recent success in Reinforcement Learning. They stabilize the training by using old parameters to estimate the $Q$-values, but this also limits the propagation of newly-encountered rewards which could ultimately slow down the training. In this work, we propose an alternative training method based on functional regularization which does not have this deficiency. Unlike target networks, our method uses up-to-date parameters to estimate the target $Q$-values, thereby speeding up training while maintaining stability. Surprisingly, in some cases, we can show that target networks are a special, restricted type of functional regularizers. Using this approach, we show empirical improvements in sample efficiency and performance across a range of Atari and simulated robotics environments.

Scalable Marginal Likelihood Estimation for Model Selection in Deep Learning

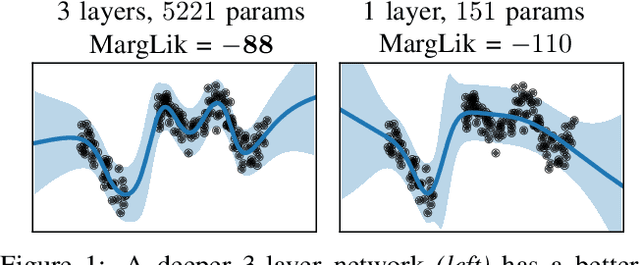
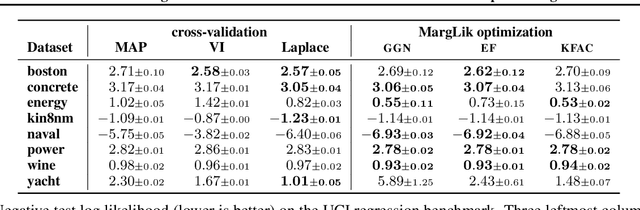
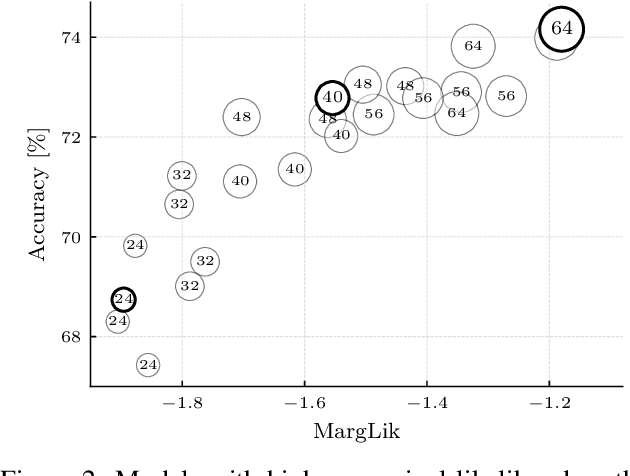
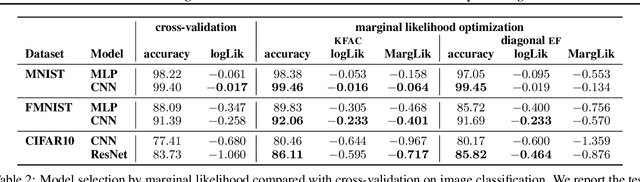
Marginal-likelihood based model-selection, even though promising, is rarely used in deep learning due to estimation difficulties. Instead, most approaches rely on validation data, which may not be readily available. In this work, we present a scalable marginal-likelihood estimation method to select both the hyperparameters and network architecture based on the training data alone. Some hyperparameters can be estimated online during training, simplifying the procedure. Our marginal-likelihood estimate is based on Laplace's method and Gauss-Newton approximations to the Hessian, and it outperforms cross-validation and manual-tuning on standard regression and image classification datasets, especially in terms of calibration and out-of-distribution detection. Our work shows that marginal likelihoods can improve generalization and be useful when validation data is unavailable (e.g., in nonstationary settings).

Tractable structured natural gradient descent using local parameterizations

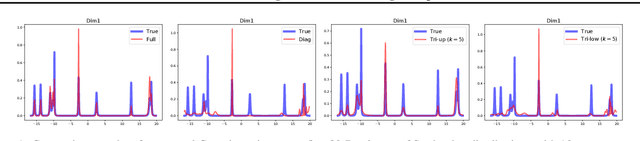
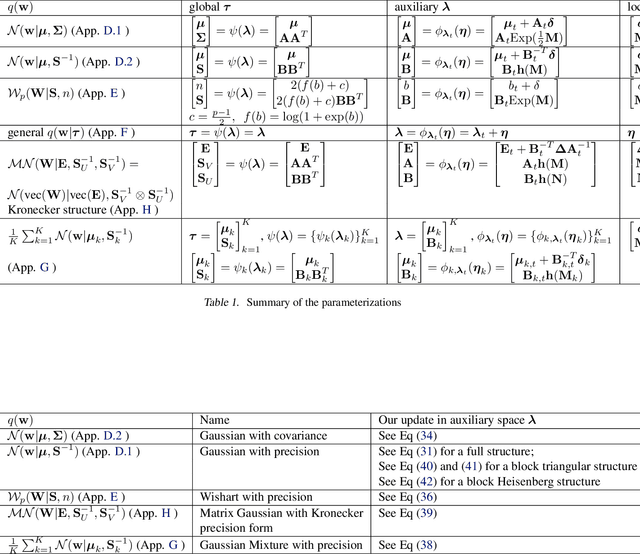
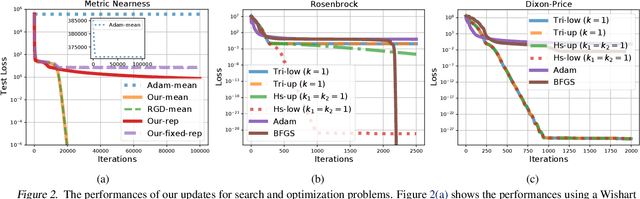
Natural-gradient descent on structured parameter spaces (e.g., low-rank covariances) is computationally challenging due to complicated inverse Fisher-matrix computations. We address this issue for optimization, inference, and search problems by using \emph{local-parameter coordinates}. Our method generalizes an existing evolutionary-strategy method, recovers Newton and Riemannian-gradient methods as special cases, and also yields new tractable natural-gradient algorithms for learning flexible covariance structures of Gaussian and Wishart-based distributions via \emph{matrix groups}. We show results on a range of applications on deep learning, variational inference, and evolution strategies. Our work opens a new direction for scalable structured geometric methods via local parameterizations.

Fast Variational Learning in State-Space Gaussian Process Models

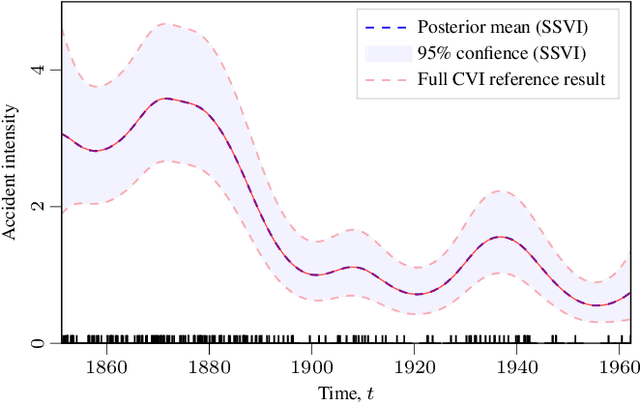
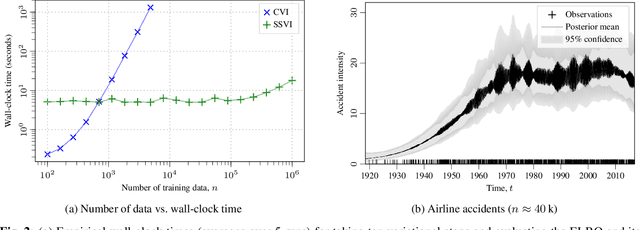
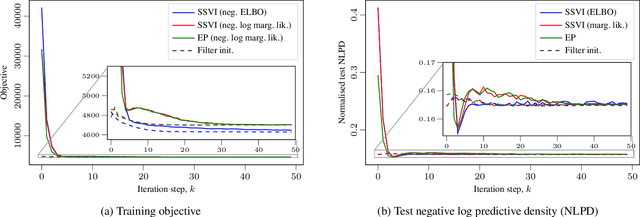
Gaussian process (GP) regression with 1D inputs can often be performed in linear time via a stochastic differential equation formulation. However, for non-Gaussian likelihoods, this requires application of approximate inference methods which can make the implementation difficult, e.g., expectation propagation can be numerically unstable and variational inference can be computationally inefficient. In this paper, we propose a new method that removes such difficulties. Building upon an existing method called conjugate-computation variational inference, our approach enables linear-time inference via Kalman recursions while avoiding numerical instabilities and convergence issues. We provide an efficient JAX implementation which exploits just-in-time compilation and allows for fast automatic differentiation through large for-loops. Overall, our approach leads to fast and stable variational inference in state-space GP models that can be scaled to time series with millions of data points.

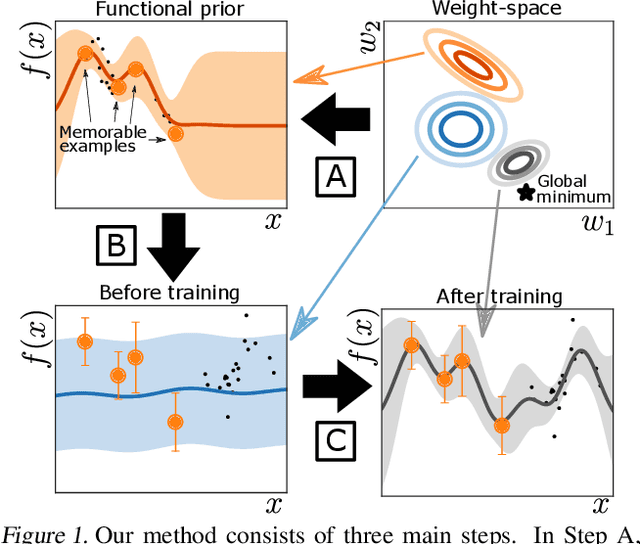
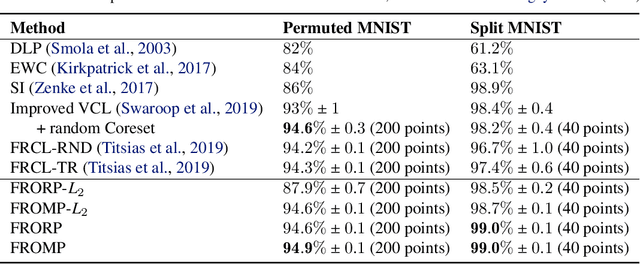
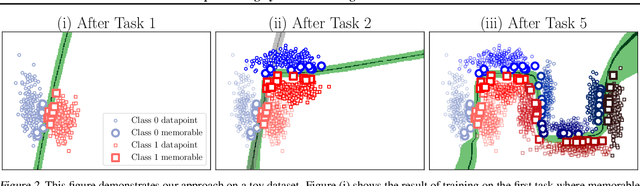
Continual Deep Learning by Functional Regularisation of Memorable Past

Continually learning new skills is important for intelligent systems, yet most deep learning methods suffer from catastrophic forgetting of the past. Recent works address this with weight regularisation. Functional regularisation, although computationally expensive, is expected to perform better, but rarely does so in practice. In this paper, we fix this issue by proposing a new functional-regularisation approach that utilises a few memorable past examples that are crucial to avoid forgetting. By using a Gaussian Process formulation of deep networks, our approach enables training in weight-space while identifying both the memorable past and a functional prior. Our method achieves state-of-the-art performance on standard benchmarks and opens a new direction for life-long learning where regularisation and memory-based methods are naturally combined.

Training Binary Neural Networks using the Bayesian Learning Rule

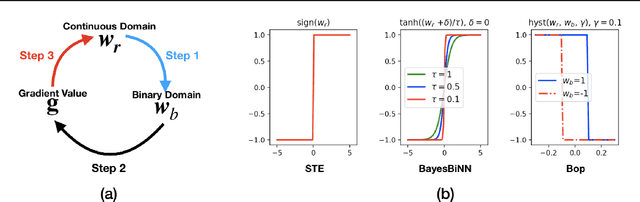
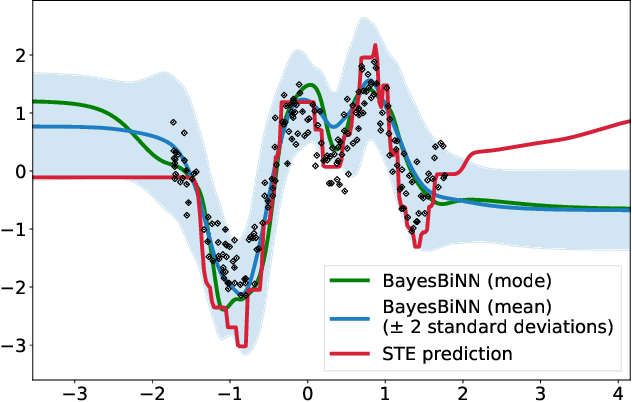
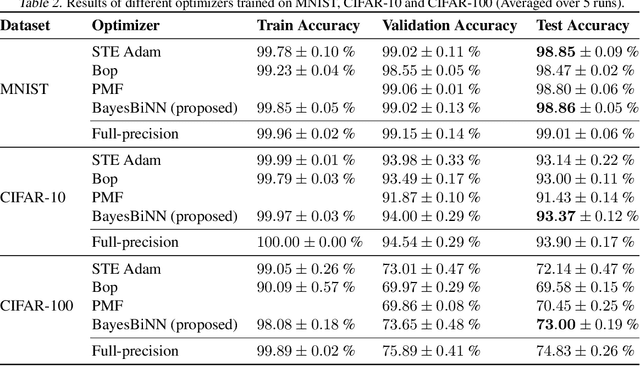
Neural networks with binary weights are computation-efficient and hardware-friendly, but their training is challenging because it involves a discrete optimization problem. Surprisingly, ignoring the discrete nature of the problem and using gradient-based methods, such as Straight-Through Estimator, still works well in practice. This raises the question: are there principled approaches which justify such methods? In this paper, we propose such an approach using the Bayesian learning rule. The rule, when applied to estimate a Bernoulli distribution over the binary weights, results in an algorithm which justifies some of the algorithmic choices made by the previous approaches. The algorithm not only obtains state-of-the-art performance, but also enables uncertainty estimation for continual learning to avoid catastrophic forgetting. Our work provides a principled approach for training binary neural networks which justifies and extends existing approaches.

Handling the Positive-Definite Constraint in the Bayesian Learning Rule

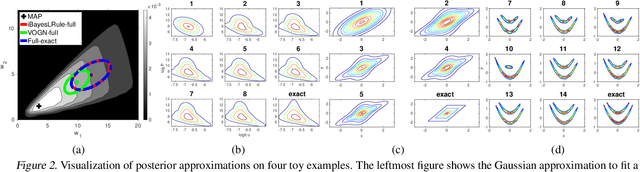
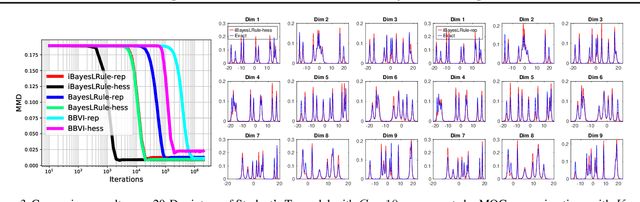
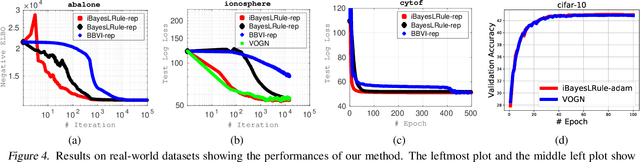
The Bayesian learning rule is a recently proposed variational inference method, which not only contains many existing learning algorithms as special cases but also enables the design of new algorithms. Unfortunately, when posterior parameters lie in an open constraint set, the rule may not satisfy the constraints and requires line-searches which could slow down the algorithm. In this paper, we fix this issue for the positive-definite constraint by proposing an improved rule that naturally handles the constraint. Our modification is obtained using Riemannian gradient methods, and is valid when the approximation attains a \emph{block-coordinate natural parameterization} (e.g., Gaussian distributions and their mixtures). Our method outperforms existing methods without any significant increase in computation. Our work makes it easier to apply the learning rule in the presence of positive-definite constraints in parameter spaces.

Stein's Lemma for the Reparameterization Trick with Exponential Family Mixtures

Stein's method (Stein, 1973; 1981) is a powerful tool for statistical applications, and has had a significant impact in machine learning. Stein's lemma plays an essential role in Stein's method. Previous applications of Stein's lemma either required strong technical assumptions or were limited to Gaussian distributions with restricted covariance structures. In this work, we extend Stein's lemma to exponential-family mixture distributions including Gaussian distributions with full covariance structures. Our generalization enables us to establish a connection between Stein's lemma and the reparamterization trick to derive gradients of expectations of a large class of functions under weak assumptions. Using this connection, we can derive many new reparameterizable gradient-identities that goes beyond the reach of existing works. For example, we give gradient identities when expectation is taken with respect to Student's t-distribution, skew Gaussian, exponentially modified Gaussian, and normal inverse Gaussian.