Efficient Autoregressive Inference for Transformer Probabilistic Models

Transformer-based models for amortized probabilistic inference, such as neural processes, prior-fitted networks, and tabular foundation models, excel at single-pass marginal prediction. However, many real-world applications, from signal interpolation to multi-column tabular predictions, require coherent joint distributions that capture dependencies between predictions. While purely autoregressive architectures efficiently generate such distributions, they sacrifice the flexible set-conditioning that makes these models powerful for meta-learning. Conversely, the standard approach to obtain joint distributions from set-based models requires expensive re-encoding of the entire augmented conditioning set at each autoregressive step. We introduce a causal autoregressive buffer that preserves the advantages of both paradigms. Our approach decouples context encoding from updating the conditioning set. The model processes the context once and caches it. A dynamic buffer then captures target dependencies: as targets are incorporated, they enter the buffer and attend to both the cached context and previously buffered targets. This enables efficient batched autoregressive generation and one-pass joint log-likelihood evaluation. A unified training strategy allows seamless integration of set-based and autoregressive modes at minimal additional cost. Across synthetic functions, EEG signals, cognitive models, and tabular data, our method matches predictive accuracy of strong baselines while delivering up to 20 times faster joint sampling. Our approach combines the efficiency of autoregressive generative models with the representational power of set-based conditioning, making joint prediction practical for transformer-based probabilistic models.

Amortized Probabilistic Conditioning for Optimization, Simulation and Inference

Amortized meta-learning methods based on pre-training have propelled fields like natural language processing and vision. Transformer-based neural processes and their variants are leading models for probabilistic meta-learning with a tractable objective. Often trained on synthetic data, these models implicitly capture essential latent information in the data-generation process. However, existing methods do not allow users to flexibly inject (condition on) and extract (predict) this probabilistic latent information at runtime, which is key to many tasks. We introduce the Amortized Conditioning Engine (ACE), a new transformer-based meta-learning model that explicitly represents latent variables of interest. ACE affords conditioning on both observed data and interpretable latent variables, the inclusion of priors at runtime, and outputs predictive distributions for discrete and continuous data and latents. We show ACE's modeling flexibility and performance in diverse tasks such as image completion and classification, Bayesian optimization, and simulation-based inference.

Memory-Based Dual Gaussian Processes for Sequential Learning

Sequential learning with Gaussian processes (GPs) is challenging when access to past data is limited, for example, in continual and active learning. In such cases, errors can accumulate over time due to inaccuracies in the posterior, hyperparameters, and inducing points, making accurate learning challenging. Here, we present a method to keep all such errors in check using the recently proposed dual sparse variational GP. Our method enables accurate inference for generic likelihoods and improves learning by actively building and updating a memory of past data. We demonstrate its effectiveness in several applications involving Bayesian optimization, active learning, and continual learning.

Fantasizing with Dual GPs in Bayesian Optimization and Active Learning

Gaussian processes (GPs) are the main surrogate functions used for sequential modelling such as Bayesian Optimization and Active Learning. Their drawbacks are poor scaling with data and the need to run an optimization loop when using a non-Gaussian likelihood. In this paper, we focus on `fantasizing' batch acquisition functions that need the ability to condition on new fantasized data computationally efficiently. By using a sparse Dual GP parameterization, we gain linear scaling with batch size as well as one-step updates for non-Gaussian likelihoods, thus extending sparse models to greedy batch fantasizing acquisition functions.

Dual Parameterization of Sparse Variational Gaussian Processes

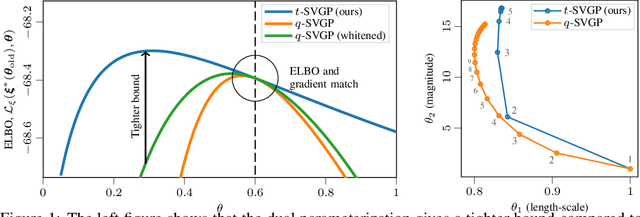
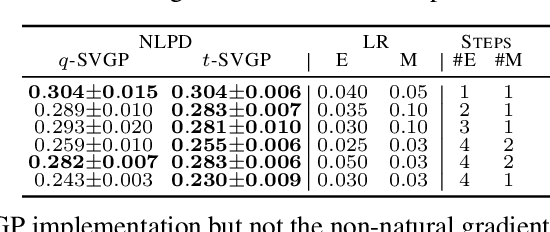
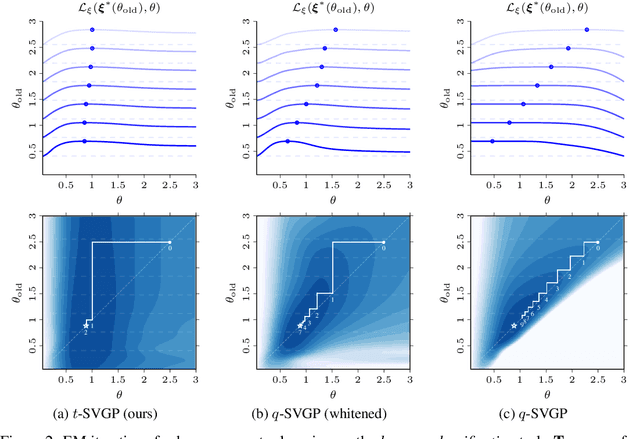
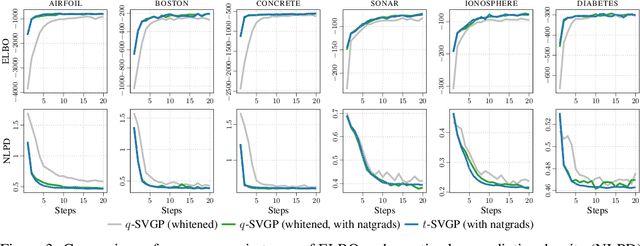
Sparse variational Gaussian process (SVGP) methods are a common choice for non-conjugate Gaussian process inference because of their computational benefits. In this paper, we improve their computational efficiency by using a dual parameterization where each data example is assigned dual parameters, similarly to site parameters used in expectation propagation. Our dual parameterization speeds-up inference using natural gradient descent, and provides a tighter evidence lower bound for hyperparameter learning. The approach has the same memory cost as the current SVGP methods, but it is faster and more accurate.

Fast Variational Learning in State-Space Gaussian Process Models

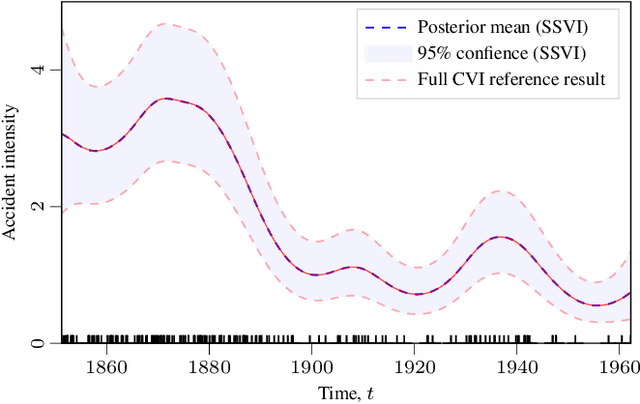
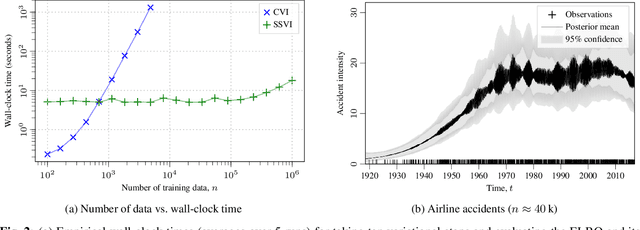
Gaussian process (GP) regression with 1D inputs can often be performed in linear time via a stochastic differential equation formulation. However, for non-Gaussian likelihoods, this requires application of approximate inference methods which can make the implementation difficult, e.g., expectation propagation can be numerically unstable and variational inference can be computationally inefficient. In this paper, we propose a new method that removes such difficulties. Building upon an existing method called conjugate-computation variational inference, our approach enables linear-time inference via Kalman recursions while avoiding numerical instabilities and convergence issues. We provide an efficient JAX implementation which exploits just-in-time compilation and allows for fast automatic differentiation through large for-loops. Overall, our approach leads to fast and stable variational inference in state-space GP models that can be scaled to time series with millions of data points.

State Space Expectation Propagation: Efficient Inference Schemes for Temporal Gaussian Processes

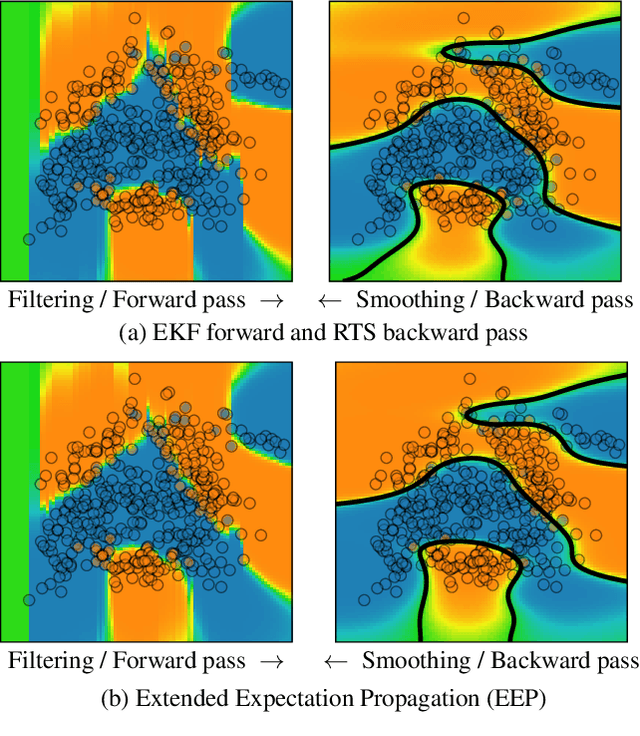
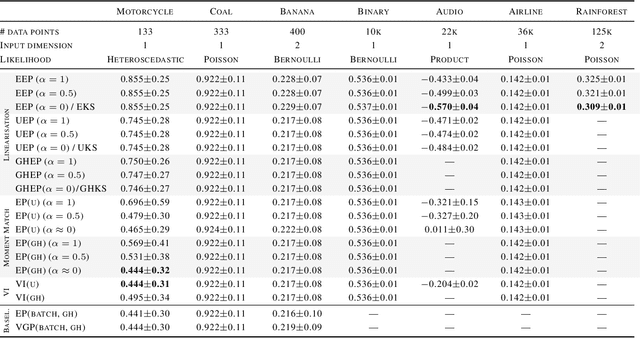
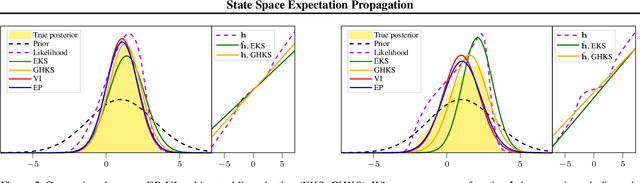
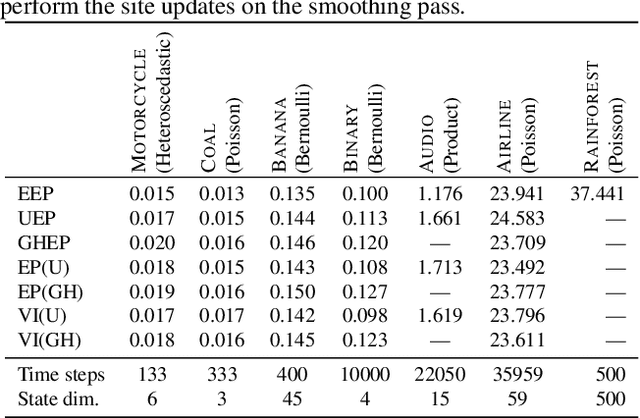
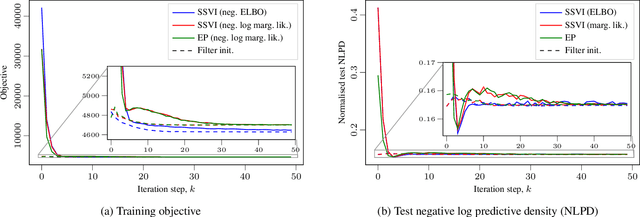
We formulate approximate Bayesian inference in non-conjugate temporal and spatio-temporal Gaussian process models as a simple parameter update rule applied during Kalman smoothing. This viewpoint encompasses most inference schemes, including expectation propagation (EP), the classical (Extended, Unscented, etc.) Kalman smoothers, and variational inference. We provide a unifying perspective on these algorithms, showing how replacing the power EP moment matching step with linearisation recovers the classical smoothers. EP provides some benefits over the traditional methods via introduction of the so-called cavity distribution, and we combine these benefits with the computational efficiency of linearisation, providing extensive empirical analysis demonstrating the efficacy of various algorithms under this unifying framework. We provide a fast implementation of all methods in JAX.