Game of Coding: Coding Theory in the Presence of Rational Adversaries, Motivated by Decentralized Machine Learning

Coding theory plays a crucial role in enabling reliable communication, storage, and computation. Classical approaches assume a worst-case adversarial model and ensure error correction and data recovery only when the number of honest nodes exceeds the number of adversarial ones by some margin. However, in some emerging decentralized applications, particularly in decentralized machine learning (DeML), participating nodes are rewarded for accepted contributions. This incentive structure naturally gives rise to rational adversaries who act strategically rather than behaving in purely malicious ways. In this paper, we first motivate the need for coding in the presence of rational adversaries, particularly in the context of outsourced computation in decentralized systems. We contrast this need with existing approaches and highlight their limitations. We then introduce the game of coding, a novel game-theoretic framework that extends coding theory to trust-minimized settings where honest nodes are not in the majority. Focusing on repetition coding, we highlight two key features of this framework: (1) the ability to achieve a non-zero probability of data recovery even when adversarial nodes are in the majority, and (2) Sybil resistance, i.e., the equilibrium remains unchanged even as the number of adversarial nodes increases. Finally, we explore scenarios in which the adversary's strategy is unknown and outline several open problems for future research.

Adversarial Robustness of Nonparametric Regression

In this paper, we investigate the adversarial robustness of regression, a fundamental problem in machine learning, under the setting where an adversary can arbitrarily corrupt a subset of the input data. While the robustness of parametric regression has been extensively studied, its nonparametric counterpart remains largely unexplored. We characterize the adversarial robustness in nonparametric regression, assuming the regression function belongs to the second-order Sobolev space (i.e., it is square integrable up to its second derivative). The contribution of this paper is two-fold: (i) we establish a minimax lower bound on the estimation error, revealing a fundamental limit that no estimator can overcome, and (ii) we show that, perhaps surprisingly, the classical smoothing spline estimator, when properly regularized, exhibits robustness against adversarial corruption. These results imply that if $o(n)$ out of $n$ samples are corrupted, the estimation error of the smoothing spline vanishes as $n \to \infty$. On the other hand, when a constant fraction of the data is corrupted, no estimator can guarantee vanishing estimation error, implying the optimality of the smoothing spline in terms of maximum tolerable number of corrupted samples.

\texttt{Range-Arithmetic}: Verifiable Deep Learning Inference on an Untrusted Party

Verifiable computing (VC) has gained prominence in decentralized machine learning systems, where resource-intensive tasks like deep neural network (DNN) inference are offloaded to external participants due to blockchain limitations. This creates a need to verify the correctness of outsourced computations without re-execution. We propose \texttt{Range-Arithmetic}, a novel framework for efficient and verifiable DNN inference that transforms non-arithmetic operations, such as rounding after fixed-point matrix multiplication and ReLU, into arithmetic steps verifiable using sum-check protocols and concatenated range proofs. Our approach avoids the complexity of Boolean encoding, high-degree polynomials, and large lookup tables while remaining compatible with finite-field-based proof systems. Experimental results show that our method not only matches the performance of existing approaches, but also reduces the computational cost of verifying the results, the computational effort required from the untrusted party performing the DNN inference, and the communication overhead between the two sides.

General Coded Computing: Adversarial Settings

Conventional coded computing frameworks are predominantly tailored for structured computations, such as matrix multiplication and polynomial evaluation. Such tasks allow the reuse of tools and techniques from algebraic coding theory to improve the reliability of distributed systems in the presence of stragglers and adversarial servers. This paper lays the foundation for general coded computing, which extends the applicability of coded computing to handle a wide class of computations. In addition, it particularly addresses the challenging problem of managing adversarial servers. We demonstrate that, in the proposed scheme, for a system with $N$ servers, where $\mathcal{O}(N^a)$, $a \in [0,1)$, are adversarial, the supremum of the average approximation error over all adversarial strategies decays at a rate of $N^{\frac{6}{5}(a-1)}$, under minimal assumptions on the computing tasks. Furthermore, we show that within a general framework, the proposed scheme achieves optimal adversarial robustness, in terms of maximum number of adversarial servers it can tolerate. This marks a significant step toward practical and reliable general coded computing. Implementation results further validate the effectiveness of the proposed method in handling various computations, including inference in deep neural networks.

Game of Coding With an Unknown Adversary

Motivated by emerging decentralized applications, the \emph{game of coding} framework has been recently introduced to address scenarios where the adversary's control over coded symbols surpasses the fundamental limits of traditional coding theory. Still, the reward mechanism available in decentralized systems, motivates the adversary to act rationally. While the decoder, as the data collector (DC), has an acceptance and rejection mechanism, followed by an estimation module, the adversary aims to maximize its utility, as an increasing function of (1) the chance of acceptance (to increase the reward), and (2) estimation error. On the other hand, the decoder also adjusts its acceptance rule to maximize its own utility, as (1) an increasing function of the chance of acceptance (to keep the system functional), (2) decreasing function of the estimation error. Prior works within this framework rely on the assumption that the game is complete, that is, both the DC and the adversary are fully aware of each other's utility functions. However, in practice, the decoder is often unaware of the utility of the adversary. To address this limitation, we develop an algorithm enabling the DC to commit to a strategy that achieves within the vicinity of the equilibrium, without knowledge of the adversary's utility function. Our approach builds on an observation that at the equilibrium, the relationship between the probability of acceptance and the mean squared error (MSE) follows a predetermined curve independent of the specific utility functions of the players. By exploiting this invariant relationship, the DC can iteratively refine its strategy based on observable parameters, converging to a near-optimal solution. We provide theoretical guarantees on sample complexity and accuracy of the proposed scheme.

Private, Augmentation-Robust and Task-Agnostic Data Valuation Approach for Data Marketplace

Evaluating datasets in data marketplaces, where the buyer aim to purchase valuable data, is a critical challenge. In this paper, we introduce an innovative task-agnostic data valuation method called PriArTa which is an approach for computing the distance between the distribution of the buyer's existing dataset and the seller's dataset, allowing the buyer to determine how effectively the new data can enhance its dataset. PriArTa is communication-efficient, enabling the buyer to evaluate datasets without needing access to the entire dataset from each seller. Instead, the buyer requests that sellers perform specific preprocessing on their data and then send back the results. Using this information and a scoring metric, the buyer can evaluate the dataset. The preprocessing is designed to allow the buyer to compute the score while preserving the privacy of each seller's dataset, mitigating the risk of information leakage before the purchase. A key feature of PriArTa is its robustness to common data transformations, ensuring consistent value assessment and reducing the risk of purchasing redundant data. The effectiveness of PriArTa is demonstrated through experiments on real-world image datasets, showing its ability to perform privacy-preserving, augmentation-robust data valuation in data marketplaces.

Coded Computing: A Learning-Theoretic Framework

Coded computing has emerged as a promising framework for tackling significant challenges in large-scale distributed computing, including the presence of slow, faulty, or compromised servers. In this approach, each worker node processes a combination of the data, rather than the raw data itself. The final result then is decoded from the collective outputs of the worker nodes. However, there is a significant gap between current coded computing approaches and the broader landscape of general distributed computing, particularly when it comes to machine learning workloads. To bridge this gap, we propose a novel foundation for coded computing, integrating the principles of learning theory, and developing a new framework that seamlessly adapts with machine learning applications. In this framework, the objective is to find the encoder and decoder functions that minimize the loss function, defined as the mean squared error between the estimated and true values. Facilitating the search for the optimum decoding and functions, we show that the loss function can be upper-bounded by the summation of two terms: the generalization error of the decoding function and the training error of the encoding function. Focusing on the second-order Sobolev space, we then derive the optimal encoder and decoder. We show that in the proposed solution, the mean squared error of the estimation decays with the rate of $O(S^4 N^{-3})$ and $O(S^{\frac{8}{5}}N^{\frac{-3}{5}})$ in noiseless and noisy computation settings, respectively, where $N$ is the number of worker nodes with at most $S$ slow servers (stragglers). Finally, we evaluate the proposed scheme on inference tasks for various machine learning models and demonstrate that the proposed framework outperforms the state-of-the-art in terms of accuracy and rate of convergence.

NeRCC: Nested-Regression Coded Computing for Resilient Distributed Prediction Serving Systems

Resilience against stragglers is a critical element of prediction serving systems, tasked with executing inferences on input data for a pre-trained machine-learning model. In this paper, we propose NeRCC, as a general straggler-resistant framework for approximate coded computing. NeRCC includes three layers: (1) encoding regression and sampling, which generates coded data points, as a combination of original data points, (2) computing, in which a cluster of workers run inference on the coded data points, (3) decoding regression and sampling, which approximately recovers the predictions of the original data points from the available predictions on the coded data points. We argue that the overall objective of the framework reveals an underlying interconnection between two regression models in the encoding and decoding layers. We propose a solution to the nested regressions problem by summarizing their dependence on two regularization terms that are jointly optimized. Our extensive experiments on different datasets and various machine learning models, including LeNet5, RepVGG, and Vision Transformer (ViT), demonstrate that NeRCC accurately approximates the original predictions in a wide range of stragglers, outperforming the state-of-the-art by up to 23%.

Byzantine-Resistant Secure Aggregation for Federated Learning Based on Coded Computing and Vector Commitment

In this paper, we propose an efficient secure aggregation scheme for federated learning that is protected against Byzantine attacks and privacy leakages. Processing individual updates to manage adversarial behavior, while preserving privacy of data against colluding nodes, requires some sort of secure secret sharing. However, communication load for secret sharing of long vectors of updates can be very high. To resolve this issue, in the proposed scheme, local updates are partitioned into smaller sub-vectors and shared using ramp secret sharing. However, this sharing method does not admit bi-linear computations, such as pairwise distance calculations, needed by outlier-detection algorithms. To overcome this issue, each user runs another round of ramp sharing, with different embedding of data in the sharing polynomial. This technique, motivated by ideas from coded computing, enables secure computation of pairwise distance. In addition, to maintain the integrity and privacy of the local update, the proposed scheme also uses a vector commitment method, in which the commitment size remains constant (i.e. does not increase with the length of the local update), while simultaneously allowing verification of the secret sharing process.

SwiftAgg+: Achieving Asymptotically Optimal Communication Load in Secure Aggregation for Federated Learning

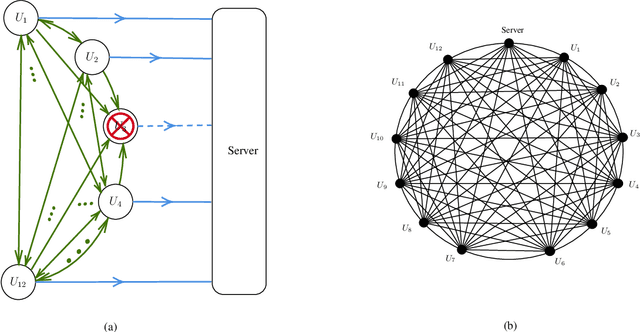
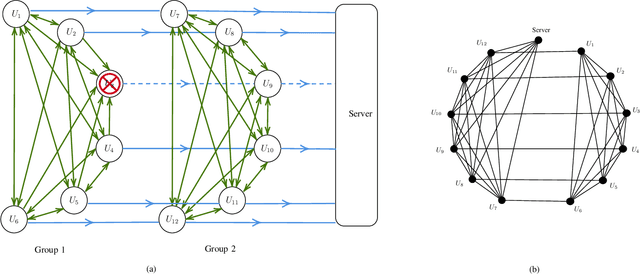
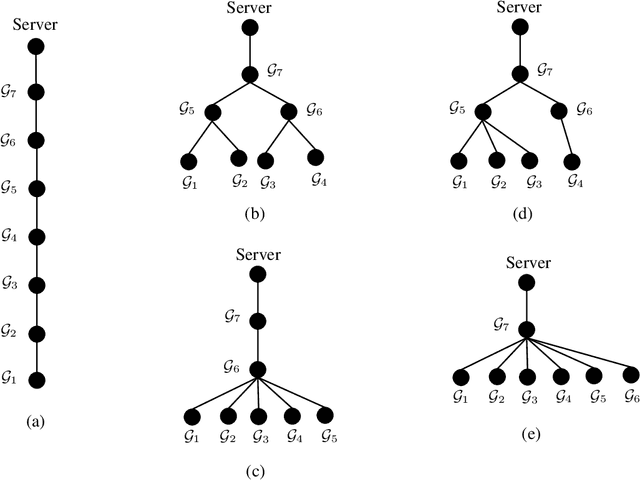
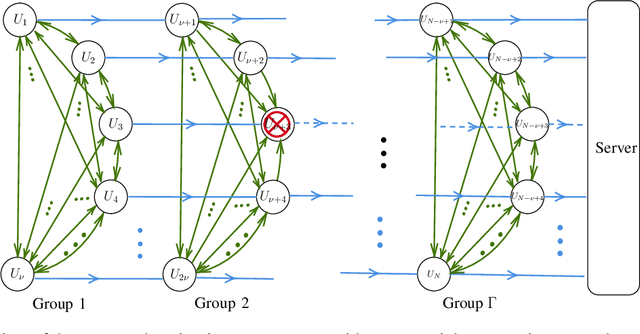
We propose SwiftAgg+, a novel secure aggregation protocol for federated learning systems, where a central server aggregates local models of $N\in\mathbb{N}$ distributed users, each of size $L \in \mathbb{N}$, trained on their local data, in a privacy-preserving manner. SwiftAgg+ can significantly reduce the communication overheads without any compromise on security, and achieve the optimum communication load within a diminishing gap. Specifically, in presence of at most $D$ dropout users, SwiftAgg+ achieves average per-user communication load of $(1+\mathcal{O}(\frac{1}{N}))L$ and the server communication load of $(1+\mathcal{O}(\frac{1}{N}))L$, with a worst-case information-theoretic security guarantee, against any subset of up to $T$ semi-honest users who may also collude with the curious server. The proposed SwiftAgg+ has also a flexibility to reduce the number of active communication links at the cost of increasing the the communication load between the users and the server. In particular, for any $K\in\mathbb{N}$, SwiftAgg+ can achieve the uplink communication load of $(1+\frac{T}{K})L$, and per-user communication load of up to $(1-\frac{1}{N})(1+\frac{T+D}{K})L$, where the number of pair-wise active connections in the network is $\frac{N}{2}(K+T+D+1)$.