\texttt{Range-Arithmetic}: Verifiable Deep Learning Inference on an Untrusted Party

Verifiable computing (VC) has gained prominence in decentralized machine learning systems, where resource-intensive tasks like deep neural network (DNN) inference are offloaded to external participants due to blockchain limitations. This creates a need to verify the correctness of outsourced computations without re-execution. We propose \texttt{Range-Arithmetic}, a novel framework for efficient and verifiable DNN inference that transforms non-arithmetic operations, such as rounding after fixed-point matrix multiplication and ReLU, into arithmetic steps verifiable using sum-check protocols and concatenated range proofs. Our approach avoids the complexity of Boolean encoding, high-degree polynomials, and large lookup tables while remaining compatible with finite-field-based proof systems. Experimental results show that our method not only matches the performance of existing approaches, but also reduces the computational cost of verifying the results, the computational effort required from the untrusted party performing the DNN inference, and the communication overhead between the two sides.

Learning to Detect Touches on Cluttered Tables

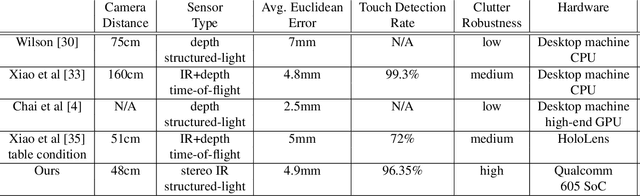
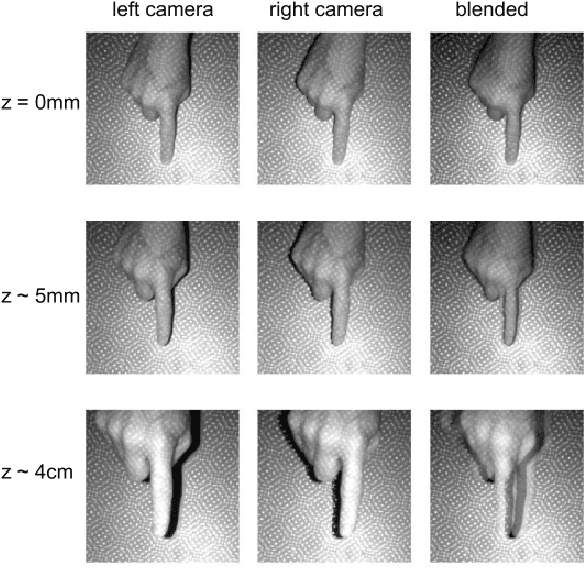
We present a novel self-contained camera-projector tabletop system with a lamp form-factor that brings digital intelligence to our tables. We propose a real-time, on-device, learning-based touch detection algorithm that makes any tabletop interactive. The top-down configuration and learning-based algorithm makes our method robust to the presence of clutter, a main limitation of existing camera-projector tabletop systems. Our research prototype enables a set of experiences that combine hand interactions and objects present on the table. A video can be found at https://youtu.be/hElC_c25Fg8.

Convergence Results for Neural Networks via Electrodynamics

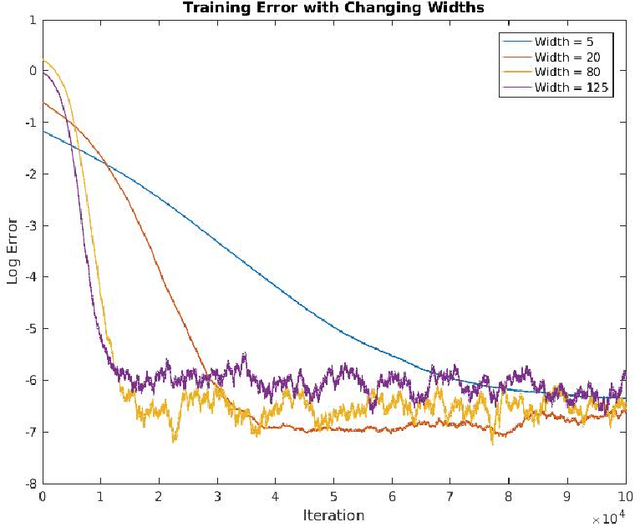
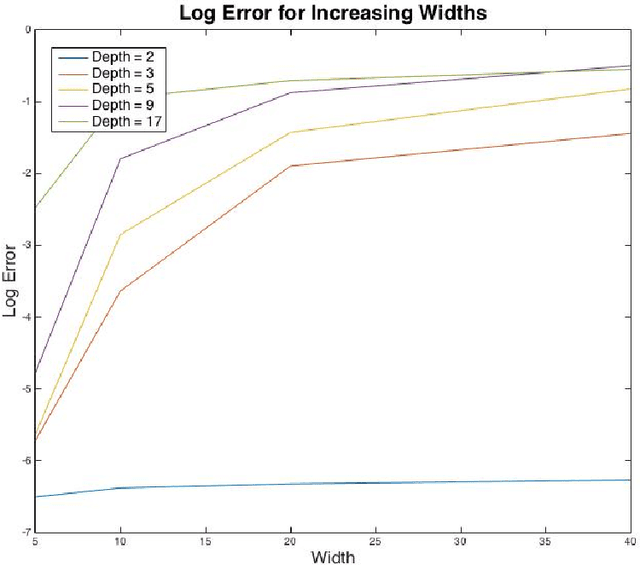
We study whether a depth two neural network can learn another depth two network using gradient descent. Assuming a linear output node, we show that the question of whether gradient descent converges to the target function is equivalent to the following question in electrodynamics: Given $k$ fixed protons in $\mathbb{R}^d,$ and $k$ electrons, each moving due to the attractive force from the protons and repulsive force from the remaining electrons, whether at equilibrium all the electrons will be matched up with the protons, up to a permutation. Under the standard electrical force, this follows from the classic Earnshaw's theorem. In our setting, the force is determined by the activation function and the input distribution. Building on this equivalence, we prove the existence of an activation function such that gradient descent learns at least one of the hidden nodes in the target network. Iterating, we show that gradient descent can be used to learn the entire network one node at a time.