Subspecialty-Specific Foundation Model for Intelligent Gastrointestinal Pathology

Gastrointestinal (GI) diseases represent a clinically significant burden, necessitating precise diagnostic approaches to optimize patient outcomes. Conventional histopathological diagnosis, heavily reliant on the subjective interpretation of pathologists, suffers from limited reproducibility and diagnostic variability. To overcome these limitations and address the lack of pathology-specific foundation models for GI diseases, we develop Digepath, a specialized foundation model for GI pathology. Our framework introduces a dual-phase iterative optimization strategy combining pretraining with fine-screening, specifically designed to address the detection of sparsely distributed lesion areas in whole-slide images. Digepath is pretrained on more than 353 million image patches from over 200,000 hematoxylin and eosin-stained slides of GI diseases. It attains state-of-the-art performance on 33 out of 34 tasks related to GI pathology, including pathological diagnosis, molecular prediction, gene mutation prediction, and prognosis evaluation, particularly in diagnostically ambiguous cases and resolution-agnostic tissue classification.We further translate the intelligent screening module for early GI cancer and achieve near-perfect 99.6% sensitivity across 9 independent medical institutions nationwide. The outstanding performance of Digepath highlights its potential to bridge critical gaps in histopathological practice. This work not only advances AI-driven precision pathology for GI diseases but also establishes a transferable paradigm for other pathology subspecialties.

On a Randomized Multi-Block ADMM for Solving Selected Machine Learning Problems

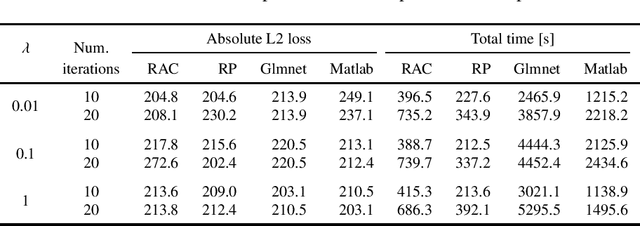
The Alternating Direction Method of Multipliers (ADMM) has now days gained tremendous attentions for solving large-scale machine learning and signal processing problems due to the relative simplicity. However, the two-block structure of the classical ADMM still limits the size of the real problems being solved. When one forces a more-than-two-block structure by variable-splitting, the convergence speed slows down greatly as observed in practice. Recently, a randomly assembled cyclic multi-block ADMM (RAC-MBADMM) was developed by the authors for solving general convex and nonconvex quadratic optimization problems where the number of blocks can go greater than two so that each sub-problem has a smaller size and can be solved much more efficiently. In this paper, we apply this method to solving few selected machine learning problems related to convex quadratic optimization, such as Linear Regression, LASSO, Elastic-Net, and SVM. We prove that the algorithm would converge in expectation linearly under the standard statistical data assumptions. We use our general-purpose solver to conduct multiple numerical tests, solving both synthetic and large-scale bench-mark problems. Our results show that RAC-MBADMM could significantly outperform, in both solution time and quality, other optimization algorithms/codes for solving these machine learning problems, and match up the performance of the best tailored methods such as Glmnet or LIBSVM. In certain problem regions RAC-MBADMM even achieves a superior performance than that of the tailored methods.