Maximizing Cumulative User Engagement in Sequential Recommendation: An Online Optimization Perspective

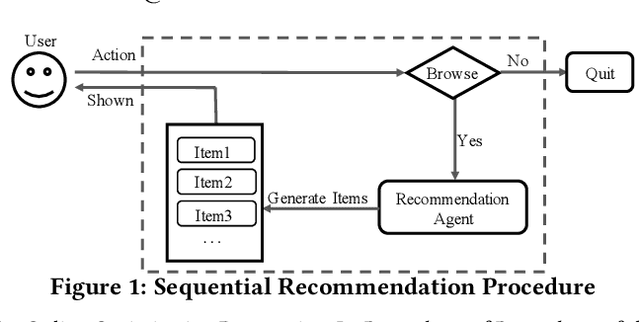
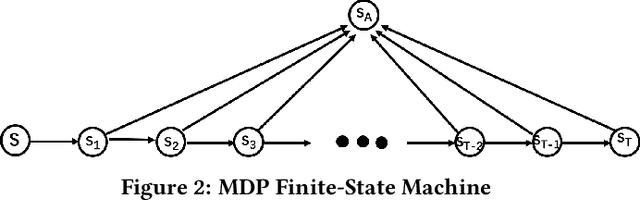
To maximize cumulative user engagement (e.g. cumulative clicks) in sequential recommendation, it is often needed to tradeoff two potentially conflicting objectives, that is, pursuing higher immediate user engagement (e.g., click-through rate) and encouraging user browsing (i.e., more items exposured). Existing works often study these two tasks separately, thus tend to result in sub-optimal results. In this paper, we study this problem from an online optimization perspective, and propose a flexible and practical framework to explicitly tradeoff longer user browsing length and high immediate user engagement. Specifically, by considering items as actions, user's requests as states and user leaving as an absorbing state, we formulate each user's behavior as a personalized Markov decision process (MDP), and the problem of maximizing cumulative user engagement is reduced to a stochastic shortest path (SSP) problem. Meanwhile, with immediate user engagement and quit probability estimation, it is shown that the SSP problem can be efficiently solved via dynamic programming. Experiments on real-world datasets demonstrate the effectiveness of the proposed approach. Moreover, this approach is deployed at a large E-commerce platform, achieved over 7% improvement of cumulative clicks.

Multinomial Logit Bandit with Linear Utility Functions

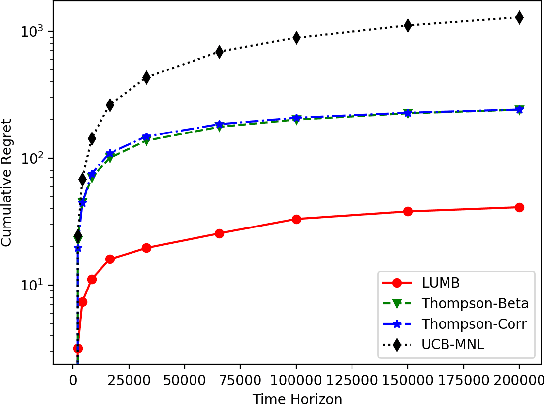
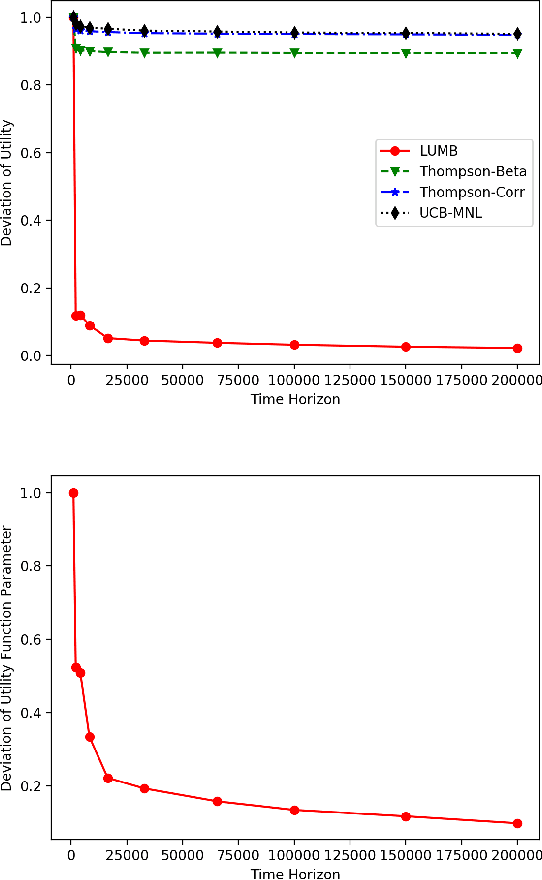
Multinomial logit bandit is a sequential subset selection problem which arises in many applications. In each round, the player selects a $K$-cardinality subset from $N$ candidate items, and receives a reward which is governed by a {\it multinomial logit} (MNL) choice model considering both item utility and substitution property among items. The player's objective is to dynamically learn the parameters of MNL model and maximize cumulative reward over a finite horizon $T$. This problem faces the exploration-exploitation dilemma, and the involved combinatorial nature makes it non-trivial. In recent years, there have developed some algorithms by exploiting specific characteristics of the MNL model, but all of them estimate the parameters of MNL model separately and incur a regret no better than $\tilde{O}\big(\sqrt{NT}\big)$ which is not preferred for large candidate set size $N$. In this paper, we consider the {\it linear utility} MNL choice model whose item utilities are represented as linear functions of $d$-dimension item features, and propose an algorithm, titled {\bf LUMB}, to exploit the underlying structure. It is proven that the proposed algorithm achieves $\tilde{O}\big(dK\sqrt{T}\big)$ regret which is free of candidate set size. Experiments show the superiority of the proposed algorithm.