Learning to Succeed while Teaching to Fail: Privacy in Closed Machine Learning Systems

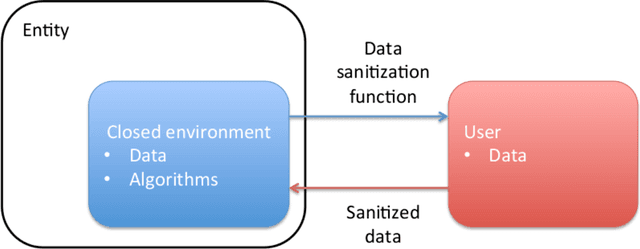
Security, privacy, and fairness have become critical in the era of data science and machine learning. More and more we see that achieving universally secure, private, and fair systems is practically impossible. We have seen for example how generative adversarial networks can be used to learn about the expected private training data; how the exploitation of additional data can reveal private information in the original one; and how what looks like unrelated features can teach us about each other. Confronted with this challenge, in this paper we open a new line of research, where the security, privacy, and fairness is learned and used in a closed environment. The goal is to ensure that a given entity (e.g., the company or the government), trusted to infer certain information with our data, is blocked from inferring protected information from it. For example, a hospital might be allowed to produce diagnosis on the patient (the positive task), without being able to infer the gender of the subject (negative task). Similarly, a company can guarantee that internally it is not using the provided data for any undesired task, an important goal that is not contradicting the virtually impossible challenge of blocking everybody from the undesired task. We design a system that learns to succeed on the positive task while simultaneously fail at the negative one, and illustrate this with challenging cases where the positive task is actually harder than the negative one being blocked. Fairness, to the information in the negative task, is often automatically obtained as a result of this proposed approach. The particular framework and examples open the door to security, privacy, and fairness in very important closed scenarios, ranging from private data accumulation companies like social networks to law-enforcement and hospitals.

Robust Large Margin Deep Neural Networks

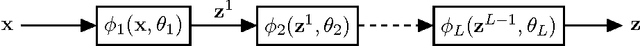
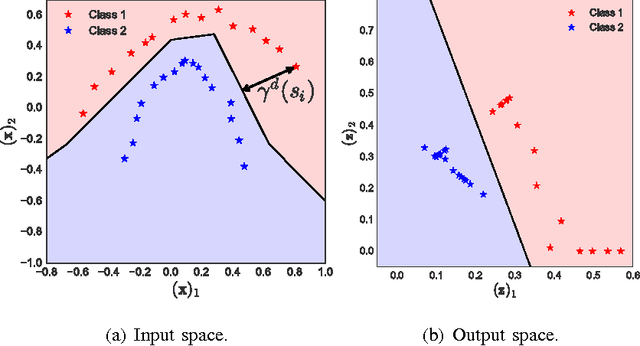
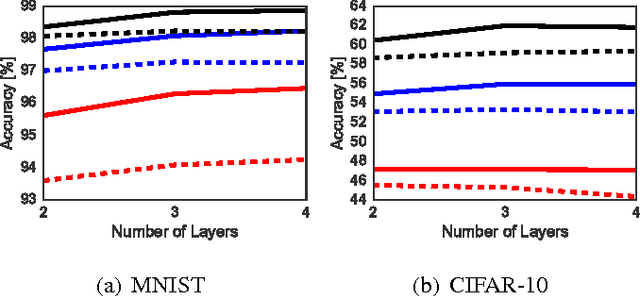
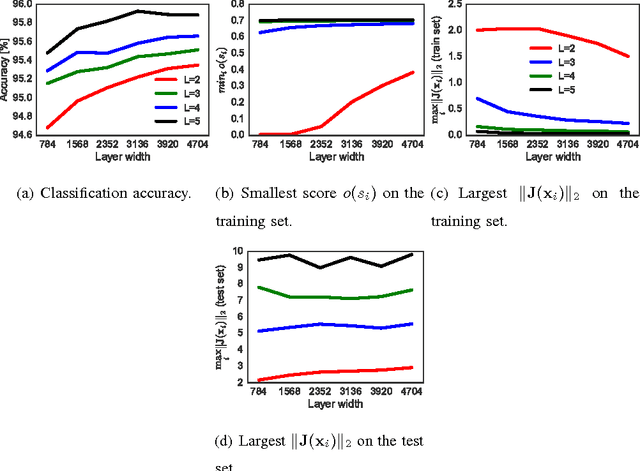
The generalization error of deep neural networks via their classification margin is studied in this work. Our approach is based on the Jacobian matrix of a deep neural network and can be applied to networks with arbitrary non-linearities and pooling layers, and to networks with different architectures such as feed forward networks and residual networks. Our analysis leads to the conclusion that a bounded spectral norm of the network's Jacobian matrix in the neighbourhood of the training samples is crucial for a deep neural network of arbitrary depth and width to generalize well. This is a significant improvement over the current bounds in the literature, which imply that the generalization error grows with either the width or the depth of the network. Moreover, it shows that the recently proposed batch normalization and weight normalization re-parametrizations enjoy good generalization properties, and leads to a novel network regularizer based on the network's Jacobian matrix. The analysis is supported with experimental results on the MNIST, CIFAR-10, LaRED and ImageNet datasets.

Bounds on the Number of Measurements for Reliable Compressive Classification

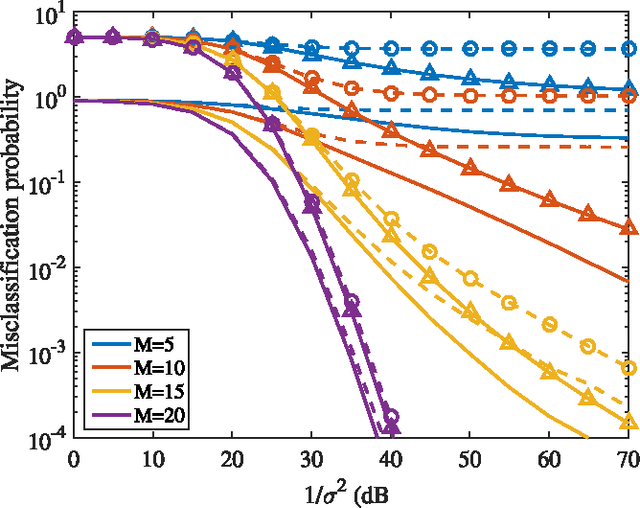
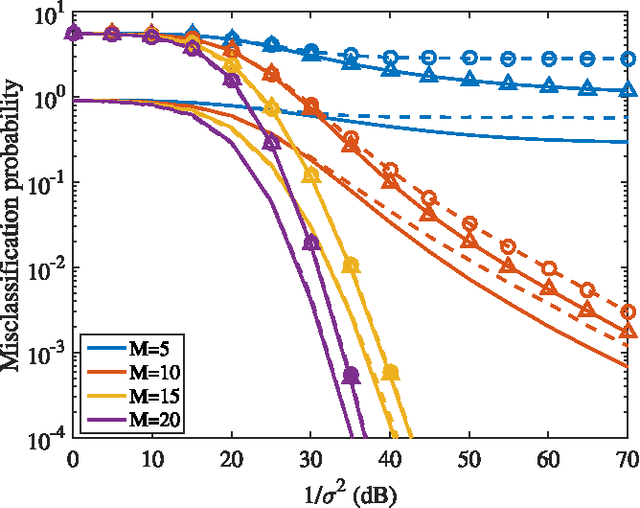
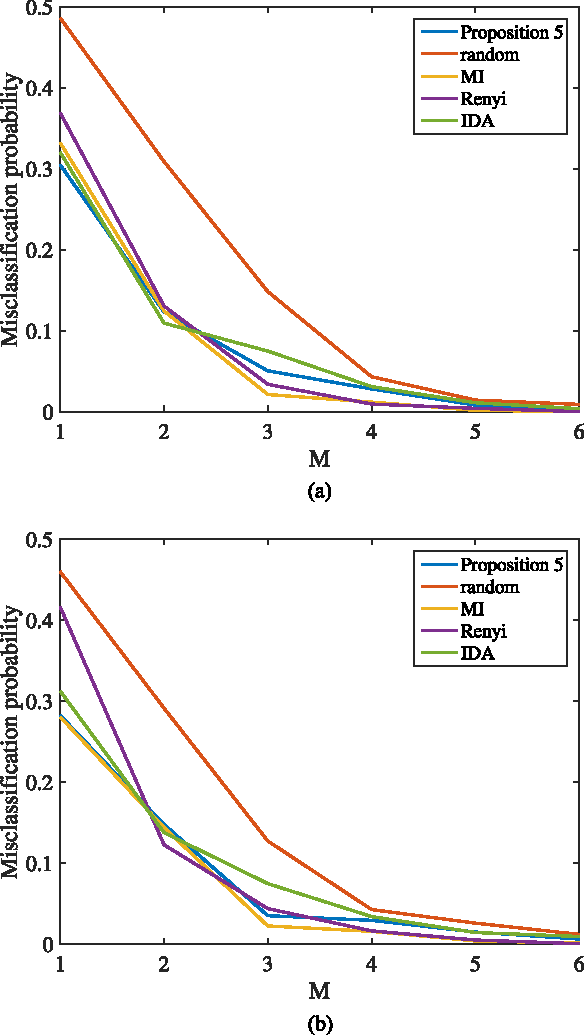
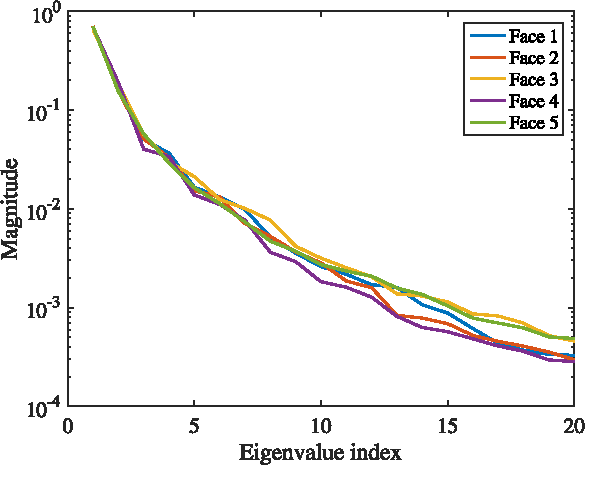
This paper studies the classification of high-dimensional Gaussian signals from low-dimensional noisy, linear measurements. In particular, it provides upper bounds (sufficient conditions) on the number of measurements required to drive the probability of misclassification to zero in the low-noise regime, both for random measurements and designed ones. Such bounds reveal two important operational regimes that are a function of the characteristics of the source: i) when the number of classes is less than or equal to the dimension of the space spanned by signals in each class, reliable classification is possible in the low-noise regime by using a one-vs-all measurement design; ii) when the dimension of the spaces spanned by signals in each class is lower than the number of classes, reliable classification is guaranteed in the low-noise regime by using a simple random measurement design. Simulation results both with synthetic and real data show that our analysis is sharp, in the sense that it is able to gauge the number of measurements required to drive the misclassification probability to zero in the low-noise regime.

Multi-modal dictionary learning for image separation with application in art investigation

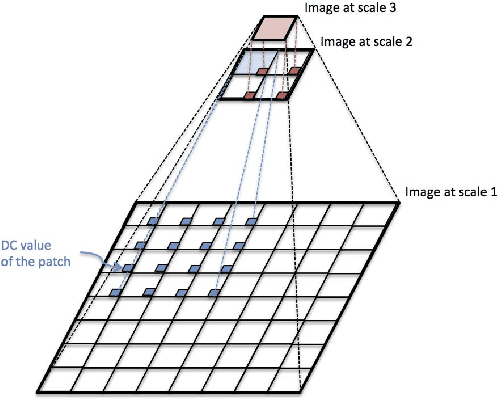
In support of art investigation, we propose a new source separation method that unmixes a single X-ray scan acquired from double-sided paintings. In this problem, the X-ray signals to be separated have similar morphological characteristics, which brings previous source separation methods to their limits. Our solution is to use photographs taken from the front and back-side of the panel to drive the separation process. The crux of our approach relies on the coupling of the two imaging modalities (photographs and X-rays) using a novel coupled dictionary learning framework able to capture both common and disparate features across the modalities using parsimonious representations; the common component models features shared by the multi-modal images, whereas the innovation component captures modality-specific information. As such, our model enables the formulation of appropriately regularized convex optimization procedures that lead to the accurate separation of the X-rays. Our dictionary learning framework can be tailored both to a single- and a multi-scale framework, with the latter leading to a significant performance improvement. Moreover, to improve further on the visual quality of the separated images, we propose to train coupled dictionaries that ignore certain parts of the painting corresponding to craquelure. Experimentation on synthetic and real data - taken from digital acquisition of the Ghent Altarpiece (1432) - confirms the superiority of our method against the state-of-the-art morphological component analysis technique that uses either fixed or trained dictionaries to perform image separation.

X-ray image separation via coupled dictionary learning

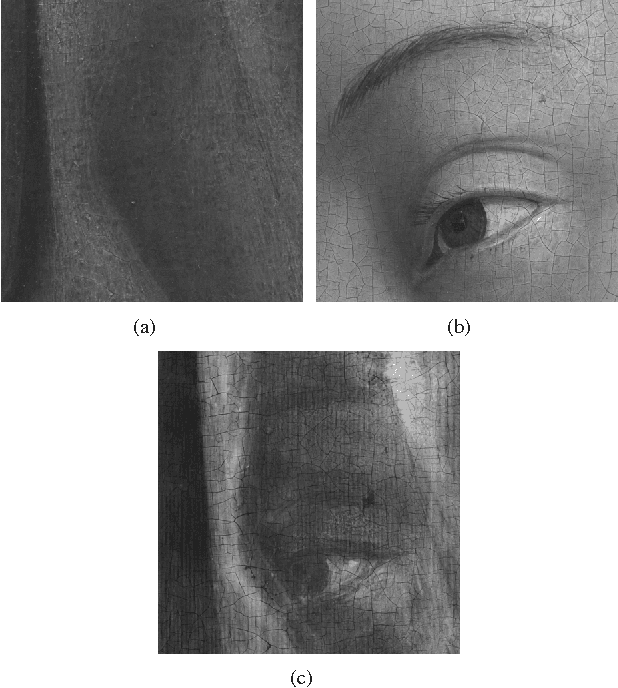
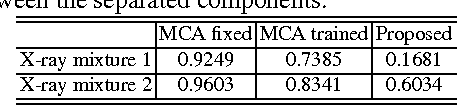
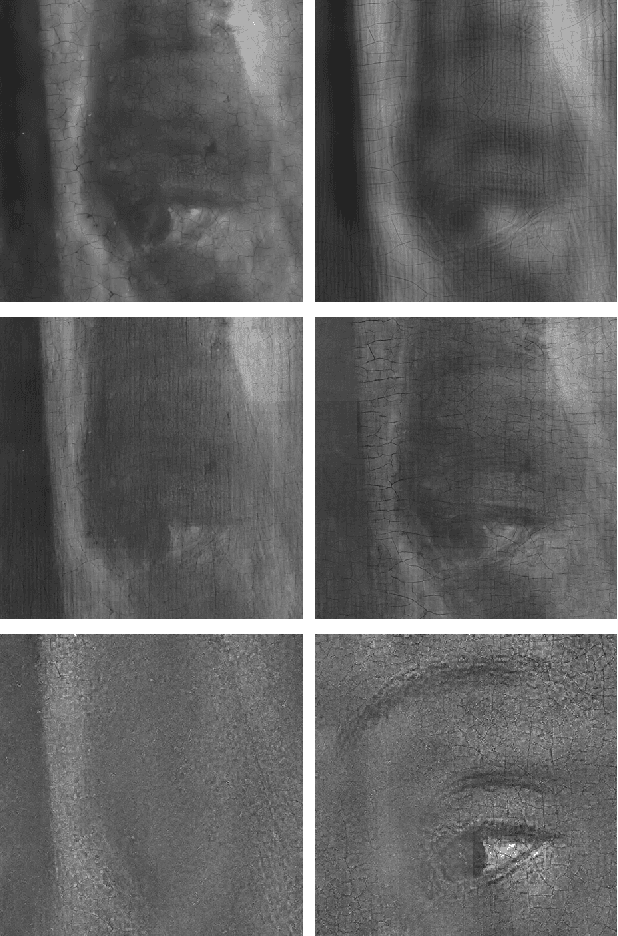
In support of art investigation, we propose a new source sepa- ration method that unmixes a single X-ray scan acquired from double-sided paintings. Unlike prior source separation meth- ods, which are based on statistical or structural incoherence of the sources, we use visual images taken from the front- and back-side of the panel to drive the separation process. The coupling of the two imaging modalities is achieved via a new multi-scale dictionary learning method. Experimental results demonstrate that our method succeeds in the discrimination of the sources, while state-of-the-art methods fail to do so.

Classification and Reconstruction of High-Dimensional Signals from Low-Dimensional Features in the Presence of Side Information

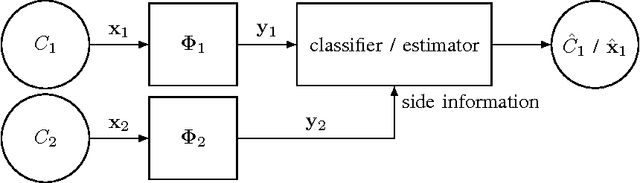
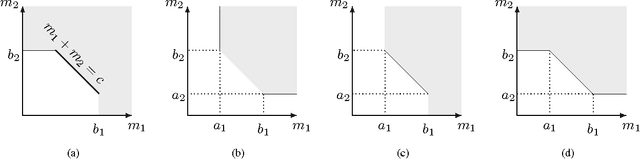
This paper offers a characterization of fundamental limits on the classification and reconstruction of high-dimensional signals from low-dimensional features, in the presence of side information. We consider a scenario where a decoder has access both to linear features of the signal of interest and to linear features of the side information signal; while the side information may be in a compressed form, the objective is recovery or classification of the primary signal, not the side information. The signal of interest and the side information are each assumed to have (distinct) latent discrete labels; conditioned on these two labels, the signal of interest and side information are drawn from a multivariate Gaussian distribution. With joint probabilities on the latent labels, the overall signal-(side information) representation is defined by a Gaussian mixture model. We then provide sharp sufficient and/or necessary conditions for these quantities to approach zero when the covariance matrices of the Gaussians are nearly low-rank. These conditions, which are reminiscent of the well-known Slepian-Wolf and Wyner-Ziv conditions, are a function of the number of linear features extracted from the signal of interest, the number of linear features extracted from the side information signal, and the geometry of these signals and their interplay. Moreover, on assuming that the signal of interest and the side information obey such an approximately low-rank model, we derive expansions of the reconstruction error as a function of the deviation from an exactly low-rank model; such expansions also allow identification of operational regimes where the impact of side information on signal reconstruction is most relevant. Our framework, which offers a principled mechanism to integrate side information in high-dimensional data problems, is also tested in the context of imaging applications.

Mismatch in the Classification of Linear Subspaces: Sufficient Conditions for Reliable Classification

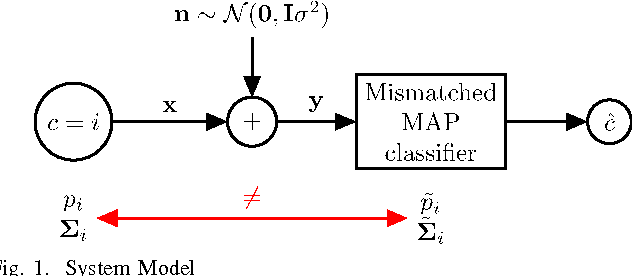
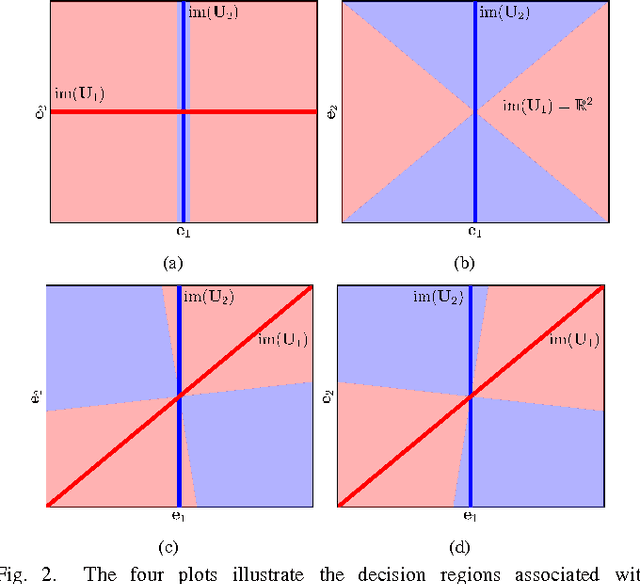
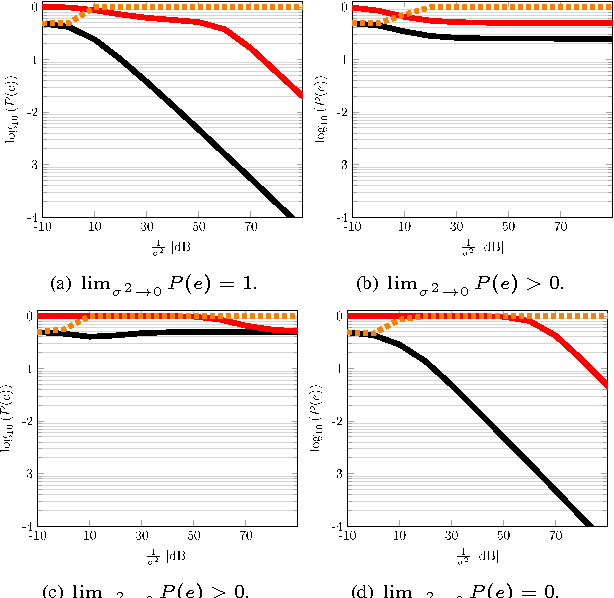
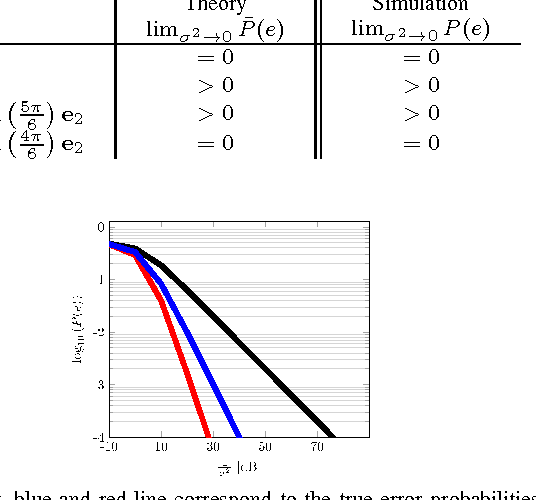
This paper considers the classification of linear subspaces with mismatched classifiers. In particular, we assume a model where one observes signals in the presence of isotropic Gaussian noise and the distribution of the signals conditioned on a given class is Gaussian with a zero mean and a low-rank covariance matrix. We also assume that the classifier knows only a mismatched version of the parameters of input distribution in lieu of the true parameters. By constructing an asymptotic low-noise expansion of an upper bound to the error probability of such a mismatched classifier, we provide sufficient conditions for reliable classification in the low-noise regime that are able to sharply predict the absence of a classification error floor. Such conditions are a function of the geometry of the true signal distribution, the geometry of the mismatched signal distributions as well as the interplay between such geometries, namely, the principal angles and the overlap between the true and the mismatched signal subspaces. Numerical results demonstrate that our conditions for reliable classification can sharply predict the behavior of a mismatched classifier both with synthetic data and in a motion segmentation and a hand-written digit classification applications.

Adaptive-Rate Sparse Signal Reconstruction With Application in Compressive Background Subtraction

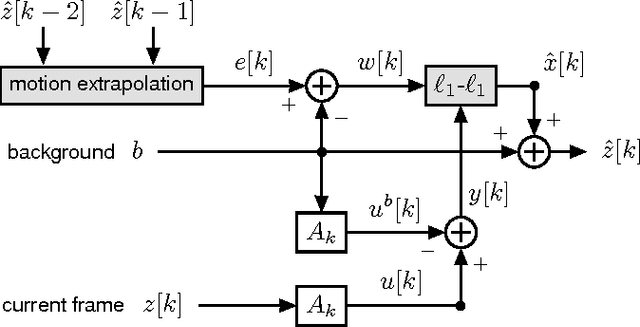
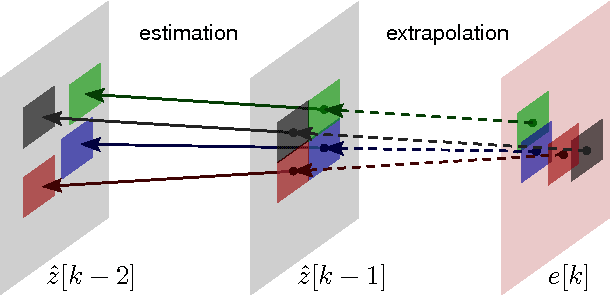
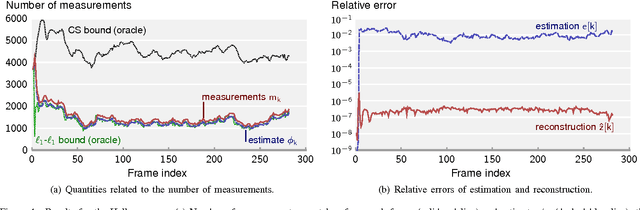
We propose and analyze an online algorithm for reconstructing a sequence of signals from a limited number of linear measurements. The signals are assumed sparse, with unknown support, and evolve over time according to a generic nonlinear dynamical model. Our algorithm, based on recent theoretical results for $\ell_1$-$\ell_1$ minimization, is recursive and computes the number of measurements to be taken at each time on-the-fly. As an example, we apply the algorithm to compressive video background subtraction, a problem that can be stated as follows: given a set of measurements of a sequence of images with a static background, simultaneously reconstruct each image while separating its foreground from the background. The performance of our method is illustrated on sequences of real images: we observe that it allows a dramatic reduction in the number of measurements with respect to state-of-the-art compressive background subtraction schemes.

Compressed Sensing With Side Information: Geometrical Interpretation and Performance Bounds

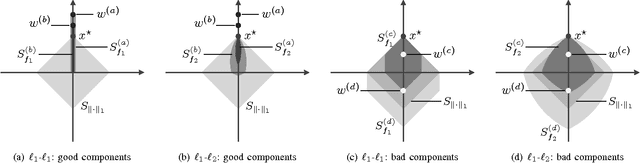
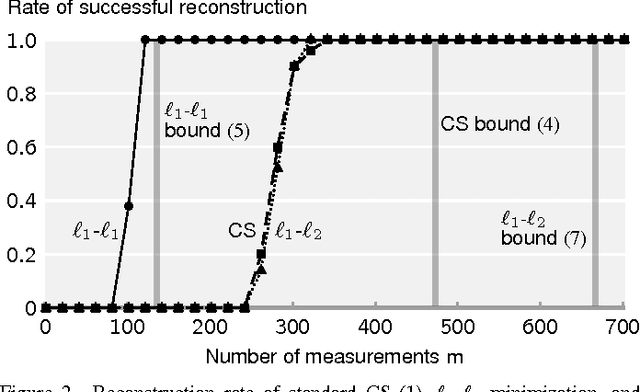
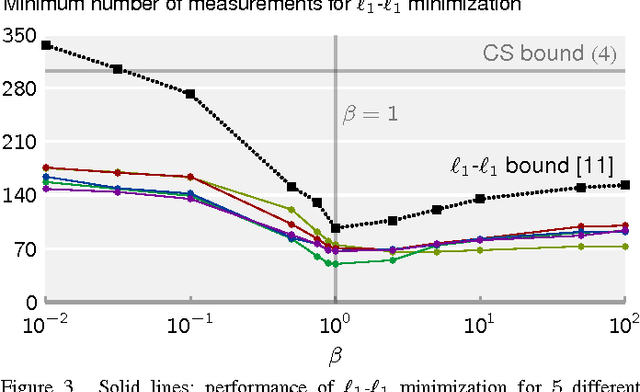
We address the problem of Compressed Sensing (CS) with side information. Namely, when reconstructing a target CS signal, we assume access to a similar signal. This additional knowledge, the side information, is integrated into CS via L1-L1 and L1-L2 minimization. We then provide lower bounds on the number of measurements that these problems require for successful reconstruction of the target signal. If the side information has good quality, the number of measurements is significantly reduced via L1-L1 minimization, but not so much via L1-L2 minimization. We provide geometrical interpretations and experimental results illustrating our findings.