Image Separation with Side Information: A Connected Auto-Encoders Based Approach

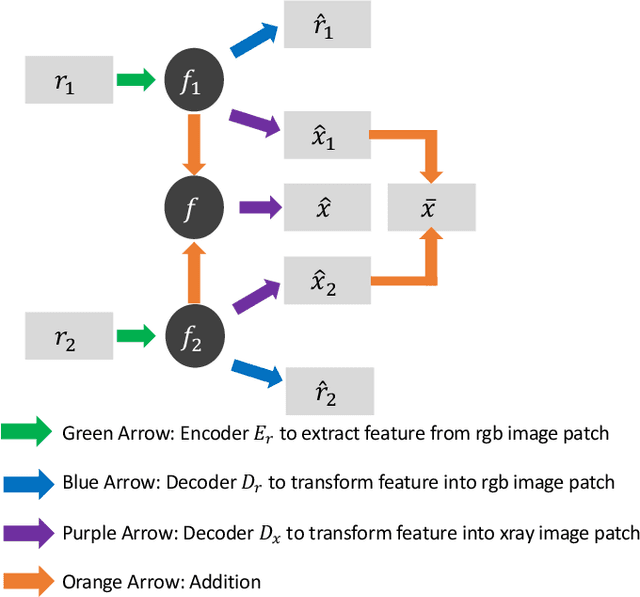
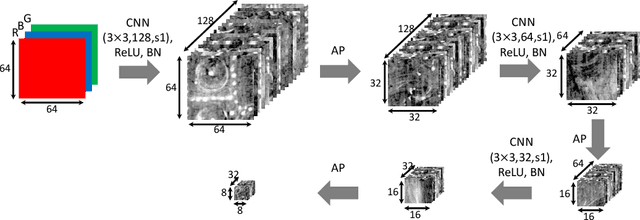
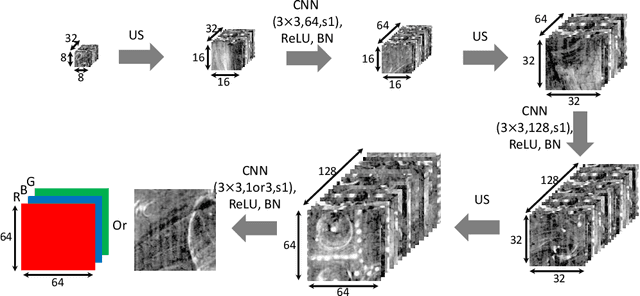
X-radiography (X-ray imaging) is a widely used imaging technique in art investigation. It can provide information about the condition of a painting as well as insights into an artist's techniques and working methods, often revealing hidden information invisible to the naked eye. In this paper, we deal with the problem of separating mixed X-ray images originating from the radiography of double-sided paintings. Using the visible color images (RGB images) from each side of the painting, we propose a new Neural Network architecture, based upon 'connected' auto-encoders, designed to separate the mixed X-ray image into two simulated X-ray images corresponding to each side. In this proposed architecture, the convolutional auto encoders extract features from the RGB images. These features are then used to (1) reproduce both of the original RGB images, (2) reconstruct the hypothetical separated X-ray images, and (3) regenerate the mixed X-ray image. The algorithm operates in a totally self-supervised fashion without requiring a sample set that contains both the mixed X-ray images and the separated ones. The methodology was tested on images from the double-sided wing panels of the \textsl{Ghent Altarpiece}, painted in 1432 by the brothers Hubert and Jan van Eyck. These tests show that the proposed approach outperforms other state-of-the-art X-ray image separation methods for art investigation applications.

Model-Aware Regularization For Learning Approaches To Inverse Problems

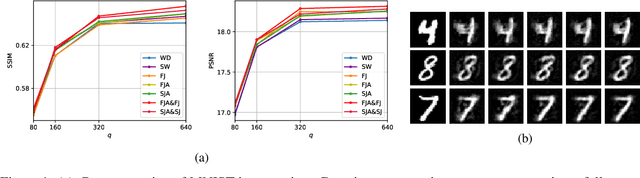
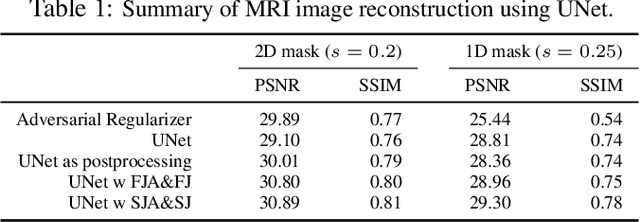
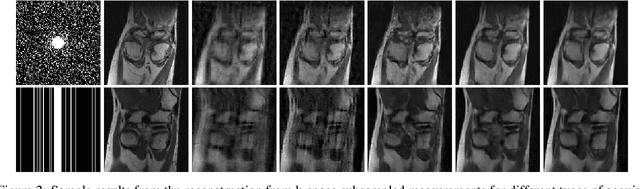
There are various inverse problems -- including reconstruction problems arising in medical imaging -- where one is often aware of the forward operator that maps variables of interest to the observations. It is therefore natural to ask whether such knowledge of the forward operator can be exploited in deep learning approaches increasingly used to solve inverse problems. In this paper, we provide one such way via an analysis of the generalisation error of deep learning methods applicable to inverse problems. In particular, by building on the algorithmic robustness framework, we offer a generalisation error bound that encapsulates key ingredients associated with the learning problem such as the complexity of the data space, the size of the training set, the Jacobian of the deep neural network and the Jacobian of the composition of the forward operator with the neural network. We then propose a 'plug-and-play' regulariser that leverages the knowledge of the forward map to improve the generalization of the network. We likewise also propose a new method allowing us to tightly upper bound the Lipschitz constants of the relevant functions that is much more computational efficient than existing ones. We demonstrate the efficacy of our model-aware regularised deep learning algorithms against other state-of-the-art approaches on inverse problems involving various sub-sampling operators such as those used in classical compressed sensing setup and accelerated Magnetic Resonance Imaging (MRI).

Lautum Regularization for Semi-supervised Transfer Learning

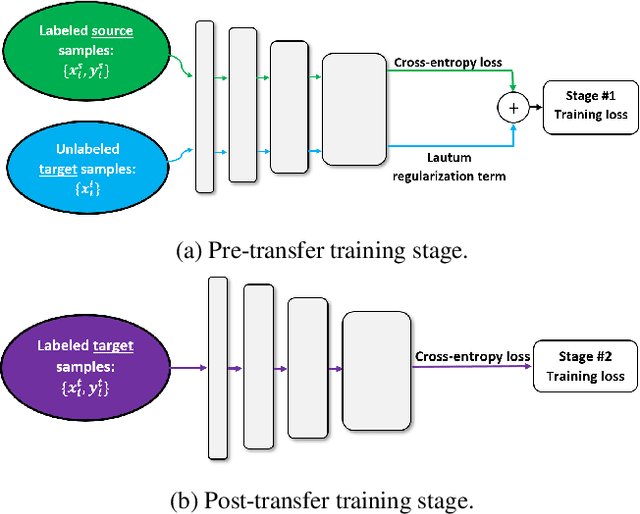
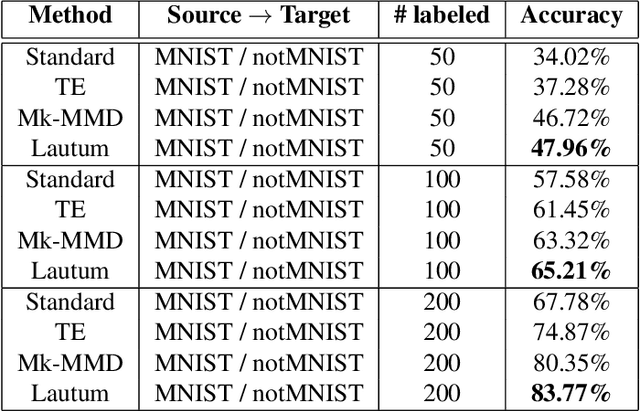
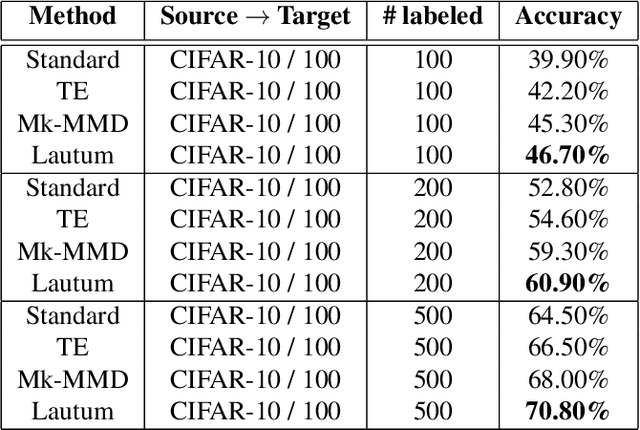
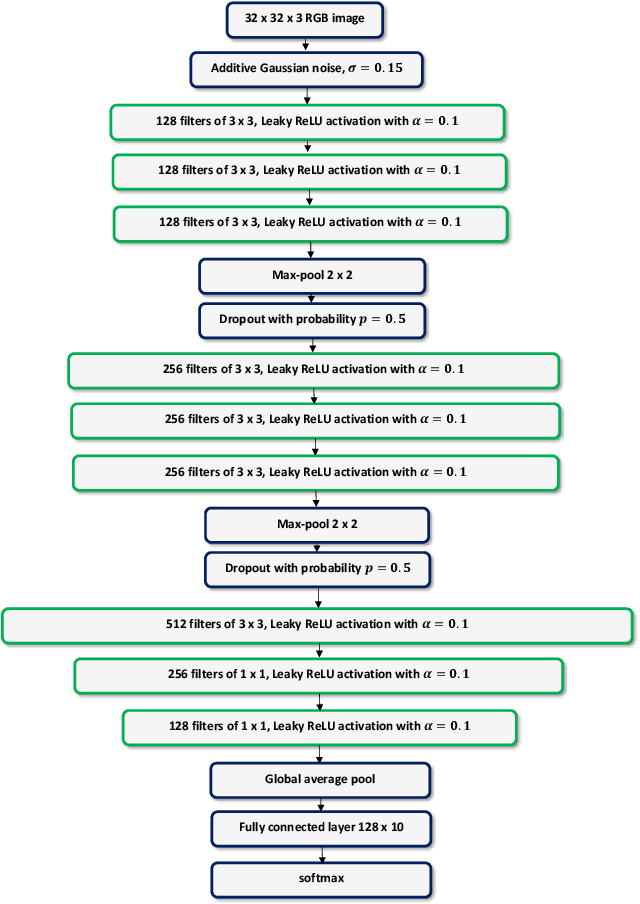
Transfer learning is a very important tool in deep learning as it allows propagating information from one "source dataset" to another "target dataset", especially in the case of a small number of training examples in the latter. Yet, discrepancies between the underlying distributions of the source and target data are commonplace and are known to have a substantial impact on algorithm performance. In this work we suggest a novel information theoretic approach for the analysis of the performance of deep neural networks in the context of transfer learning. We focus on the task of semi-supervised transfer learning, in which unlabeled samples from the target dataset are available during the network training on the source dataset. Our theory suggests that one may improve the transferability of a deep neural network by imposing a Lautum information based regularization that relates the network weights to the target data. We demonstrate in various transfer learning experiments the effectiveness of the proposed approach.

Deep Learning for Inverse Problems: Bounds and Regularizers

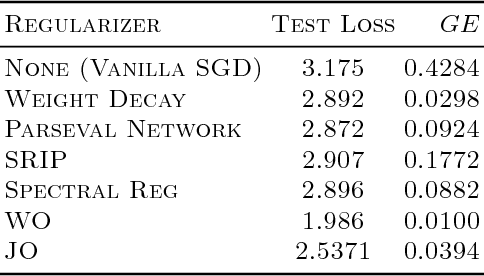
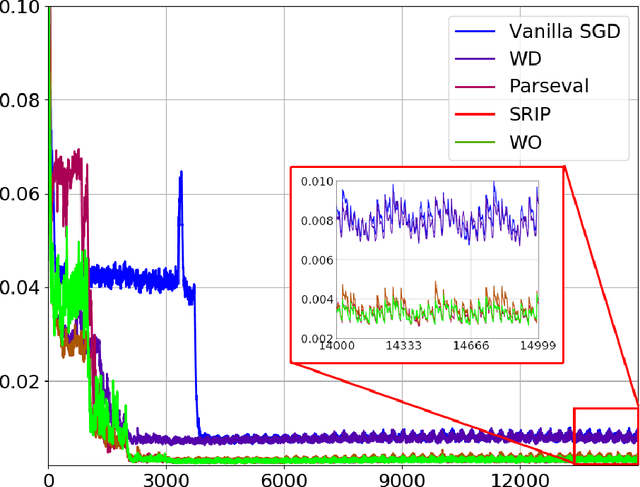
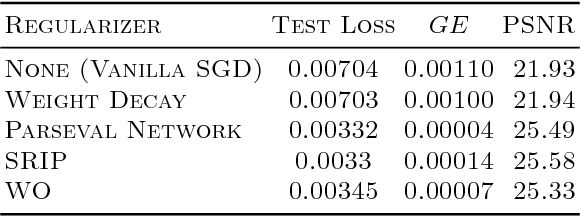
Inverse problems arise in a number of domains such as medical imaging, remote sensing, and many more, relying on the use of advanced signal and image processing approaches -- such as sparsity-driven techniques -- to determine their solution. This paper instead studies the use of deep learning approaches to approximate the solution of inverse problems. In particular, the paper provides a new generalization bound, depending on key quantity associated with a deep neural network -- its Jacobian matrix -- that also leads to a number of computationally efficient regularization strategies applicable to inverse problems. The paper also tests the proposed regularization strategies in a number of inverse problems including image super-resolution ones. Our numerical results conducted on various datasets show that both fully connected and convolutional neural networks regularized using the regularization or proxy regularization strategies originating from our theory exhibit much better performance than deep networks regularized with standard approaches such as weight-decay.

Generalization Error in Deep Learning

Deep learning models have lately shown great performance in various fields such as computer vision, speech recognition, speech translation, and natural language processing. However, alongside their state-of-the-art performance, it is still generally unclear what is the source of their generalization ability. Thus, an important question is what makes deep neural networks able to generalize well from the training set to new data. In this article, we provide an overview of the existing theory and bounds for the characterization of the generalization error of deep neural networks, combining both classical and more recent theoretical and empirical results.

Coupled Dictionary Learning for Multi-contrast MRI Reconstruction

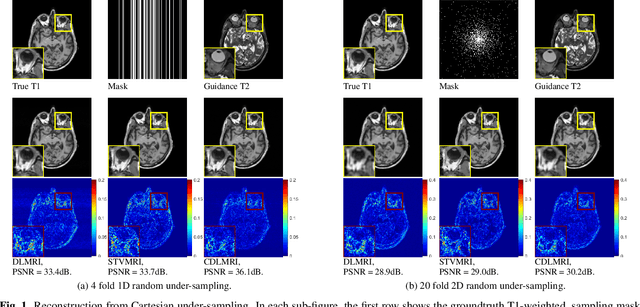
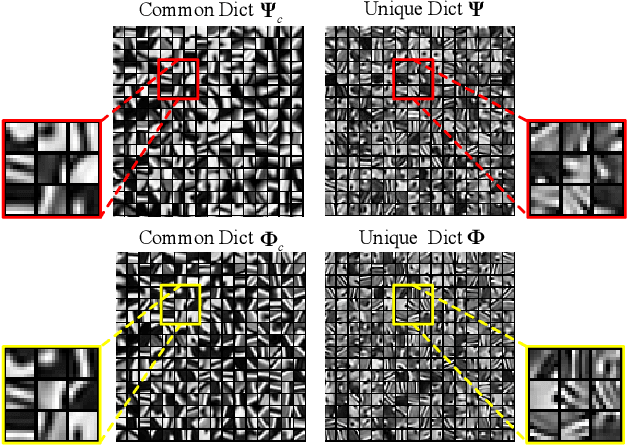
Medical imaging tasks often involve multiple contrasts, such as T1- and T2-weighted magnetic resonance imaging (MRI) data. These contrasts capture information associated with the same underlying anatomy and thus exhibit similarities. In this paper, we propose a Coupled Dictionary Learning based multi-contrast MRI reconstruction (CDLMRI) approach to leverage an available guidance contrast to restore the target contrast. Our approach consists of three stages: coupled dictionary learning, coupled sparse denoising, and $k$-space consistency enforcing. The first stage learns a group of dictionaries that capture correlations among multiple contrasts. By capitalizing on the learned adaptive dictionaries, the second stage performs joint sparse coding to denoise the corrupted target image with the aid of a guidance contrast. The third stage enforces consistency between the denoised image and the measurements in the $k$-space domain. Numerical experiments on the retrospective under-sampling of clinical MR images demonstrate that incorporating additional guidance contrast via our design improves MRI reconstruction, compared to state-of-the-art approaches.

Multimodal Image Denoising based on Coupled Dictionary Learning

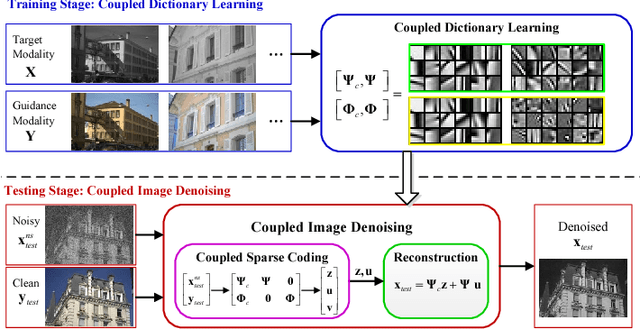
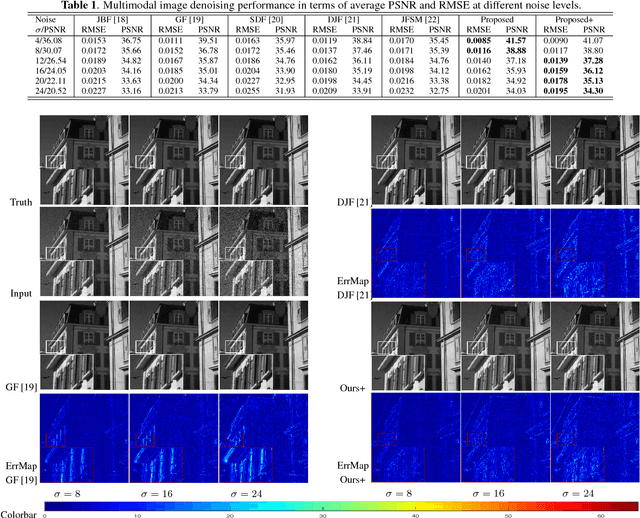
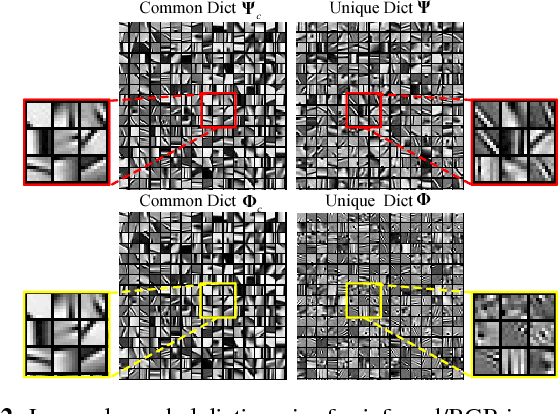
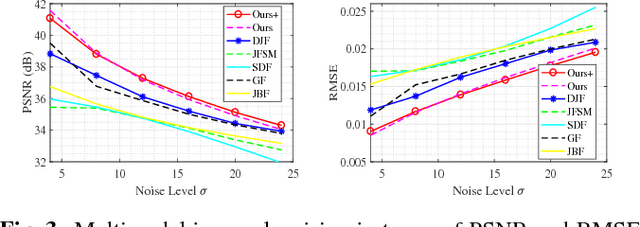
In this paper, we propose a new multimodal image denoising approach to attenuate white Gaussian additive noise in a given image modality under the aid of a guidance image modality. The proposed coupled image denoising approach consists of two stages: coupled sparse coding and reconstruction. The first stage performs joint sparse transform for multimodal images with respect to a group of learned coupled dictionaries, followed by a shrinkage operation on the sparse representations. Then, in the second stage, the shrunken representations, together with coupled dictionaries, contribute to the reconstruction of the denoised image via an inverse transform. The proposed denoising scheme demonstrates the capability to capture both the common and distinct features of different data modalities. This capability makes our approach more robust to inconsistencies between the guidance and the target images, thereby overcoming drawbacks such as the texture copying artifacts. Experiments on real multimodal images demonstrate that the proposed approach is able to better employ guidance information to bring notable benefits in the image denoising task with respect to the state-of-the-art.

Multi-modal Image Processing based on Coupled Dictionary Learning

In real-world scenarios, many data processing problems often involve heterogeneous images associated with different imaging modalities. Since these multimodal images originate from the same phenomenon, it is realistic to assume that they share common attributes or characteristics. In this paper, we propose a multi-modal image processing framework based on coupled dictionary learning to capture similarities and disparities between different image modalities. In particular, our framework can capture favorable structure similarities across different image modalities such as edges, corners, and other elementary primitives in a learned sparse transform domain, instead of the original pixel domain, that can be used to improve a number of image processing tasks such as denoising, inpainting, or super-resolution. Practical experiments demonstrate that incorporating multimodal information using our framework brings notable benefits.

Multimodal Image Super-resolution via Joint Sparse Representations induced by Coupled Dictionaries

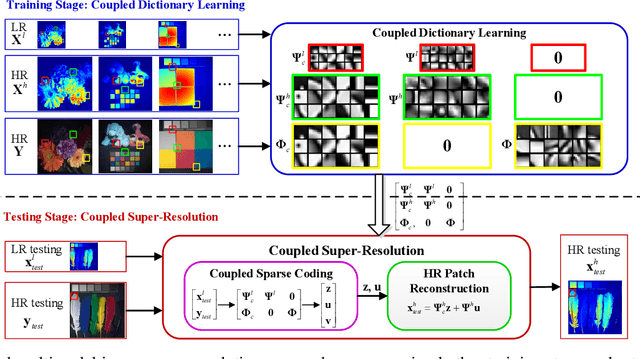
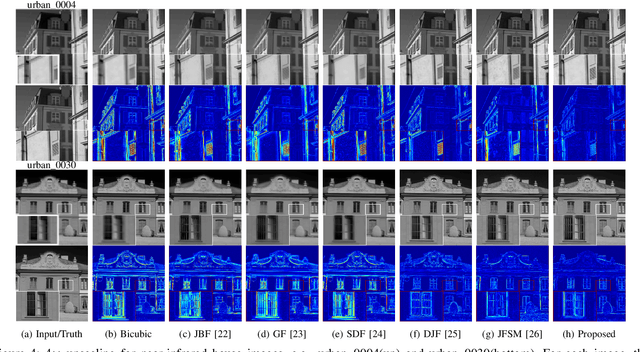
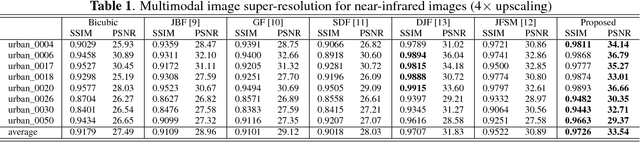
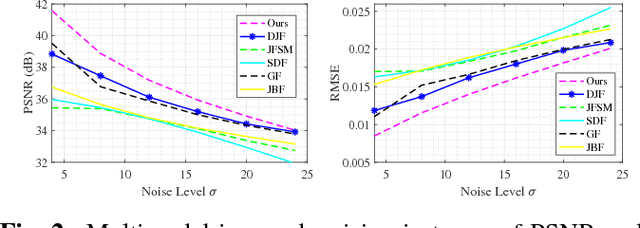
Real-world data processing problems often involve various image modalities associated with a certain scene, including RGB images, infrared images or multi-spectral images. The fact that different image modalities often share certain attributes, such as certain edges, textures and other structure primitives, represents an opportunity to enhance various image processing tasks. This paper proposes a new approach to construct a high-resolution (HR) version of a low-resolution (LR) image given another HR image modality as reference, based on joint sparse representations induced by coupled dictionaries. Our approach, which captures the similarities and disparities between different image modalities in a learned sparse feature domain in \emph{lieu} of the original image domain, consists of two phases. The coupled dictionary learning phase is used to learn a set of dictionaries that couple different image modalities in the sparse feature domain given a set of training data. In turn, the coupled super-resolution phase leverages such coupled dictionaries to construct a HR version of the LR target image given another related image modality. One of the merits of our sparsity-driven approach relates to the fact that it overcomes drawbacks such as the texture copying artifacts commonly resulting from inconsistency between the guidance and target images. Experiments on real multimodal images demonstrate that incorporating appropriate guidance information via joint sparse representation induced by coupled dictionary learning brings notable benefits in the super-resolution task with respect to the state-of-the-art. Of particular relevance, the proposed approach also demonstrates better robustness than competing deep-learning-based methods in the presence of noise.

Generalization Error of Invariant Classifiers

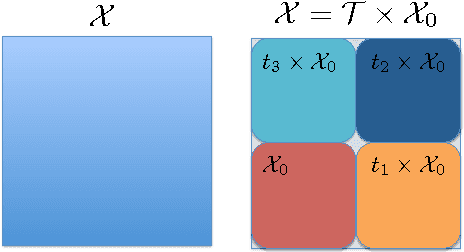
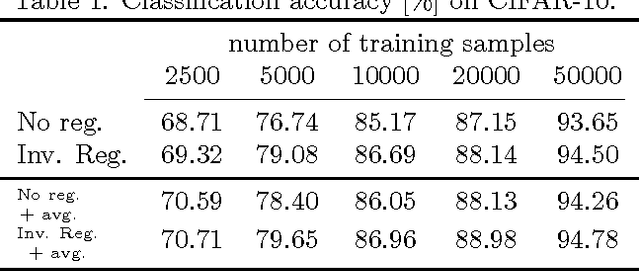
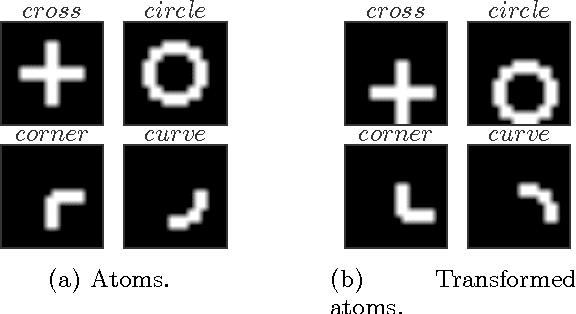
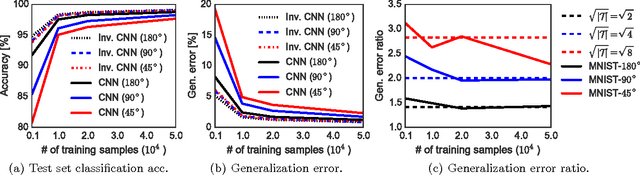
This paper studies the generalization error of invariant classifiers. In particular, we consider the common scenario where the classification task is invariant to certain transformations of the input, and that the classifier is constructed (or learned) to be invariant to these transformations. Our approach relies on factoring the input space into a product of a base space and a set of transformations. We show that whereas the generalization error of a non-invariant classifier is proportional to the complexity of the input space, the generalization error of an invariant classifier is proportional to the complexity of the base space. We also derive a set of sufficient conditions on the geometry of the base space and the set of transformations that ensure that the complexity of the base space is much smaller than the complexity of the input space. Our analysis applies to general classifiers such as convolutional neural networks. We demonstrate the implications of the developed theory for such classifiers with experiments on the MNIST and CIFAR-10 datasets.