A Partitioned Sparse Variational Gaussian Process for Fast, Distributed Spatial Modeling

The next generation of Department of Energy supercomputers will be capable of exascale computation. For these machines, far more computation will be possible than that which can be saved to disk. As a result, users will be unable to rely on post-hoc access to data for uncertainty quantification and other statistical analyses and there will be an urgent need for sophisticated machine learning algorithms which can be trained in situ. Algorithms deployed in this setting must be highly scalable, memory efficient and capable of handling data which is distributed across nodes as spatially contiguous partitions. One suitable approach involves fitting a sparse variational Gaussian process (SVGP) model independently and in parallel to each spatial partition. The resulting model is scalable, efficient and generally accurate, but produces the undesirable effect of constructing discontinuous response surfaces due to the disagreement between neighboring models at their shared boundary. In this paper, we extend this idea by allowing for a small amount of communication between neighboring spatial partitions which encourages better alignment of the local models, leading to smoother spatial predictions and a better fit in general. Due to our decentralized communication scheme, the proposed extension remains highly scalable and adds very little overhead in terms of computation (and none, in terms of memory). We demonstrate this Partitioned SVGP (PSVGP) approach for the Energy Exascale Earth System Model (E3SM) and compare the results to the independent SVGP case.

Fast emulation of density functional theory simulations using approximate Gaussian processes

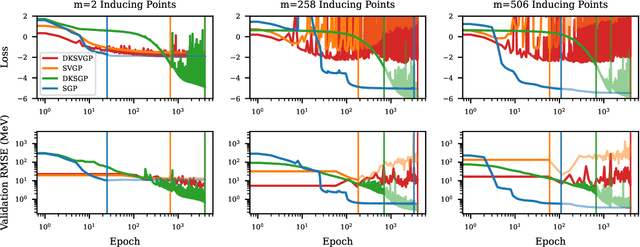
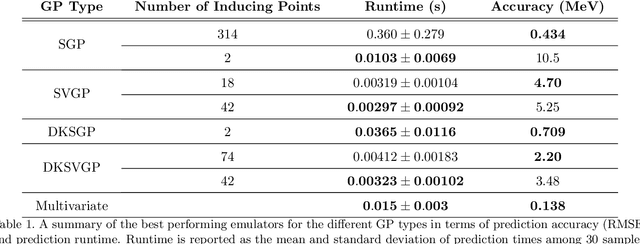
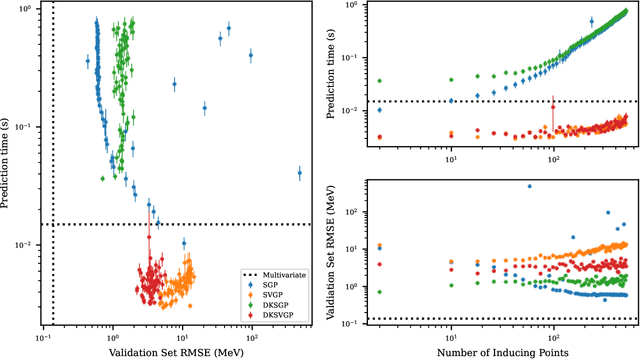
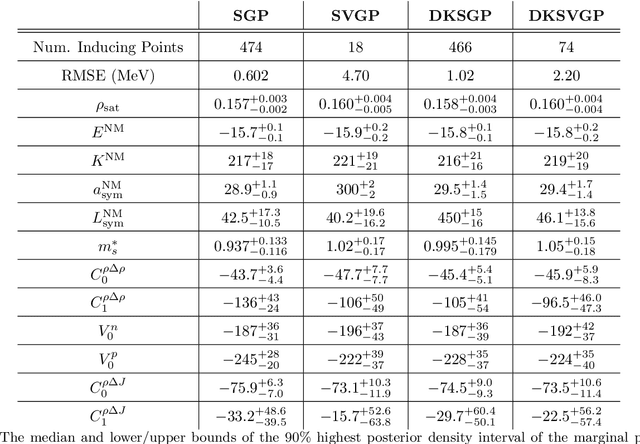
Fitting a theoretical model to experimental data in a Bayesian manner using Markov chain Monte Carlo typically requires one to evaluate the model thousands (or millions) of times. When the model is a slow-to-compute physics simulation, Bayesian model fitting becomes infeasible. To remedy this, a second statistical model that predicts the simulation output -- an "emulator" -- can be used in lieu of the full simulation during model fitting. A typical emulator of choice is the Gaussian process (GP), a flexible, non-linear model that provides both a predictive mean and variance at each input point. Gaussian process regression works well for small amounts of training data ($n < 10^3$), but becomes slow to train and use for prediction when the data set size becomes large. Various methods can be used to speed up the Gaussian process in the medium-to-large data set regime ($n > 10^5$), trading away predictive accuracy for drastically reduced runtime. This work examines the accuracy-runtime trade-off of several approximate Gaussian process models -- the sparse variational GP, stochastic variational GP, and deep kernel learned GP -- when emulating the predictions of density functional theory (DFT) models. Additionally, we use the emulators to calibrate, in a Bayesian manner, the DFT model parameters using observed data, resolving the computational barrier imposed by the data set size, and compare calibration results to previous work. The utility of these calibrated DFT models is to make predictions, based on observed data, about the properties of experimentally unobserved nuclides of interest e.g. super-heavy nuclei.