Steven Stetzler
Fast emulation of density functional theory simulations using approximate Gaussian processes
Aug 24, 2022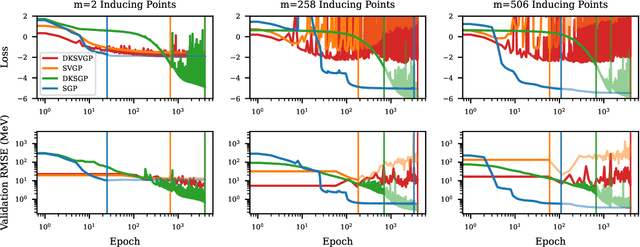
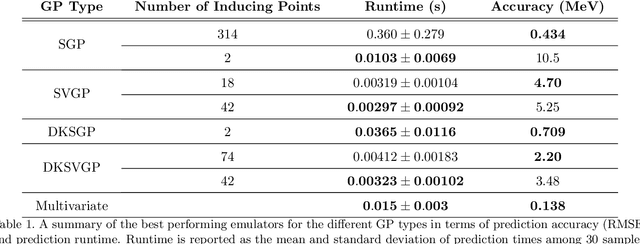
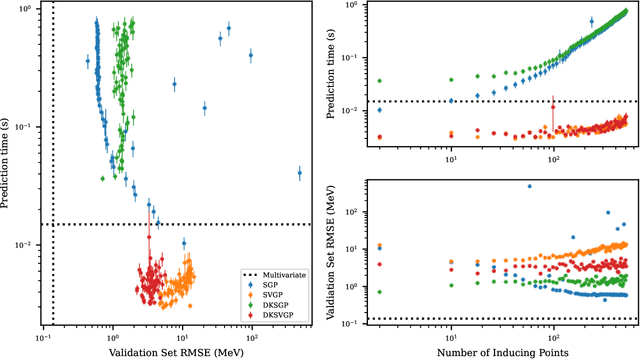
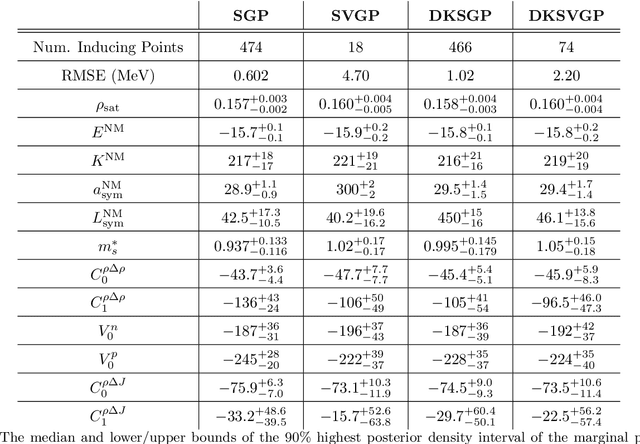
Abstract:Fitting a theoretical model to experimental data in a Bayesian manner using Markov chain Monte Carlo typically requires one to evaluate the model thousands (or millions) of times. When the model is a slow-to-compute physics simulation, Bayesian model fitting becomes infeasible. To remedy this, a second statistical model that predicts the simulation output -- an "emulator" -- can be used in lieu of the full simulation during model fitting. A typical emulator of choice is the Gaussian process (GP), a flexible, non-linear model that provides both a predictive mean and variance at each input point. Gaussian process regression works well for small amounts of training data ($n < 10^3$), but becomes slow to train and use for prediction when the data set size becomes large. Various methods can be used to speed up the Gaussian process in the medium-to-large data set regime ($n > 10^5$), trading away predictive accuracy for drastically reduced runtime. This work examines the accuracy-runtime trade-off of several approximate Gaussian process models -- the sparse variational GP, stochastic variational GP, and deep kernel learned GP -- when emulating the predictions of density functional theory (DFT) models. Additionally, we use the emulators to calibrate, in a Bayesian manner, the DFT model parameters using observed data, resolving the computational barrier imposed by the data set size, and compare calibration results to previous work. The utility of these calibrated DFT models is to make predictions, based on observed data, about the properties of experimentally unobserved nuclides of interest e.g. super-heavy nuclei.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge