Decoupling Time and Risk: Risk-Sensitive Reinforcement Learning with General Discounting

Distributional reinforcement learning (RL) is a powerful framework increasingly adopted in safety-critical domains for its ability to optimize risk-sensitive objectives. However, the role of the discount factor is often overlooked, as it is typically treated as a fixed parameter of the Markov decision process or tunable hyperparameter, with little consideration of its effect on the learned policy. In the literature, it is well-known that the discounting function plays a major role in characterizing time preferences of an agent, which an exponential discount factor cannot fully capture. Building on this insight, we propose a novel framework that supports flexible discounting of future rewards and optimization of risk measures in distributional RL. We provide a technical analysis of the optimality of our algorithms, show that our multi-horizon extension fixes issues raised with existing methodologies, and validate the robustness of our methods through extensive experiments. Our results highlight that discounting is a cornerstone in decision-making problems for capturing more expressive temporal and risk preferences profiles, with potential implications for real-world safety-critical applications.

Beyond CVaR: Leveraging Static Spectral Risk Measures for Enhanced Decision-Making in Distributional Reinforcement Learning

In domains such as finance, healthcare, and robotics, managing worst-case scenarios is critical, as failure to do so can lead to catastrophic outcomes. Distributional Reinforcement Learning (DRL) provides a natural framework to incorporate risk sensitivity into decision-making processes. However, existing approaches face two key limitations: (1) the use of fixed risk measures at each decision step often results in overly conservative policies, and (2) the interpretation and theoretical properties of the learned policies remain unclear. While optimizing a static risk measure addresses these issues, its use in the DRL framework has been limited to the simple static CVaR risk measure. In this paper, we present a novel DRL algorithm with convergence guarantees that optimizes for a broader class of static Spectral Risk Measures (SRM). Additionally, we provide a clear interpretation of the learned policy by leveraging the distribution of returns in DRL and the decomposition of static coherent risk measures. Extensive experiments demonstrate that our model learns policies aligned with the SRM objective, and outperforms existing risk-neutral and risk-sensitive DRL models in various settings.

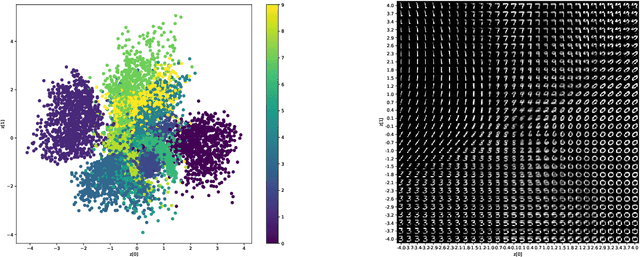
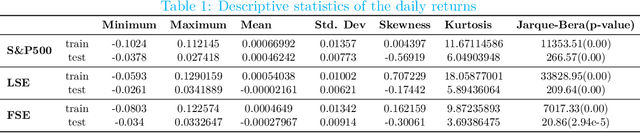
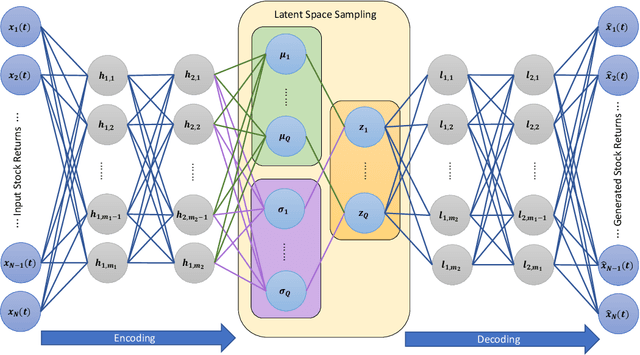
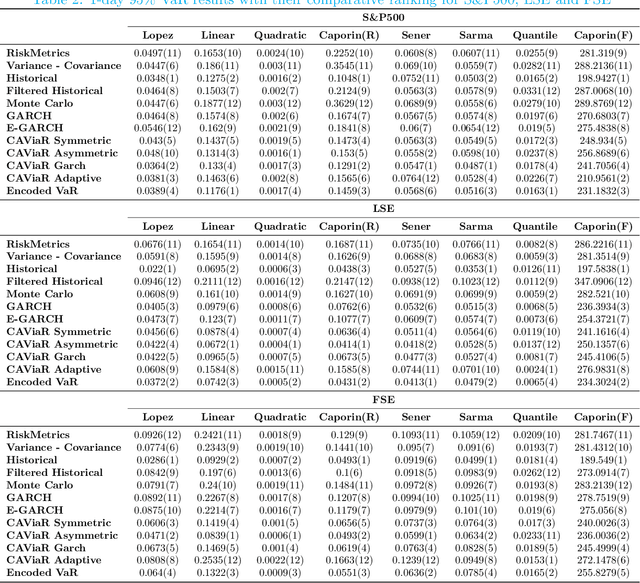
Encoded Value-at-Risk: A Predictive Machine for Financial Risk Management

Measuring risk is at the center of modern financial risk management. As the world economy is becoming more complex and standard modeling assumptions are violated, the advanced artificial intelligence solutions may provide the right tools to analyze the global market. In this paper, we provide a novel approach for measuring market risk called Encoded Value-at-Risk (Encoded VaR), which is based on a type of artificial neural network, called Variational Auto-encoders (VAEs). Encoded VaR is a generative model which can be used to reproduce market scenarios from a range of historical cross-sectional stock returns, while increasing the signal-to-noise ratio present in the financial data, and learning the dependency structure of the market without any assumptions about the joint distribution of stock returns. We compare Encoded VaR out-of-sample results with eleven other methods and show that it is competitive to many other well-known VaR algorithms presented in the literature.