Binary Excess Risk for Smooth Convex Surrogates

In statistical learning theory, convex surrogates of the 0-1 loss are highly preferred because of the computational and theoretical virtues that convexity brings in. This is of more importance if we consider smooth surrogates as witnessed by the fact that the smoothness is further beneficial both computationally- by attaining an {\it optimal} convergence rate for optimization, and in a statistical sense- by providing an improved {\it optimistic} rate for generalization bound. In this paper we investigate the smoothness property from the viewpoint of statistical consistency and show how it affects the binary excess risk. We show that in contrast to optimization and generalization errors that favor the choice of smooth surrogate loss, the smoothness of loss function may degrade the binary excess risk. Motivated by this negative result, we provide a unified analysis that integrates optimization error, generalization bound, and the error in translating convex excess risk into a binary excess risk when examining the impact of smoothness on the binary excess risk. We show that under favorable conditions appropriate choice of smooth convex loss will result in a binary excess risk that is better than $O(1/\sqrt{n})$.

Beating the Minimax Rate of Active Learning with Prior Knowledge

Active learning refers to the learning protocol where the learner is allowed to choose a subset of instances for labeling. Previous studies have shown that, compared with passive learning, active learning is able to reduce the label complexity exponentially if the data are linearly separable or satisfy the Tsybakov noise condition with parameter $\kappa=1$. In this paper, we propose a novel active learning algorithm using a convex surrogate loss, with the goal to broaden the cases for which active learning achieves an exponential improvement. We make use of a convex loss not only because it reduces the computational cost, but more importantly because it leads to a tight bound for the empirical process (i.e., the difference between the empirical estimation and the expectation) when the current solution is close to the optimal one. Under the assumption that the norm of the optimal classifier that minimizes the convex risk is available, our analysis shows that the introduction of the convex surrogate loss yields an exponential reduction in the label complexity even when the parameter $\kappa$ of the Tsybakov noise is larger than $1$. To the best of our knowledge, this is the first work that improves the minimax rate of active learning by utilizing certain priori knowledge.

MixedGrad: An O Convergence Rate Algorithm for Stochastic Smooth Optimization

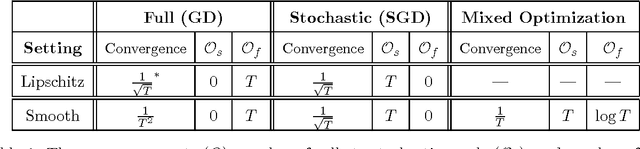
It is well known that the optimal convergence rate for stochastic optimization of smooth functions is $O(1/\sqrt{T})$, which is same as stochastic optimization of Lipschitz continuous convex functions. This is in contrast to optimizing smooth functions using full gradients, which yields a convergence rate of $O(1/T^2)$. In this work, we consider a new setup for optimizing smooth functions, termed as {\bf Mixed Optimization}, which allows to access both a stochastic oracle and a full gradient oracle. Our goal is to significantly improve the convergence rate of stochastic optimization of smooth functions by having an additional small number of accesses to the full gradient oracle. We show that, with an $O(\ln T)$ calls to the full gradient oracle and an $O(T)$ calls to the stochastic oracle, the proposed mixed optimization algorithm is able to achieve an optimization error of $O(1/T)$.

An Efficient Primal-Dual Prox Method for Non-Smooth Optimization

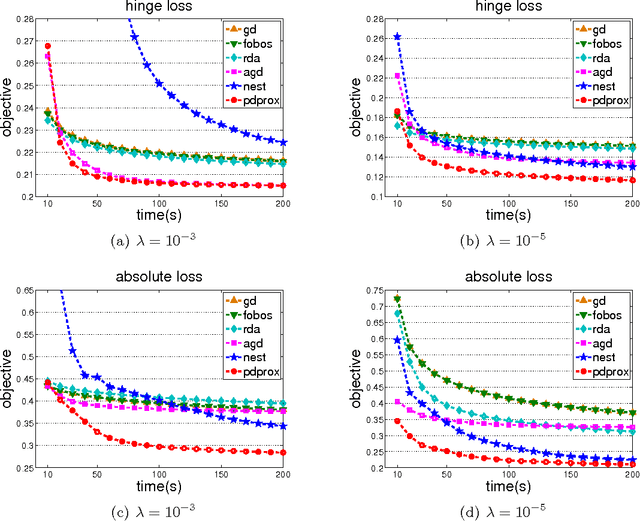
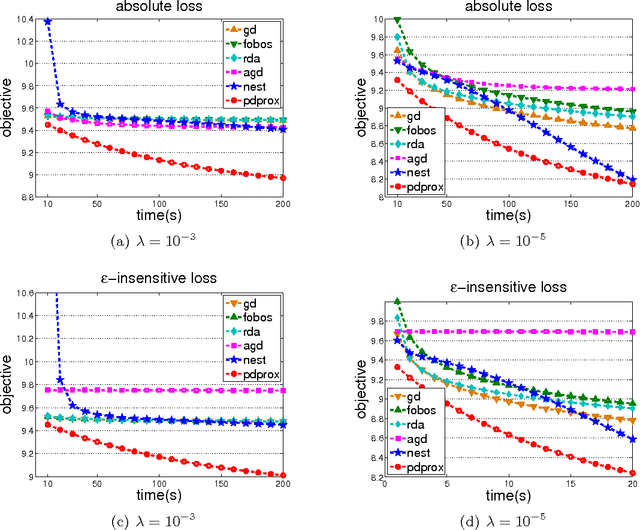
We study the non-smooth optimization problems in machine learning, where both the loss function and the regularizer are non-smooth functions. Previous studies on efficient empirical loss minimization assume either a smooth loss function or a strongly convex regularizer, making them unsuitable for non-smooth optimization. We develop a simple yet efficient method for a family of non-smooth optimization problems where the dual form of the loss function is bilinear in primal and dual variables. We cast a non-smooth optimization problem into a minimax optimization problem, and develop a primal dual prox method that solves the minimax optimization problem at a rate of $O(1/T)$ {assuming that the proximal step can be efficiently solved}, significantly faster than a standard subgradient descent method that has an $O(1/\sqrt{T})$ convergence rate. Our empirical study verifies the efficiency of the proposed method for various non-smooth optimization problems that arise ubiquitously in machine learning by comparing it to the state-of-the-art first order methods.

Online Stochastic Optimization with Multiple Objectives

In this paper we propose a general framework to characterize and solve the stochastic optimization problems with multiple objectives underlying many real world learning applications. We first propose a projection based algorithm which attains an $O(T^{-1/3})$ convergence rate. Then, by leveraging on the theory of Lagrangian in constrained optimization, we devise a novel primal-dual stochastic approximation algorithm which attains the optimal convergence rate of $O(T^{-1/2})$ for general Lipschitz continuous objectives.

Passive Learning with Target Risk

In this paper we consider learning in passive setting but with a slight modification. We assume that the target expected loss, also referred to as target risk, is provided in advance for learner as prior knowledge. Unlike most studies in the learning theory that only incorporate the prior knowledge into the generalization bounds, we are able to explicitly utilize the target risk in the learning process. Our analysis reveals a surprising result on the sample complexity of learning: by exploiting the target risk in the learning algorithm, we show that when the loss function is both strongly convex and smooth, the sample complexity reduces to $\O(\log (\frac{1}{\epsilon}))$, an exponential improvement compared to the sample complexity $\O(\frac{1}{\epsilon})$ for learning with strongly convex loss functions. Furthermore, our proof is constructive and is based on a computationally efficient stochastic optimization algorithm for such settings which demonstrate that the proposed algorithm is practically useful.

Sparse Multiple Kernel Learning with Geometric Convergence Rate

In this paper, we study the problem of sparse multiple kernel learning (MKL), where the goal is to efficiently learn a combination of a fixed small number of kernels from a large pool that could lead to a kernel classifier with a small prediction error. We develop an efficient algorithm based on the greedy coordinate descent algorithm, that is able to achieve a geometric convergence rate under appropriate conditions. The convergence rate is achieved by measuring the size of functional gradients by an empirical $\ell_2$ norm that depends on the empirical data distribution. This is in contrast to previous algorithms that use a functional norm to measure the size of gradients, which is independent from the data samples. We also establish a generalization error bound of the learned sparse kernel classifier using the technique of local Rademacher complexity.

Efficient Constrained Regret Minimization

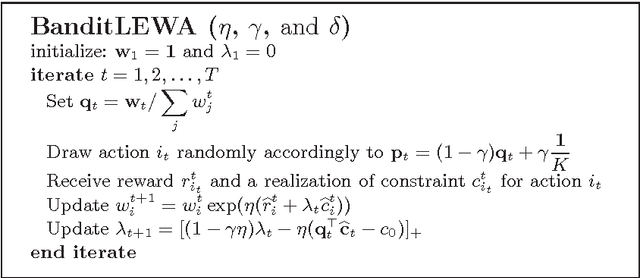
Online learning constitutes a mathematical and compelling framework to analyze sequential decision making problems in adversarial environments. The learner repeatedly chooses an action, the environment responds with an outcome, and then the learner receives a reward for the played action. The goal of the learner is to maximize his total reward. However, there are situations in which, in addition to maximizing the cumulative reward, there are some additional constraints on the sequence of decisions that must be satisfied on average by the learner. In this paper we study an extension to the online learning where the learner aims to maximize the total reward given that some additional constraints need to be satisfied. By leveraging on the theory of Lagrangian method in constrained optimization, we propose Lagrangian exponentially weighted average (LEWA) algorithm, which is a primal-dual variant of the well known exponentially weighted average algorithm, to efficiently solve constrained online decision making problems. Using novel theoretical analysis, we establish the regret and the violation of the constraint bounds in full information and bandit feedback models.

Trading Regret for Efficiency: Online Convex Optimization with Long Term Constraints

In this paper we propose a framework for solving constrained online convex optimization problem. Our motivation stems from the observation that most algorithms proposed for online convex optimization require a projection onto the convex set $\mathcal{K}$ from which the decisions are made. While for simple shapes (e.g. Euclidean ball) the projection is straightforward, for arbitrary complex sets this is the main computational challenge and may be inefficient in practice. In this paper, we consider an alternative online convex optimization problem. Instead of requiring decisions belong to $\mathcal{K}$ for all rounds, we only require that the constraints which define the set $\mathcal{K}$ be satisfied in the long run. We show that our framework can be utilized to solve a relaxed version of online learning with side constraints addressed in \cite{DBLP:conf/colt/MannorT06} and \cite{DBLP:conf/aaai/KvetonYTM08}. By turning the problem into an online convex-concave optimization problem, we propose an efficient algorithm which achieves $\tilde{\mathcal{O}}(\sqrt{T})$ regret bound and $\tilde{\mathcal{O}}(T^{3/4})$ bound for the violation of constraints. Then we modify the algorithm in order to guarantee that the constraints are satisfied in the long run. This gain is achieved at the price of getting $\tilde{\mathcal{O}}(T^{3/4})$ regret bound. Our second algorithm is based on the Mirror Prox method \citep{nemirovski-2005-prox} to solve variational inequalities which achieves $\tilde{\mathcal{\mathcal{O}}}(T^{2/3})$ bound for both regret and the violation of constraints when the domain $\K$ can be described by a finite number of linear constraints. Finally, we extend the result to the setting where we only have partial access to the convex set $\mathcal{K}$ and propose a multipoint bandit feedback algorithm with the same bounds in expectation as our first algorithm.

An Improved Bound for the Nystrom Method for Large Eigengap

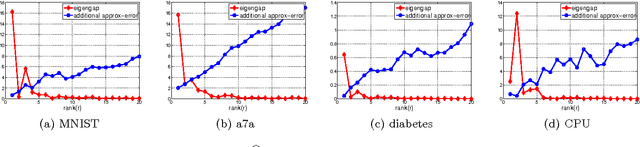
We develop an improved bound for the approximation error of the Nystr\"{o}m method under the assumption that there is a large eigengap in the spectrum of kernel matrix. This is based on the empirical observation that the eigengap has a significant impact on the approximation error of the Nystr\"{o}m method. Our approach is based on the concentration inequality of integral operator and the theory of matrix perturbation. Our analysis shows that when there is a large eigengap, we can improve the approximation error of the Nystr\"{o}m method from $O(N/m^{1/4})$ to $O(N/m^{1/2})$ when measured in Frobenius norm, where $N$ is the size of the kernel matrix, and $m$ is the number of sampled columns.