Equivalence in Deep Neural Networks via Conjugate Matrix Ensembles

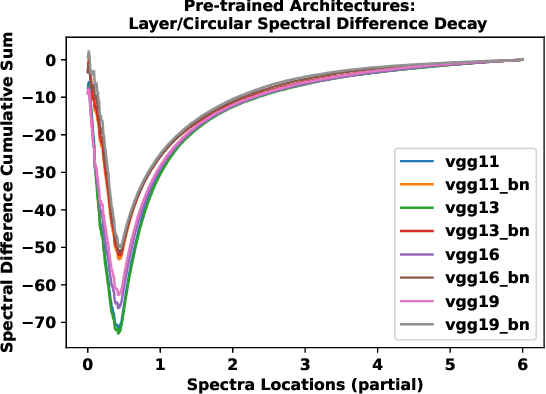
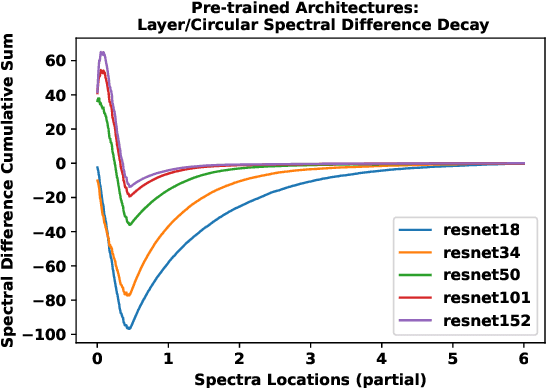
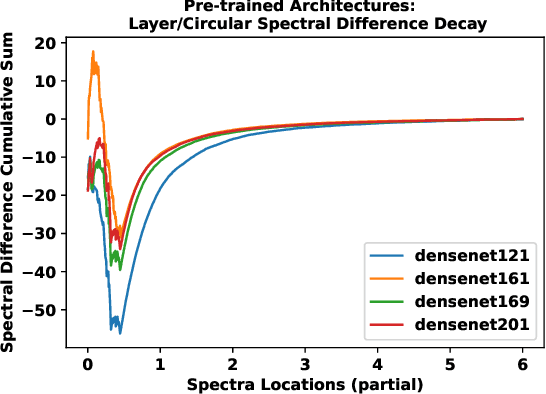
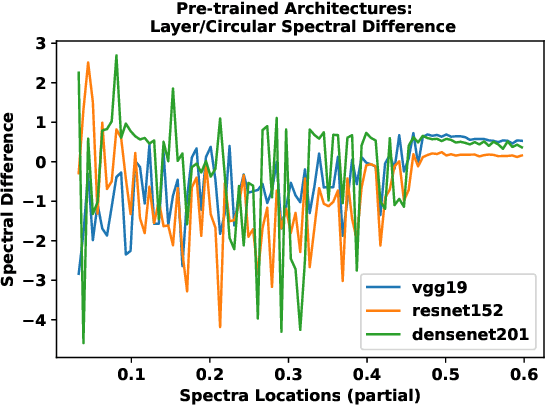
A numerical approach is developed for detecting the equivalence of deep learning architectures. The method is based on generating Mixed Matrix Ensembles (MMEs) out of deep neural network weight matrices and {\it conjugate circular ensemble} matching the neural architecture topology. Following this, the empirical evidence supports the {\it phenomenon} that distance between spectral densities of neural architectures and corresponding {\it conjugate circular ensemble} are vanishing with different decay rates at long positive tail part of the spectrum i.e., cumulative Circular Spectral Distance (CSD). This finding can be used in establishing equivalences among different neural architectures via analysis of fluctuations in CSD. We investigated this phenomenon for wide range of deep learning vision architectures and with circular ensembles originating from statistical quantum mechanics. Practical implications of the proposed method for artificial and natural neural architectures discussed such as possibility of using the approach in Neural Architecture Search (NAS) and classification of biological neural networks.

Periodic Spectral Ergodicity: A Complexity Measure for Deep Neural Networks and Neural Architecture Search

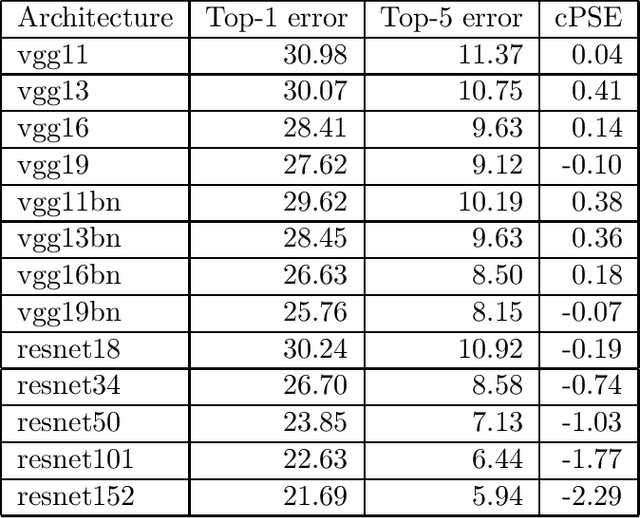
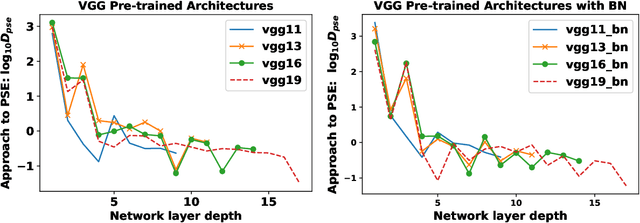
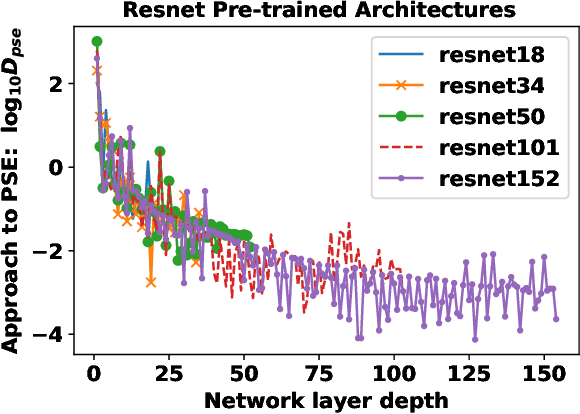
Establishing associations between the structure and the learning ability of deep neural networks (DNNs) is a challenging task in modern machine learning. Producing solutions to this challenge will bring progress both in the theoretical understanding of DNNs and in building new architectures efficiently. In this work, we address this challenge by developing a new simple complexity measure based on another new measure called Periodic Spectral Ergodicity (PSE) originating from quantum statistical mechanics. Based on this measure a framework is devised in quantifying the complexity of deep neural network from its learned weights and traversing network connectivity in a sequential manner, hence the term cascading PSE (cPSE) as an empirical complexity measure. Because of this cascading approach, i.e., a symmetric divergence of PSE on the consecutive layers, it is possible to use this measure in addition for Neural Architecture Search (NAS). We demonstrate the usefulness of this measure in practice on two sets of vision models, ResNet and VGG and sketch the computation of cPSE for more complex network structures.

Generalised learning of time-series: Ornstein-Uhlenbeck processes

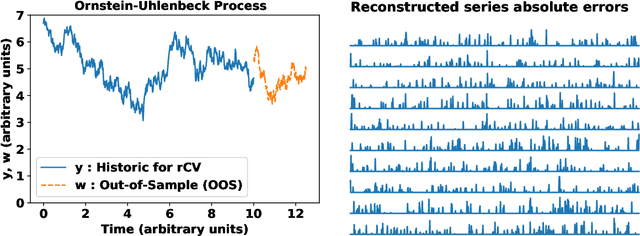
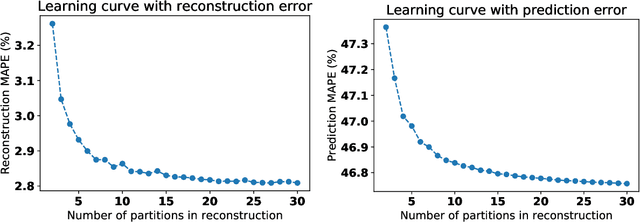
In machine learning, statistics, econometrics and statistical physics, $k$-fold cross-validation (CV) is used as a standard approach in quantifying the generalization performance of a statistical model. Applying this approach directly to time series models is avoided by practitioners due to intrinsic nature of serial correlations in the ordered data due to implications like absurdity of using future data to predict past and non-stationarity issues. In this work, we propose a technique called {\it reconstructive cross validation} ($rCV$) that avoids all these issues enabling generalized learning in time-series as a meta-algorithm. In $rCV$, data points in the test fold, randomly selected points from the time series, are first removed. Then, a secondary time series model or a technique is used in reconstructing the removed points from the test fold, i.e., imputation or smoothing. Thereafter, the primary model is build using new dataset coming from the secondary model or a technique. The performance of the primary model on the test set by computing the deviations from the originally removed and out-of-sample (OSS) data are evaluated simultaneously. This amounts to reconstruction and prediction errors. By this procedure serial correlations and data order is retained and $k$-fold cross-validation is reached generically. If reconstruction model uses a technique whereby the existing data points retained exactly, such as Gaussian process regression, the reconstruction itself will not result in information loss from non-reconstructed portion of the original data points. We have applied $rCV$ to estimate the general performance of the model build on simulated Ornstein-Uhlenbeck process. We have shown an approach to build a time-series learning curves utilizing $rCV$.

HARK Side of Deep Learning -- From Grad Student Descent to Automated Machine Learning

Recent advancements in machine learning research, i.e., deep learning, introduced methods that excel conventional algorithms as well as humans in several complex tasks, ranging from detection of objects in images and speech recognition to playing difficult strategic games. However, the current methodology of machine learning research and consequently, implementations of the real-world applications of such algorithms, seems to have a recurring HARKing (Hypothesizing After the Results are Known) issue. In this work, we elaborate on the algorithmic, economic and social reasons and consequences of this phenomenon. We present examples from current common practices of conducting machine learning research (e.g. avoidance of reporting negative results) and failure of generalization ability of the proposed algorithms and datasets in actual real-life usage. Furthermore, a potential future trajectory of machine learning research and development from the perspective of accountable, unbiased, ethical and privacy-aware algorithmic decision making is discussed. We would like to emphasize that with this discussion we neither claim to provide an exhaustive argumentation nor blame any specific institution or individual on the raised issues. This is simply a discussion put forth by us, insiders of the machine learning field, reflecting on us.

Spectral Ergodicity in Deep Learning Architectures via Surrogate Random Matrices

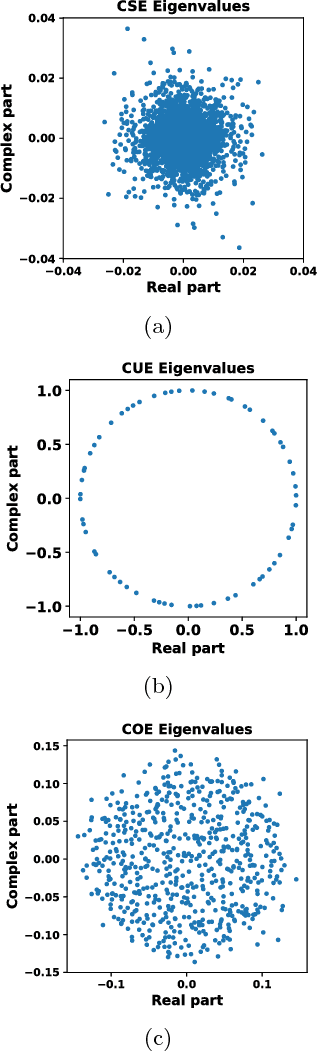
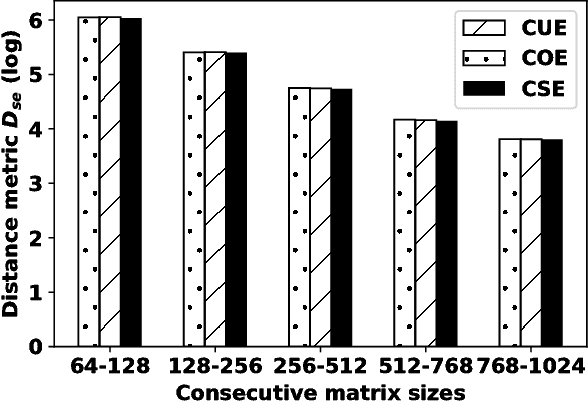
In this work a novel method to quantify spectral ergodicity for random matrices is presented. The new methodology combines approaches rooted in the metrics of Thirumalai-Mountain (TM) and Kullbach-Leibler (KL) divergence. The method is applied to a general study of deep and recurrent neural networks via the analysis of random matrix ensembles mimicking typical weight matrices of those systems. In particular, we examine circular random matrix ensembles: circular unitary ensemble (CUE), circular orthogonal ensemble (COE), and circular symplectic ensemble (CSE). Eigenvalue spectra and spectral ergodicity are computed for those ensembles as a function of network size. It is observed that as the matrix size increases the level of spectral ergodicity of the ensemble rises, i.e., the eigenvalue spectra obtained for a single realisation at random from the ensemble is closer to the spectra obtained averaging over the whole ensemble. Based on previous results we conjecture that success of deep learning architectures is strongly bound to the concept of spectral ergodicity. The method to compute spectral ergodicity proposed in this work could be used to optimise the size and architecture of deep as well as recurrent neural networks.