Embedded Nonlocal Operator Regression (ENOR): Quantifying model error in learning nonlocal operators

Nonlocal, integral operators have become an efficient surrogate for bottom-up homogenization, due to their ability to represent long-range dependence and multiscale effects. However, the nonlocal homogenized model has unavoidable discrepancy from the microscale model. Such errors accumulate and propagate in long-term simulations, making the resultant prediction unreliable. To develop a robust and reliable bottom-up homogenization framework, we propose a new framework, which we coin Embedded Nonlocal Operator Regression (ENOR), to learn a nonlocal homogenized surrogate model and its structural model error. This framework provides discrepancy-adaptive uncertainty quantification for homogenized material response predictions in long-term simulations. The method is built on Nonlocal Operator Regression (NOR), an optimization-based nonlocal kernel learning approach, together with an embedded model error term in the trainable kernel. Then, Bayesian inference is employed to infer the model error term parameters together with the kernel parameters. To make the problem computationally feasible, we use a multilevel delayed acceptance Markov chain Monte Carlo (MLDA-MCMC) method, enabling efficient Bayesian model calibration and model error estimation. We apply this technique to predict long-term wave propagation in a heterogeneous one-dimensional bar, and compare its performance with additive noise models. Owing to its ability to capture model error, the learned ENOR achieves improved estimation of posterior predictive uncertainty.

ML-based identification of the interface regions for coupling local and nonlocal models

Local-nonlocal coupling approaches combine the computational efficiency of local models and the accuracy of nonlocal models. However, the coupling process is challenging, requiring expertise to identify the interface between local and nonlocal regions. This study introduces a machine learning-based approach to automatically detect the regions in which the local and nonlocal models should be used in a coupling approach. This identification process uses the loading functions and provides as output the selected model at the grid points. Training is based on datasets of loading functions for which reference coupling configurations are computed using accurate coupled solutions, where accuracy is measured in terms of the relative error between the solution to the coupling approach and the solution to the nonlocal model. We study two approaches that differ from one another in terms of the data structure. The first approach, referred to as the full-domain input data approach, inputs the full load vector and outputs a full label vector. In this case, the classification process is carried out globally. The second approach consists of a window-based approach, where loads are preprocessed and partitioned into windows and the problem is formulated as a node-wise classification approach in which the central point of each window is treated individually. The classification problems are solved via deep learning algorithms based on convolutional neural networks. The performance of these approaches is studied on one-dimensional numerical examples using F1-scores and accuracy metrics. In particular, it is shown that the windowing approach provides promising results, achieving an accuracy of 0.96 and an F1-score of 0.97. These results underscore the potential of the approach to automate coupling processes, leading to more accurate and computationally efficient solutions for material science applications.

GNN-based physics solver for time-independent PDEs

Physics-based deep learning frameworks have shown to be effective in accurately modeling the dynamics of complex physical systems with generalization capability across problem inputs. However, time-independent problems pose the challenge of requiring long-range exchange of information across the computational domain for obtaining accurate predictions. In the context of graph neural networks (GNNs), this calls for deeper networks, which, in turn, may compromise or slow down the training process. In this work, we present two GNN architectures to overcome this challenge - the Edge Augmented GNN and the Multi-GNN. We show that both these networks perform significantly better (by a factor of 1.5 to 2) than baseline methods when applied to time-independent solid mechanics problems. Furthermore, the proposed architectures generalize well to unseen domains, boundary conditions, and materials. Here, the treatment of variable domains is facilitated by a novel coordinate transformation that enables rotation and translation invariance. By broadening the range of problems that neural operators based on graph neural networks can tackle, this paper provides the groundwork for their application to complex scientific and industrial settings.

Towards a unified nonlocal, peridynamics framework for the coarse-graining of molecular dynamics data with fractures

Molecular dynamics (MD) has served as a powerful tool for designing materials with reduced reliance on laboratory testing. However, the use of MD directly to treat the deformation and failure of materials at the mesoscale is still largely beyond reach. Herein, we propose a learning framework to extract a peridynamic model as a mesoscale continuum surrogate from MD simulated material fracture datasets. Firstly, we develop a novel coarse-graining method, to automatically handle the material fracture and its corresponding discontinuities in MD displacement dataset. Inspired by the Weighted Essentially Non-Oscillatory scheme, the key idea lies at an adaptive procedure to automatically choose the locally smoothest stencil, then reconstruct the coarse-grained material displacement field as piecewise smooth solutions containing discontinuities. Then, based on the coarse-grained MD data, a two-phase optimization-based learning approach is proposed to infer the optimal peridynamics model with damage criterion. In the first phase, we identify the optimal nonlocal kernel function from datasets without material damage, to capture the material stiffness properties. Then, in the second phase, the material damage criterion is learnt as a smoothed step function from the data with fractures. As a result, a peridynamics surrogate is obtained. Our peridynamics surrogate model can be employed in further prediction tasks with different grid resolutions from training, and hence allows for substantial reductions in computational cost compared with MD. We illustrate the efficacy of the proposed approach with several numerical tests for single layer graphene. Our tests show that the proposed data-driven model is robust and generalizable: it is capable in modeling the initialization and growth of fractures under discretization and loading settings that are different from the ones used during training.

Probabilistic partition of unity networks for high-dimensional regression problems

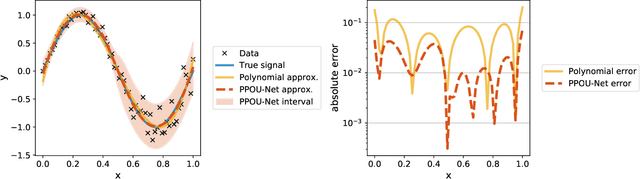
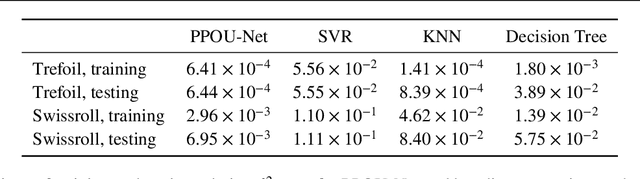
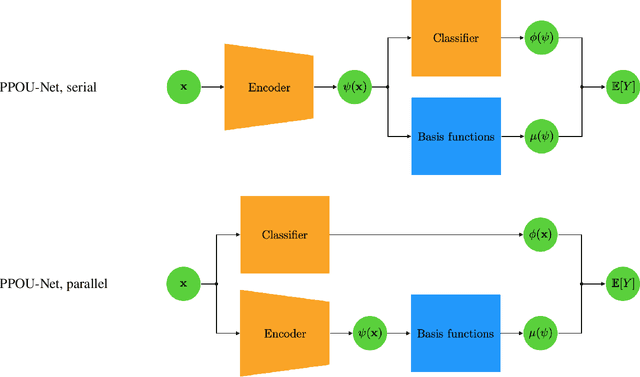
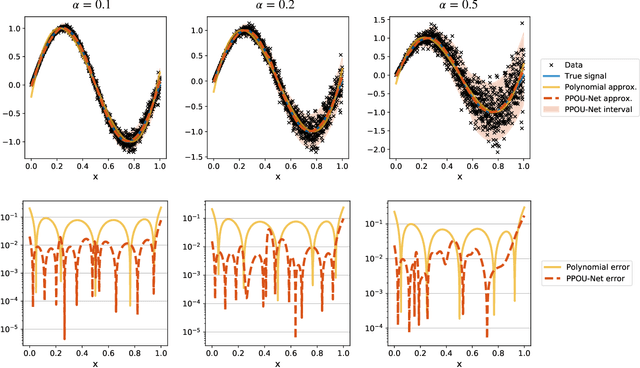
We explore the probabilistic partition of unity network (PPOU-Net) model in the context of high-dimensional regression problems. With the PPOU-Nets, the target function for any given input is approximated by a mixture of experts model, where each cluster is associated with a fixed-degree polynomial. The weights of the clusters are determined by a DNN that defines a partition of unity. The weighted average of the polynomials approximates the target function and produces uncertainty quantification naturally. Our training strategy leverages automatic differentiation and the expectation maximization (EM) algorithm. During the training, we (i) apply gradient descent to update the DNN coefficients; (ii) update the polynomial coefficients using weighted least-squares solves; and (iii) compute the variance of each cluster according to a closed-form formula derived from the EM algorithm. The PPOU-Nets consistently outperform the baseline fully-connected neural networks of comparable sizes in numerical experiments of various data dimensions. We also explore the proposed model in applications of quantum computing, where the PPOU-Nets act as surrogate models for cost landscapes associated with variational quantum circuits.

Machine Learning in Heterogeneous Porous Materials

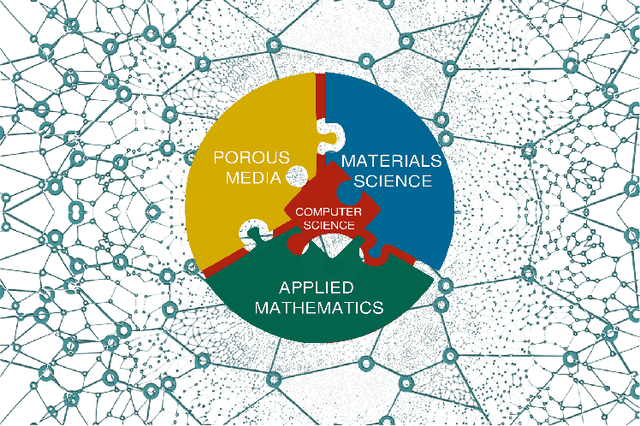
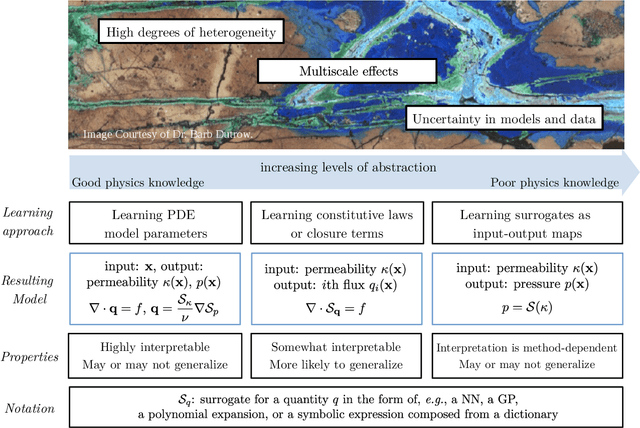
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

Nonlocal Kernel Network (NKN): a Stable and Resolution-Independent Deep Neural Network

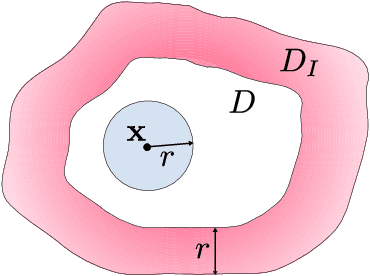
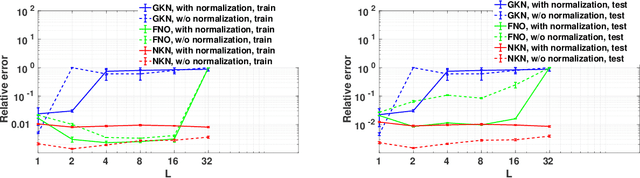
Neural operators have recently become popular tools for designing solution maps between function spaces in the form of neural networks. Differently from classical scientific machine learning approaches that learn parameters of a known partial differential equation (PDE) for a single instance of the input parameters at a fixed resolution, neural operators approximate the solution map of a family of PDEs. Despite their success, the uses of neural operators are so far restricted to relatively shallow neural networks and confined to learning hidden governing laws. In this work, we propose a novel nonlocal neural operator, which we refer to as nonlocal kernel network (NKN), that is resolution independent, characterized by deep neural networks, and capable of handling a variety of tasks such as learning governing equations and classifying images. Our NKN stems from the interpretation of the neural network as a discrete nonlocal diffusion reaction equation that, in the limit of infinite layers, is equivalent to a parabolic nonlocal equation, whose stability is analyzed via nonlocal vector calculus. The resemblance with integral forms of neural operators allows NKNs to capture long-range dependencies in the feature space, while the continuous treatment of node-to-node interactions makes NKNs resolution independent. The resemblance with neural ODEs, reinterpreted in a nonlocal sense, and the stable network dynamics between layers allow for generalization of NKN's optimal parameters from shallow to deep networks. This fact enables the use of shallow-to-deep initialization techniques. Our tests show that NKNs outperform baseline methods in both learning governing equations and image classification tasks and generalize well to different resolutions and depths.

A data-driven peridynamic continuum model for upscaling molecular dynamics

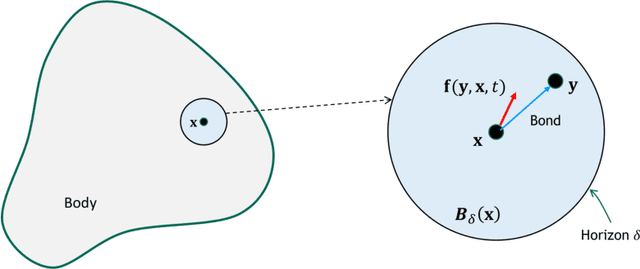
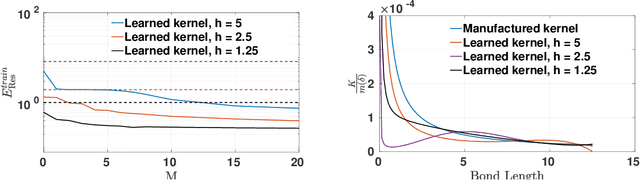
Nonlocal models, including peridynamics, often use integral operators that embed lengthscales in their definition. However, the integrands in these operators are difficult to define from the data that are typically available for a given physical system, such as laboratory mechanical property tests. In contrast, molecular dynamics (MD) does not require these integrands, but it suffers from computational limitations in the length and time scales it can address. To combine the strengths of both methods and to obtain a coarse-grained, homogenized continuum model that efficiently and accurately captures materials' behavior, we propose a learning framework to extract, from MD data, an optimal Linear Peridynamic Solid (LPS) model as a surrogate for MD displacements. To maximize the accuracy of the learnt model we allow the peridynamic influence function to be partially negative, while preserving the well-posedness of the resulting model. To achieve this, we provide sufficient well-posedness conditions for discretized LPS models with sign-changing influence functions and develop a constrained optimization algorithm that minimizes the equation residual while enforcing such solvability conditions. This framework guarantees that the resulting model is mathematically well-posed, physically consistent, and that it generalizes well to settings that are different from the ones used during training. We illustrate the efficacy of the proposed approach with several numerical tests for single layer graphene. Our two-dimensional tests show the robustness of the proposed algorithm on validation data sets that include thermal noise, different domain shapes and external loadings, and discretizations substantially different from the ones used for training.

Data-driven learning of nonlocal models: from high-fidelity simulations to constitutive laws

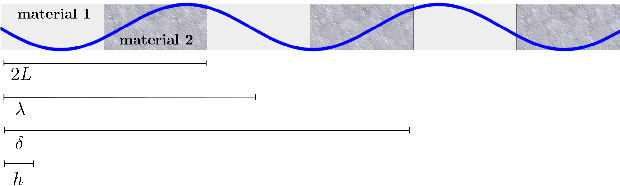
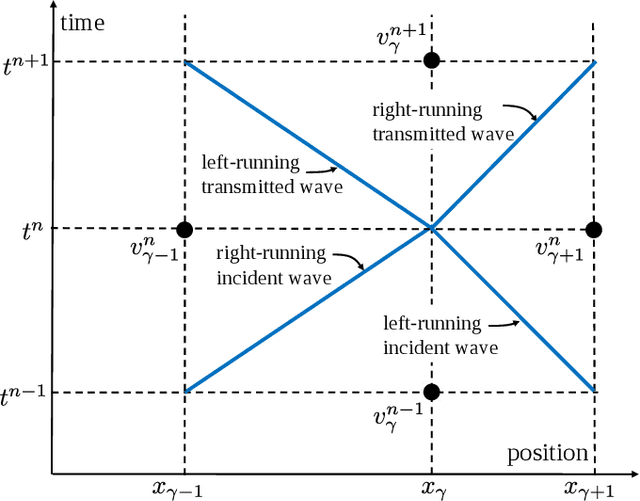
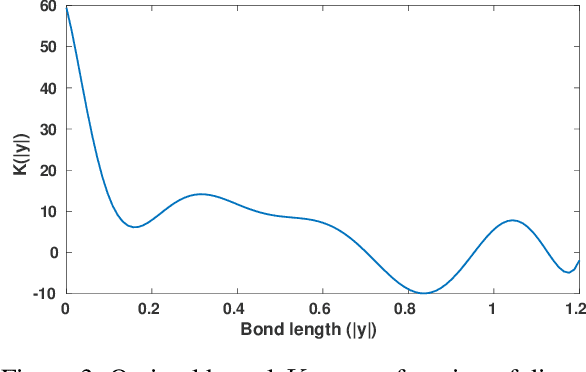
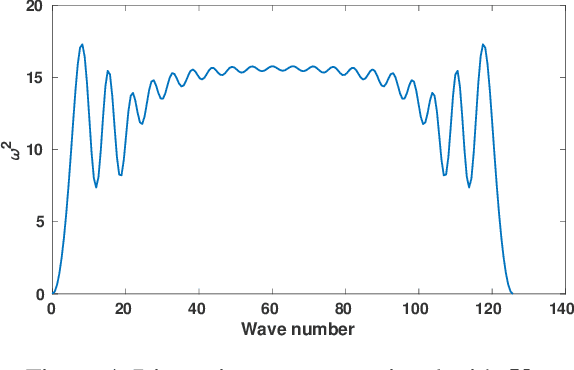
We show that machine learning can improve the accuracy of simulations of stress waves in one-dimensional composite materials. We propose a data-driven technique to learn nonlocal constitutive laws for stress wave propagation models. The method is an optimization-based technique in which the nonlocal kernel function is approximated via Bernstein polynomials. The kernel, including both its functional form and parameters, is derived so that when used in a nonlocal solver, it generates solutions that closely match high-fidelity data. The optimal kernel therefore acts as a homogenized nonlocal continuum model that accurately reproduces wave motion in a smaller-scale, more detailed model that can include multiple materials. We apply this technique to wave propagation within a heterogeneous bar with a periodic microstructure. Several one-dimensional numerical tests illustrate the accuracy of our algorithm. The optimal kernel is demonstrated to reproduce high-fidelity data for a composite material in applications that are substantially different from the problems used as training data.

Data-driven learning of robust nonlocal physics from high-fidelity synthetic data

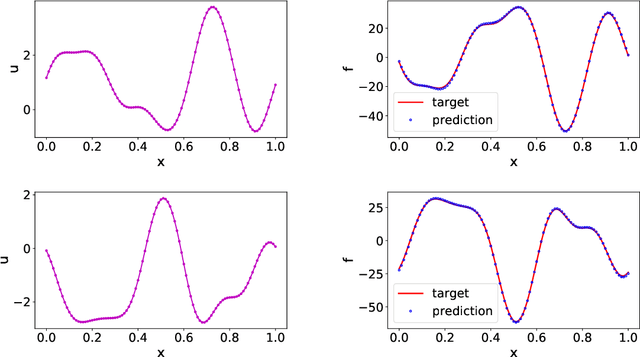
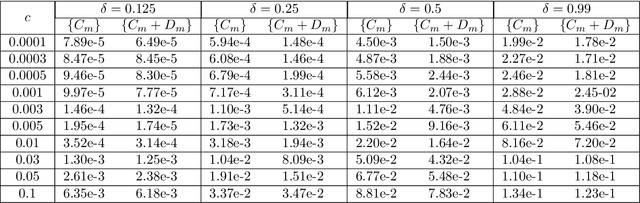
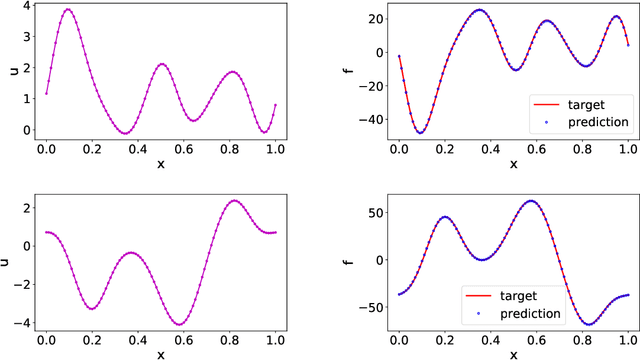
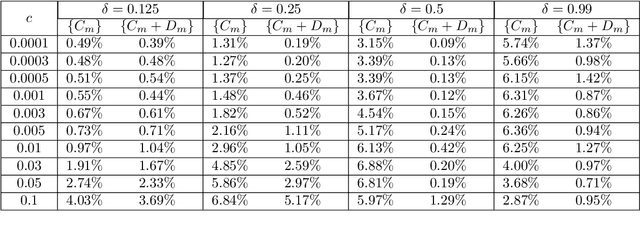
A key challenge to nonlocal models is the analytical complexity of deriving them from first principles, and frequently their use is justified a posteriori. In this work we extract nonlocal models from data, circumventing these challenges and providing data-driven justification for the resulting model form. Extracting provably robust data-driven surrogates is a major challenge for machine learning (ML) approaches, due to nonlinearities and lack of convexity. Our scheme allows extraction of provably invertible nonlocal models whose kernels may be partially negative. To achieve this, based on established nonlocal theory, we embed in our algorithm sufficient conditions on the non-positive part of the kernel that guarantee well-posedness of the learnt operator. These conditions are imposed as inequality constraints and ensure that models are robust, even in small-data regimes. We demonstrate this workflow for a range of applications, including reproduction of manufactured nonlocal kernels; numerical homogenization of Darcy flow associated with a heterogeneous periodic microstructure; nonlocal approximation to high-order local transport phenomena; and approximation of globally supported fractional diffusion operators by truncated kernels.