FP-IRL: Fokker-Planck-based Inverse Reinforcement Learning -- A Physics-Constrained Approach to Markov Decision Processes

Inverse Reinforcement Learning (IRL) is a compelling technique for revealing the rationale underlying the behavior of autonomous agents. IRL seeks to estimate the unknown reward function of a Markov decision process (MDP) from observed agent trajectories. However, IRL needs a transition function, and most algorithms assume it is known or can be estimated in advance from data. It therefore becomes even more challenging when such transition dynamics is not known a-priori, since it enters the estimation of the policy in addition to determining the system's evolution. When the dynamics of these agents in the state-action space is described by stochastic differential equations (SDE) in It^{o} calculus, these transitions can be inferred from the mean-field theory described by the Fokker-Planck (FP) equation. We conjecture there exists an isomorphism between the time-discrete FP and MDP that extends beyond the minimization of free energy (in FP) and maximization of the reward (in MDP). We identify specific manifestations of this isomorphism and use them to create a novel physics-aware IRL algorithm, FP-IRL, which can simultaneously infer the transition and reward functions using only observed trajectories. We employ variational system identification to infer the potential function in FP, which consequently allows the evaluation of reward, transition, and policy by leveraging the conjecture. We demonstrate the effectiveness of FP-IRL by applying it to a synthetic benchmark and a biological problem of cancer cell dynamics, where the transition function is inaccessible.

Machine Learning in Heterogeneous Porous Materials

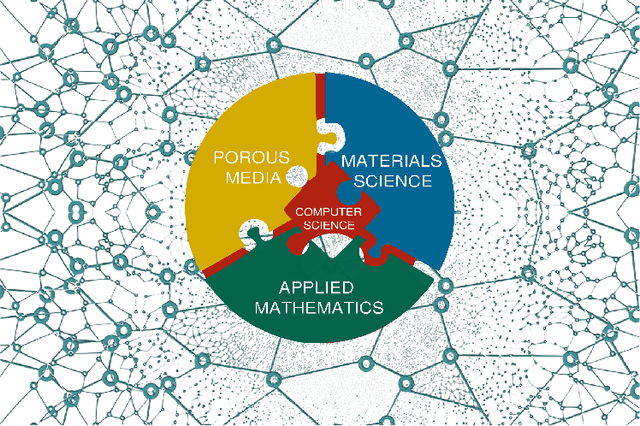
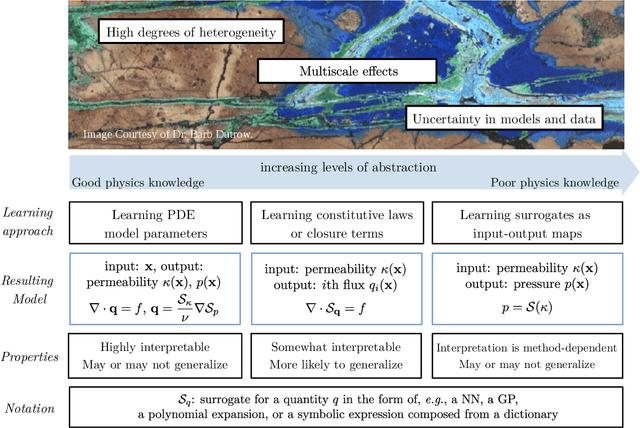
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

A heteroencoder architecture for prediction of failure locations in porous metals using variational inference

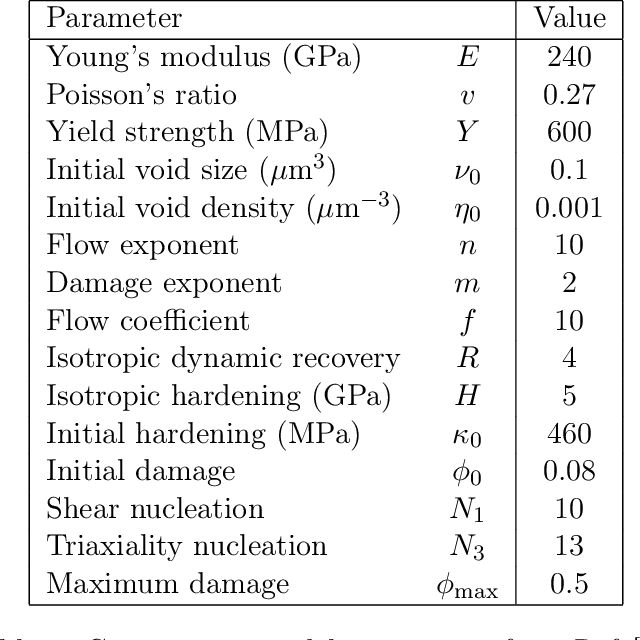
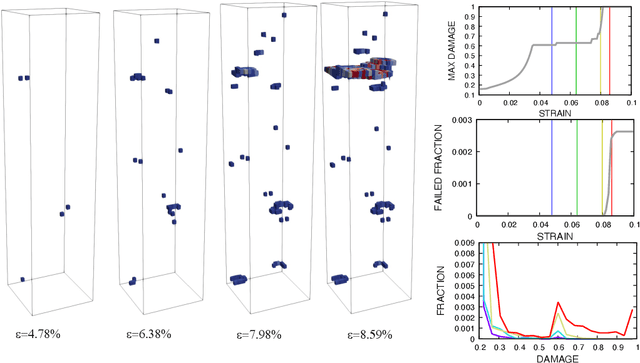
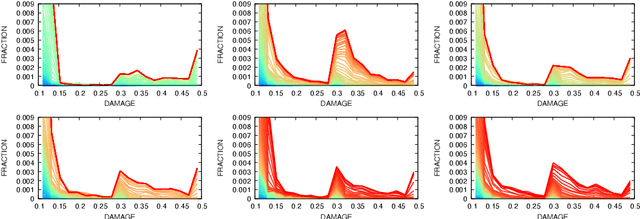
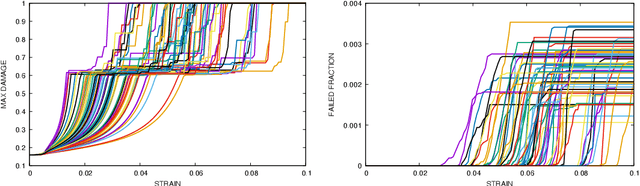
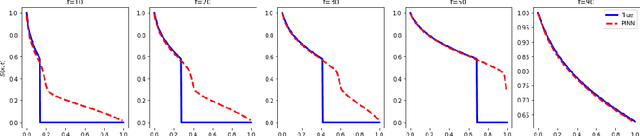
In this work we employ an encoder-decoder convolutional neural network to predict the failure locations of porous metal tension specimens based only on their initial porosities. The process we model is complex, with a progression from initial void nucleation, to saturation, and ultimately failure. The objective of predicting failure locations presents an extreme case of class imbalance since most of the material in the specimens do not fail. In response to this challenge, we develop and demonstrate the effectiveness of data- and loss-based regularization methods. Since there is considerable sensitivity of the failure location to the particular configuration of voids, we also use variational inference to provide uncertainties for the neural network predictions. We connect the deterministic and Bayesian convolutional neural networks at a theoretical level to explain how variational inference regularizes the training and predictions. We demonstrate that the resulting predicted variances are effective in ranking the locations that are most likely to fail in any given specimen.

Li$_x$CoO$_2$ phase stability studied by machine learning-enabled scale bridging between electronic structure, statistical mechanics and phase field theories

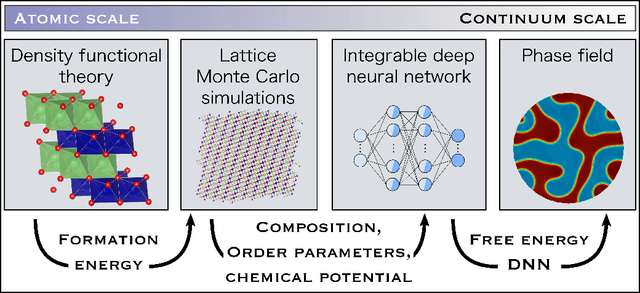
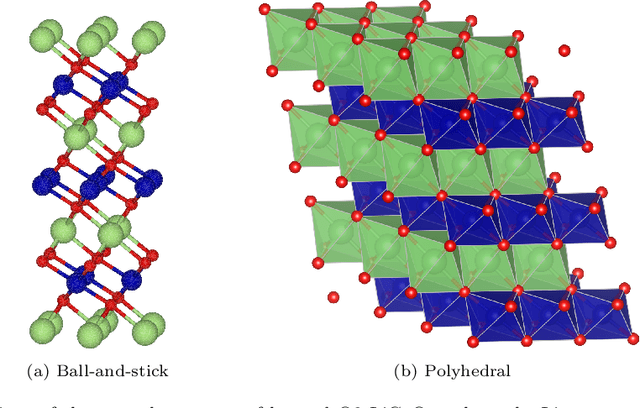
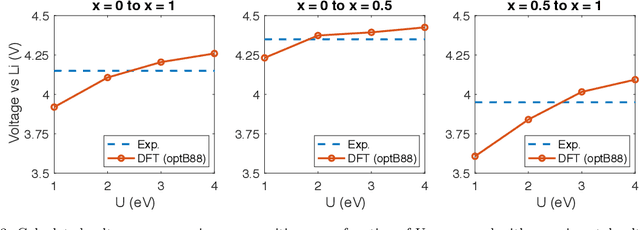
Li$_xTM$O$_2$ (TM={Ni, Co, Mn}) are promising cathodes for Li-ion batteries, whose electrochemical cycling performance is strongly governed by crystal structure and phase stability as a function of Li content at the atomistic scale. Here, we use Li$_x$CoO$_2$ (LCO) as a model system to benchmark a scale-bridging framework that combines density functional theory (DFT) calculations at the atomistic scale with phase field modeling at the continuum scale to understand the impact of phase stability on microstructure evolution. This scale bridging is accomplished by incorporating traditional statistical mechanics methods with integrable deep neural networks, which allows formation energies for specific atomic configurations to be coarse-grained and incorporated in a neural network description of the free energy of the material. The resulting realistic free energy functions enable atomistically informed phase-field simulations. These computational results allow us to make connections to experimental work on LCO cathode degradation as a function of temperature, morphology and particle size.

Bayesian neural networks for weak solution of PDEs with uncertainty quantification

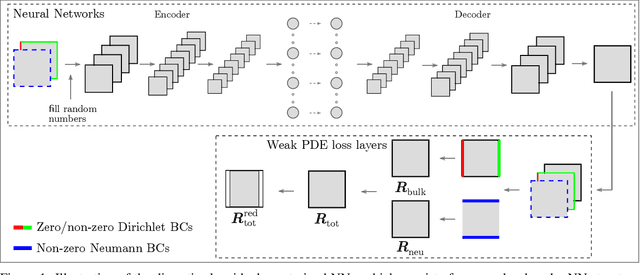
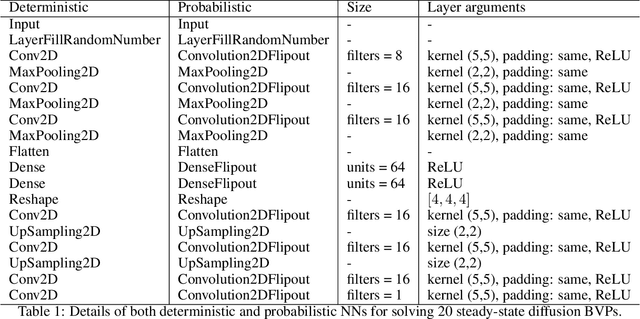
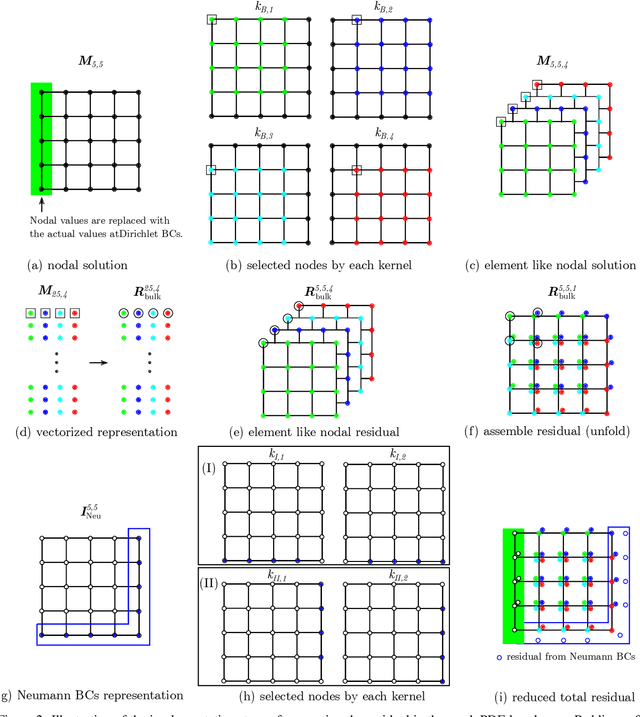
Solving partial differential equations (PDEs) is the canonical approach for understanding the behavior of physical systems. However, large scale solutions of PDEs using state of the art discretization techniques remains an expensive proposition. In this work, a new physics-constrained neural network (NN) approach is proposed to solve PDEs without labels, with a view to enabling high-throughput solutions in support of design and decision-making. Distinct from existing physics-informed NN approaches, where the strong form or weak form of PDEs are used to construct the loss function, we write the loss function of NNs based on the discretized residual of PDEs through an efficient, convolutional operator-based, and vectorized implementation. We explore an encoder-decoder NN structure for both deterministic and probabilistic models, with Bayesian NNs (BNNs) for the latter, which allow us to quantify both epistemic uncertainty from model parameters and aleatoric uncertainty from noise in the data. For BNNs, the discretized residual is used to construct the likelihood function. In our approach, both deterministic and probabilistic convolutional layers are used to learn the applied boundary conditions (BCs) and to detect the problem domain. As both Dirichlet and Neumann BCs are specified as inputs to NNs, a single NN can solve for similar physics, but with different BCs and on a number of problem domains. The trained surrogate PDE solvers can also make interpolating and extrapolating (to a certain extent) predictions for BCs that they were not exposed to during training. Such surrogate models are of particular importance for problems, where similar types of PDEs need to be repeatedly solved for many times with slight variations. We demonstrate the capability and performance of the proposed framework by applying it to steady-state diffusion, linear elasticity, and nonlinear elasticity.

Active learning workflows and integrable deep neural networks for representing the free energy functions of alloy

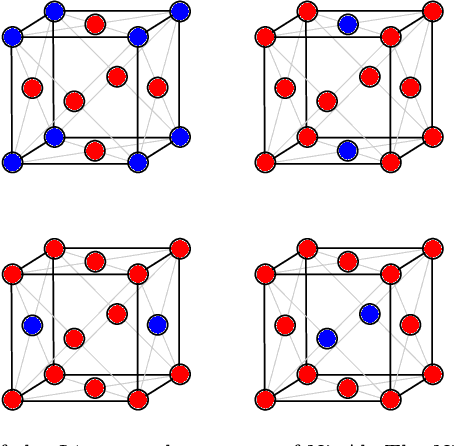
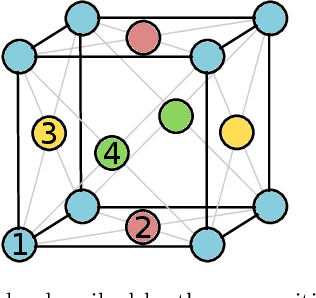
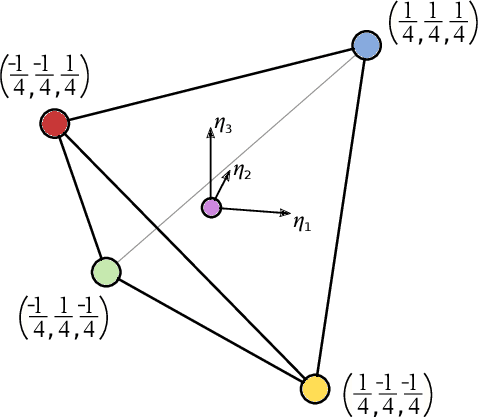
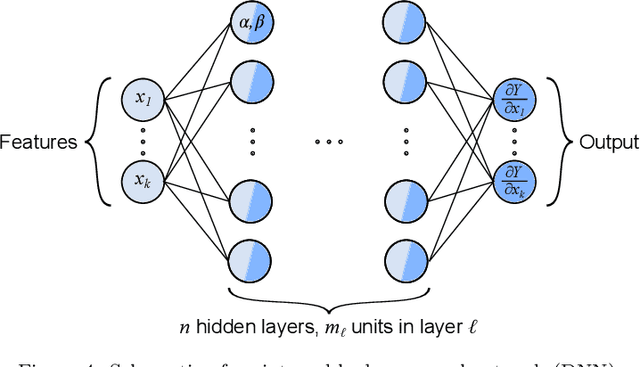
The free energy plays a fundamental role in descriptions of many systems in continuum physics. Notably, in multiphysics applications, it encodes thermodynamic coupling between different fields, such as mechanics and chemistry. It thereby gives rise to driving forces on the dynamics of interaction between the constituent phenomena. In mechano-chemically interacting materials systems, even consideration of only compositions, order parameters and strains can render the free energy to be reasonably high-dimensional. In proposing free energy functions as a paradigm for scale bridging, we have previously exploited neural networks for their representation of such high-dimensional functions. Specifically, we have developed an integrable deep neural network (IDNN) that can be trained to free energy derivative data obtained from atomic scale models and statistical mechanics, then analytically integrated to recover a free energy function. The motivation comes from the statistical mechanics formalism, in which certain free energy derivatives are accessible for control of the system, rather than the free energy itself in its entirety. Our current work combines the IDNN with an active learning workflow to improve sampling of the free energy derivative data in a high-dimensional input space. Treated as input-output maps, machine learning representations accommodate role reversals between independent and dependent quantities as the mathematical descriptions change across scale boundaries. As a prototypical material system we focus on Ni-Al. Phase field simulations using the resulting IDNN representation for the free energy of Ni-Al demonstrates that the appropriate physics of the material have been learned.