Bayesian neural networks for predicting uncertainty in full-field material response

Stress and material deformation field predictions are among the most important tasks in computational mechanics. These predictions are typically made by solving the governing equations of continuum mechanics using finite element analysis, which can become computationally prohibitive considering complex microstructures and material behaviors. Machine learning (ML) methods offer potentially cost effective surrogates for these applications. However, existing ML surrogates are either limited to low-dimensional problems and/or do not provide uncertainty estimates in the predictions. This work proposes an ML surrogate framework for stress field prediction and uncertainty quantification for diverse materials microstructures. A modified Bayesian U-net architecture is employed to provide a data-driven image-to-image mapping from initial microstructure to stress field with prediction (epistemic) uncertainty estimates. The Bayesian posterior distributions for the U-net parameters are estimated using three state-of-the-art inference algorithms: the posterior sampling-based Hamiltonian Monte Carlo method and two variational approaches, the Monte-Carlo Dropout method and the Bayes by Backprop algorithm. A systematic comparison of the predictive accuracy and uncertainty estimates for these methods is performed for a fiber reinforced composite material and polycrystalline microstructure application. It is shown that the proposed methods yield predictions of high accuracy compared to the FEA solution, while uncertainty estimates depend on the inference approach. Generally, the Hamiltonian Monte Carlo and Bayes by Backprop methods provide consistent uncertainty estimates. Uncertainty estimates from Monte Carlo Dropout, on the other hand, are more difficult to interpret and depend strongly on the method's design.

Machine Learning in Heterogeneous Porous Materials

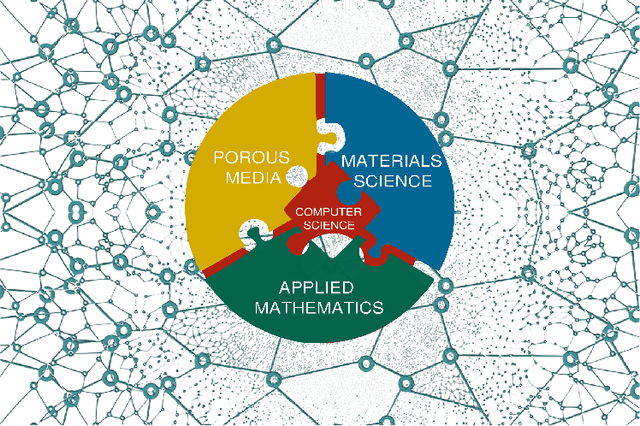
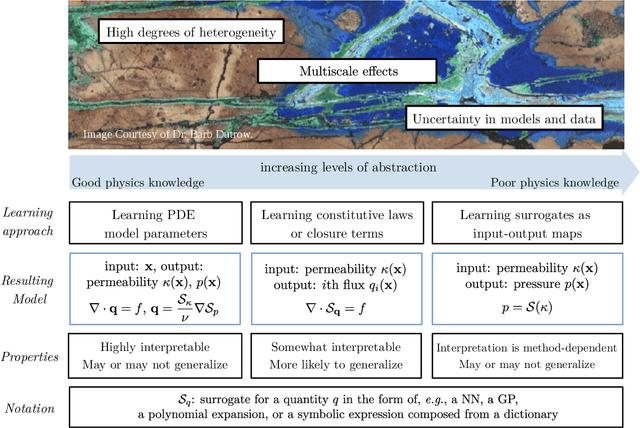
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

Stress field prediction in fiber-reinforced composite materials using a deep learning approach

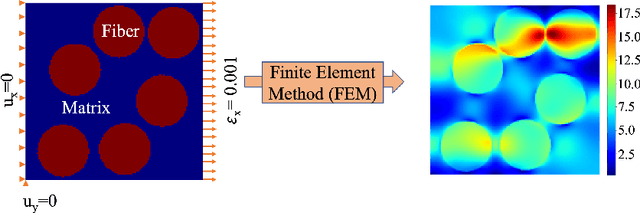
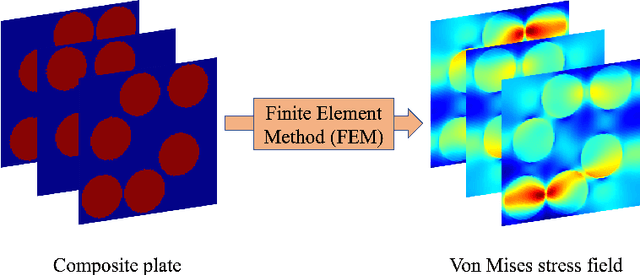
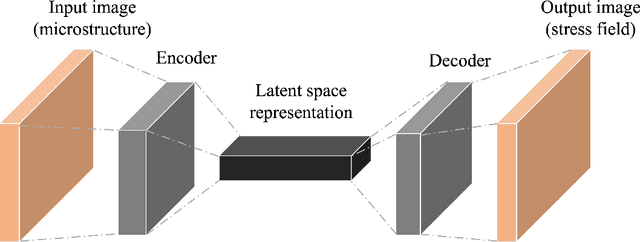
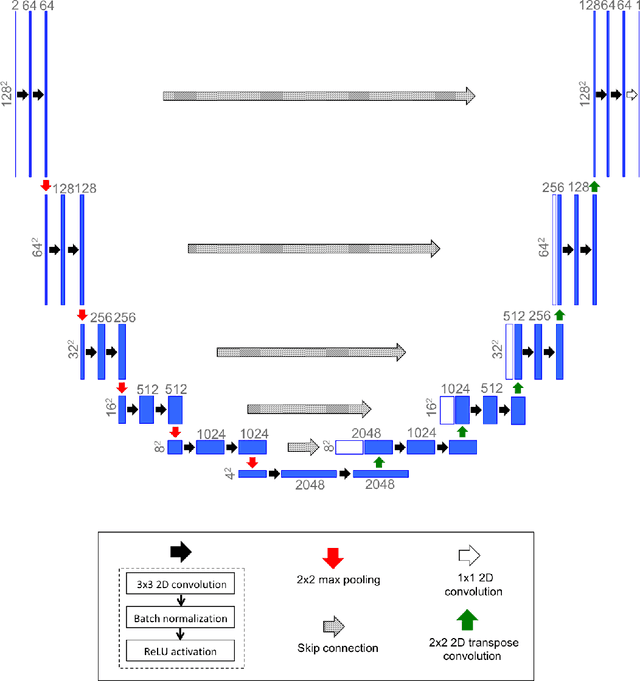
Computational stress analysis is an important step in the design of material systems. Finite element method (FEM) is a standard approach of performing stress analysis of complex material systems. A way to accelerate stress analysis is to replace FEM with a data-driven machine learning based stress analysis approach. In this study, we consider a fiber-reinforced matrix composite material system and we use deep learning tools to find an alternative to the FEM approach for stress field prediction. We first try to predict stress field maps for composite material systems of fixed number of fibers with varying spatial configurations. Specifically, we try to find a mapping between the spatial arrangement of the fibers in the composite material and the corresponding von Mises stress field. This is achieved by using a convolutional neural network (CNN), specifically a U-Net architecture, using true stress maps of systems with same number of fibers as training data. U-Net is a encoder-decoder network which in this study takes in the composite material image as an input and outputs the stress field image which is of the same size as the input image. We perform a robustness analysis by taking different initializations of the training samples to find the sensitivity of the prediction accuracy to the small number of training samples. When the number of fibers in the composite material system is increased for the same volume fraction, a finer finite element mesh discretization is required to represent the geometry accurately. This leads to an increase in the computational cost. Thus, the secondary goal here is to predict the stress field for systems with larger number of fibers with varying spatial configurations using information from the true stress maps of relatively cheaper systems of smaller fiber number.

An efficient optimization based microstructure reconstruction approach with multiple loss functions

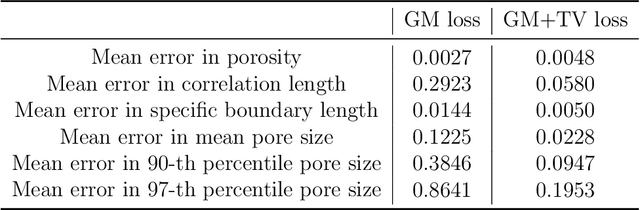
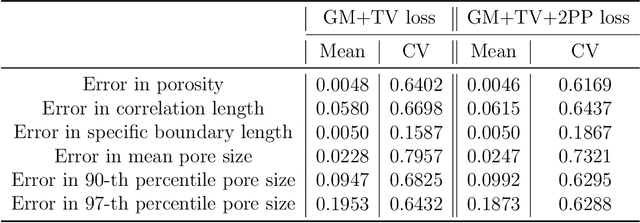
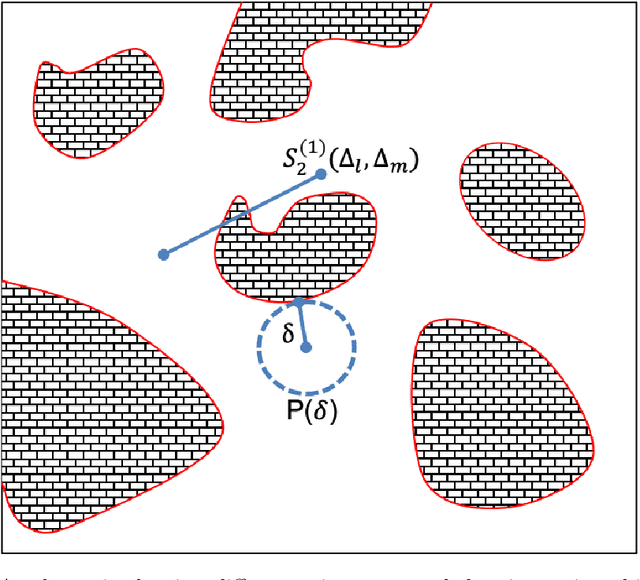
Stochastic microstructure reconstruction involves digital generation of microstructures that match key statistics and characteristics of a (set of) target microstructure(s). This process enables computational analyses on ensembles of microstructures without having to perform exhaustive and costly experimental characterizations. Statistical functions-based and deep learning-based methods are among the stochastic microstructure reconstruction approaches applicable to a wide range of material systems. In this paper, we integrate statistical descriptors as well as feature maps from a pre-trained deep neural network into an overall loss function for an optimization based reconstruction procedure. This helps us to achieve significant computational efficiency in reconstructing microstructures that retain the critically important physical properties of the target microstructure. A numerical example for the microstructure reconstruction of bi-phase random porous ceramic material demonstrates the efficiency of the proposed methodology. We further perform a detailed finite element analysis (FEA) of the reconstructed microstructures to calculate effective elastic modulus, effective thermal conductivity and effective hydraulic conductivity, in order to analyse the algorithm's capacity to capture the variability of these material properties with respect to those of the target microstructure. This method provides an economic, efficient and easy-to-use approach for reconstructing random multiphase materials in 2D which has the potential to be extended to 3D structures.

Probabilistic modeling of discrete structural response with application to composite plate penetration models

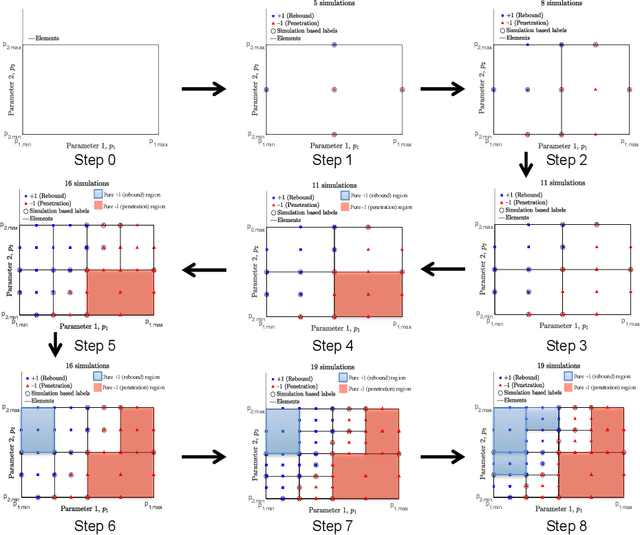
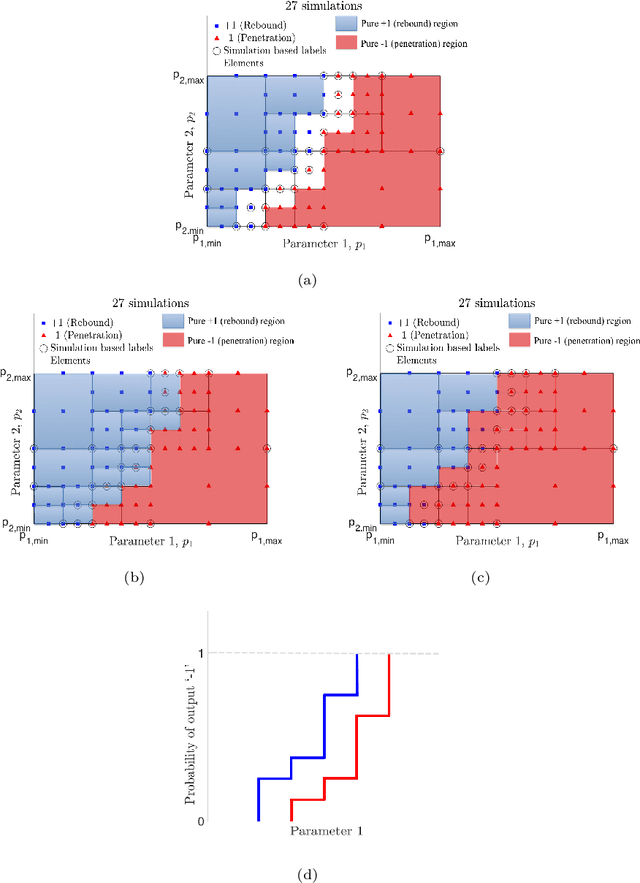
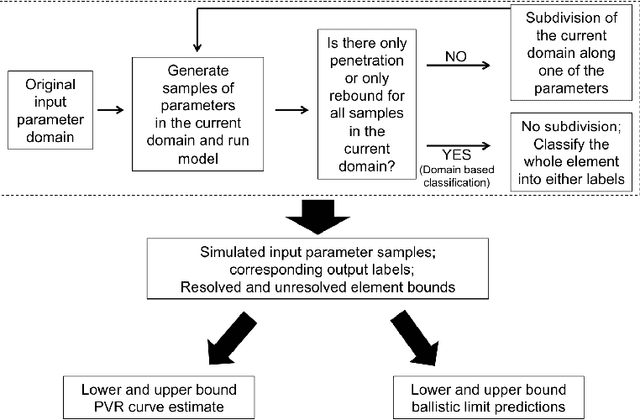
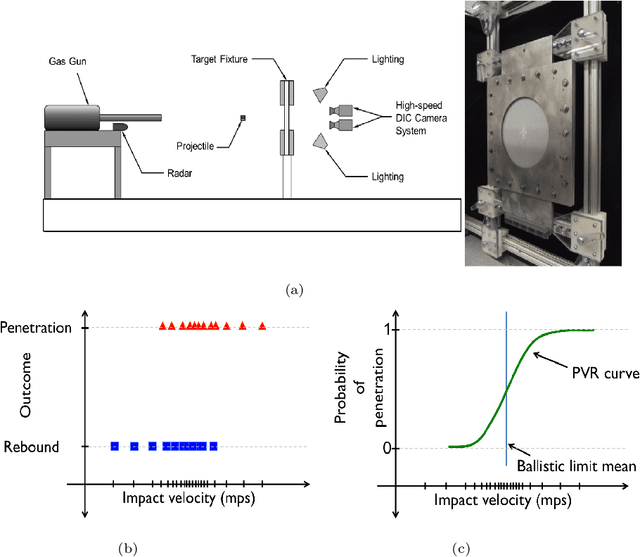
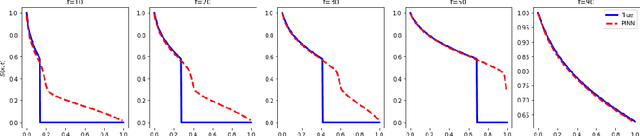
Discrete response of structures is often a key probabilistic quantity of interest. For example, one may need to identify the probability of a binary event, such as, whether a structure has buckled or not. In this study, an adaptive domain-based decomposition and classification method, combined with sparse grid sampling, is used to develop an efficient classification surrogate modeling algorithm for such discrete outputs. An assumption of monotonic behaviour of the output with respect to all model parameters, based on the physics of the problem, helps to reduce the number of model evaluations and makes the algorithm more efficient. As an application problem, this paper deals with the development of a computational framework for generation of probabilistic penetration response of S-2 glass/SC-15 epoxy composite plates under ballistic impact. This enables the computationally feasible generation of the probabilistic velocity response (PVR) curve or the $V_0-V_{100}$ curve as a function of the impact velocity, and the ballistic limit velocity prediction as a function of the model parameters. The PVR curve incorporates the variability of the model input parameters and describes the probability of penetration of the plate as a function of impact velocity.