Targeted Deep Architectures: A TMLE-Based Framework for Robust Causal Inference in Neural Networks

Modern deep neural networks are powerful predictive tools yet often lack valid inference for causal parameters, such as treatment effects or entire survival curves. While frameworks like Double Machine Learning (DML) and Targeted Maximum Likelihood Estimation (TMLE) can debias machine-learning fits, existing neural implementations either rely on "targeted losses" that do not guarantee solving the efficient influence function equation or computationally expensive post-hoc "fluctuations" for multi-parameter settings. We propose Targeted Deep Architectures (TDA), a new framework that embeds TMLE directly into the network's parameter space with no restrictions on the backbone architecture. Specifically, TDA partitions model parameters - freezing all but a small "targeting" subset - and iteratively updates them along a targeting gradient, derived from projecting the influence functions onto the span of the gradients of the loss with respect to weights. This procedure yields plug-in estimates that remove first-order bias and produce asymptotically valid confidence intervals. Crucially, TDA easily extends to multi-dimensional causal estimands (e.g., entire survival curves) by merging separate targeting gradients into a single universal targeting update. Theoretically, TDA inherits classical TMLE properties, including double robustness and semiparametric efficiency. Empirically, on the benchmark IHDP dataset (average treatment effects) and simulated survival data with informative censoring, TDA reduces bias and improves coverage relative to both standard neural-network estimators and prior post-hoc approaches. In doing so, TDA establishes a direct, scalable pathway toward rigorous causal inference within modern deep architectures for complex multi-parameter targets.

Highly Adaptive Ridge

In this paper we propose the Highly Adaptive Ridge (HAR): a regression method that achieves a $n^{-1/3}$ dimension-free L2 convergence rate in the class of right-continuous functions with square-integrable sectional derivatives. This is a large nonparametric function class that is particularly appropriate for tabular data. HAR is exactly kernel ridge regression with a specific data-adaptive kernel based on a saturated zero-order tensor-product spline basis expansion. We use simulation and real data to confirm our theory. We demonstrate empirical performance better than state-of-the-art algorithms for small datasets in particular.

Large Language Models as Co-Pilots for Causal Inference in Medical Studies

The validity of medical studies based on real-world clinical data, such as observational studies, depends on critical assumptions necessary for drawing causal conclusions about medical interventions. Many published studies are flawed because they violate these assumptions and entail biases such as residual confounding, selection bias, and misalignment between treatment and measurement times. Although researchers are aware of these pitfalls, they continue to occur because anticipating and addressing them in the context of a specific study can be challenging without a large, often unwieldy, interdisciplinary team with extensive expertise. To address this expertise gap, we explore the use of large language models (LLMs) as co-pilot tools to assist researchers in identifying study design flaws that undermine the validity of causal inferences. We propose a conceptual framework for LLMs as causal co-pilots that encode domain knowledge across various fields, engaging with researchers in natural language interactions to provide contextualized assistance in study design. We provide illustrative examples of how LLMs can function as causal co-pilots, propose a structured framework for their grounding in existing causal inference frameworks, and highlight the unique challenges and opportunities in adapting LLMs for reliable use in epidemiological research.

Adaptive-TMLE for the Average Treatment Effect based on Randomized Controlled Trial Augmented with Real-World Data

We consider the problem of estimating the average treatment effect (ATE) when both randomized control trial (RCT) data and real-world data (RWD) are available. We decompose the ATE estimand as the difference between a pooled-ATE estimand that integrates RCT and RWD and a bias estimand that captures the conditional effect of RCT enrollment on the outcome. We introduce an adaptive targeted minimum loss-based estimation (A-TMLE) framework to estimate them. We prove that the A-TMLE estimator is root-n-consistent and asymptotically normal. Moreover, in finite sample, it achieves the super-efficiency one would obtain had one known the oracle model for the conditional effect of the RCT enrollment on the outcome. Consequently, the smaller the working model of the bias induced by the RWD is, the greater our estimator's efficiency, while our estimator will always be at least as efficient as an efficient estimator that uses the RCT data only. A-TMLE outperforms existing methods in simulations by having smaller mean-squared-error and 95% confidence intervals. A-TMLE could help utilize RWD to improve the efficiency of randomized trial results without biasing the estimates of intervention effects. This approach could allow for smaller, faster trials, decreasing the time until patients can receive effective treatments.

Longitudinal Targeted Minimum Loss-based Estimation with Temporal-Difference Heterogeneous Transformer

We propose Deep Longitudinal Targeted Minimum Loss-based Estimation (Deep LTMLE), a novel approach to estimate the counterfactual mean of outcome under dynamic treatment policies in longitudinal problem settings. Our approach utilizes a transformer architecture with heterogeneous type embedding trained using temporal-difference learning. After obtaining an initial estimate using the transformer, following the targeted minimum loss-based likelihood estimation (TMLE) framework, we statistically corrected for the bias commonly associated with machine learning algorithms. Furthermore, our method also facilitates statistical inference by enabling the provision of 95% confidence intervals grounded in asymptotic statistical theory. Simulation results demonstrate our method's superior performance over existing approaches, particularly in complex, long time-horizon scenarios. It remains effective in small-sample, short-duration contexts, matching the performance of asymptotically efficient estimators. To demonstrate our method in practice, we applied our method to estimate counterfactual mean outcomes for standard versus intensive blood pressure management strategies in a real-world cardiovascular epidemiology cohort study.

Conformal Meta-learners for Predictive Inference of Individual Treatment Effects

We investigate the problem of machine learning-based (ML) predictive inference on individual treatment effects (ITEs). Previous work has focused primarily on developing ML-based meta-learners that can provide point estimates of the conditional average treatment effect (CATE); these are model-agnostic approaches for combining intermediate nuisance estimates to produce estimates of CATE. In this paper, we develop conformal meta-learners, a general framework for issuing predictive intervals for ITEs by applying the standard conformal prediction (CP) procedure on top of CATE meta-learners. We focus on a broad class of meta-learners based on two-stage pseudo-outcome regression and develop a stochastic ordering framework to study their validity. We show that inference with conformal meta-learners is marginally valid if their (pseudo outcome) conformity scores stochastically dominate oracle conformity scores evaluated on the unobserved ITEs. Additionally, we prove that commonly used CATE meta-learners, such as the doubly-robust learner, satisfy a model- and distribution-free stochastic (or convex) dominance condition, making their conformal inferences valid for practically-relevant levels of target coverage. Whereas existing procedures conduct inference on nuisance parameters (i.e., potential outcomes) via weighted CP, conformal meta-learners enable direct inference on the target parameter (ITE). Numerical experiments show that conformal meta-learners provide valid intervals with competitive efficiency while retaining the favorable point estimation properties of CATE meta-learners.

Adaptive debiased machine learning using data-driven model selection techniques

Debiased machine learning estimators for nonparametric inference of smooth functionals of the data-generating distribution can suffer from excessive variability and instability. For this reason, practitioners may resort to simpler models based on parametric or semiparametric assumptions. However, such simplifying assumptions may fail to hold, and estimates may then be biased due to model misspecification. To address this problem, we propose Adaptive Debiased Machine Learning (ADML), a nonparametric framework that combines data-driven model selection and debiased machine learning techniques to construct asymptotically linear, adaptive, and superefficient estimators for pathwise differentiable functionals. By learning model structure directly from data, ADML avoids the bias introduced by model misspecification and remains free from the restrictions of parametric and semiparametric models. While they may exhibit irregular behavior for the target parameter in a nonparametric statistical model, we demonstrate that ADML estimators provides regular and locally uniformly valid inference for a projection-based oracle parameter. Importantly, this oracle parameter agrees with the original target parameter for distributions within an unknown but correctly specified oracle statistical submodel that is learned from the data. This finding implies that there is no penalty, in a local asymptotic sense, for conducting data-driven model selection compared to having prior knowledge of the oracle submodel and oracle parameter. To demonstrate the practical applicability of our theory, we provide a broad class of ADML estimators for estimating the average treatment effect in adaptive partially linear regression models.

The Selectively Adaptive Lasso

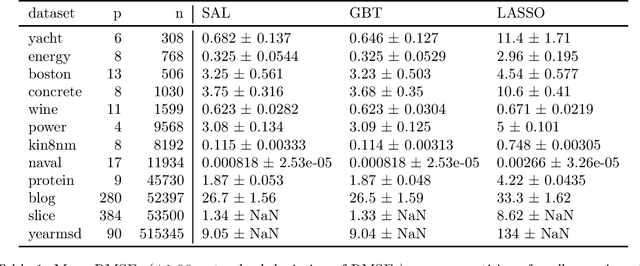
Machine learning regression methods allow estimation of functions without unrealistic parametric assumptions. Although they can perform exceptionally in prediction error, most lack theoretical convergence rates necessary for semi-parametric efficient estimation (e.g. TMLE, AIPW) of parameters like average treatment effects. The Highly Adaptive Lasso (HAL) is the only regression method proven to converge quickly enough for a meaningfully large class of functions, independent of the dimensionality of the predictors. Unfortunately, HAL is not computationally scalable. In this paper we build upon the theory of HAL to construct the Selectively Adaptive Lasso (SAL), a new algorithm which retains HAL's dimension-free, nonparametric convergence rate but which also scales computationally to massive datasets. To accomplish this, we prove some general theoretical results pertaining to empirical loss minimization in nested Donsker classes. Our resulting algorithm is a form of gradient tree boosting with an adaptive learning rate, which makes it fast and trivial to implement with off-the-shelf software. Finally, we show that our algorithm retains the performance of standard gradient boosting on a diverse group of real-world datasets. SAL makes semi-parametric efficient estimators practically possible and theoretically justifiable in many big data settings.

Two-Stage TMLE to Reduce Bias and Improve Efficiency in Cluster Randomized Trials

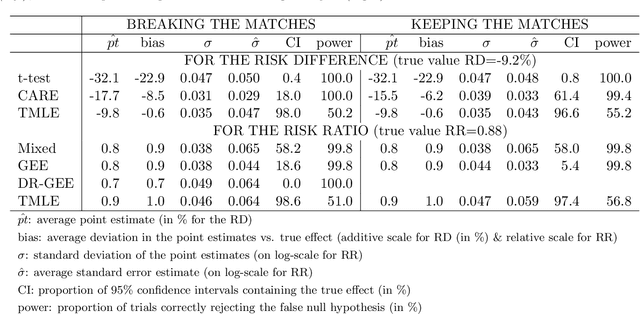
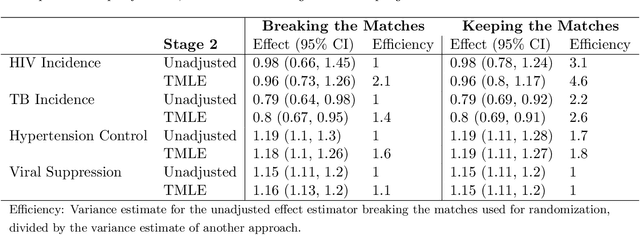
Cluster randomized trials (CRTs) randomly assign an intervention to groups of individuals (e.g., clinics or communities), and measure outcomes on individuals in those groups. While offering many advantages, this experimental design introduces challenges that are only partially addressed by existing analytic approaches. First, outcomes are often missing for some individuals within clusters. Failing to appropriately adjust for differential outcome measurement can result in biased estimates and inference. Second, CRTs often randomize limited numbers of clusters, resulting in chance imbalances on baseline outcome predictors between arms. Failing to adaptively adjust for these imbalances and other predictive covariates can result in efficiency losses. To address these methodological gaps, we propose and evaluate a novel two-stage targeted minimum loss-based estimator (TMLE) to adjust for baseline covariates in a manner that optimizes precision, after controlling for baseline and post-baseline causes of missing outcomes. Finite sample simulations illustrate that our approach can nearly eliminate bias due to differential outcome measurement, while other common CRT estimators yield misleading results and inferences. Application to real data from the SEARCH community randomized trial demonstrates the gains in efficiency afforded through adaptive adjustment for cluster-level covariates, after controlling for missingness on individual-level outcomes.

Risk Minimization from Adaptively Collected Data: Guarantees for Supervised and Policy Learning

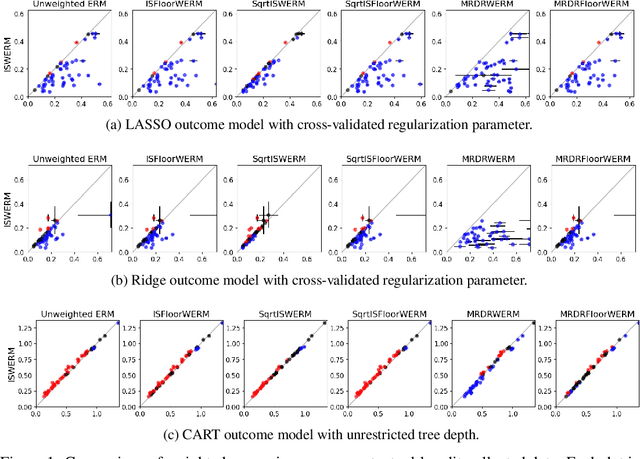
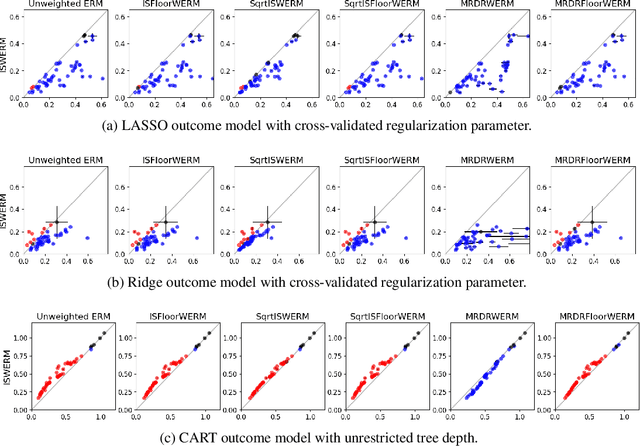
Empirical risk minimization (ERM) is the workhorse of machine learning, whether for classification and regression or for off-policy policy learning, but its model-agnostic guarantees can fail when we use adaptively collected data, such as the result of running a contextual bandit algorithm. We study a generic importance sampling weighted ERM algorithm for using adaptively collected data to minimize the average of a loss function over a hypothesis class and provide first-of-their-kind generalization guarantees and fast convergence rates. Our results are based on a new maximal inequality that carefully leverages the importance sampling structure to obtain rates with the right dependence on the exploration rate in the data. For regression, we provide fast rates that leverage the strong convexity of squared-error loss. For policy learning, we provide rate-optimal regret guarantees that close an open gap in the existing literature whenever exploration decays to zero, as is the case for bandit-collected data. An empirical investigation validates our theory.