BioNeMo Framework: a modular, high-performance library for AI model development in drug discovery

Artificial Intelligence models encoding biology and chemistry are opening new routes to high-throughput and high-quality in-silico drug development. However, their training increasingly relies on computational scale, with recent protein language models (pLM) training on hundreds of graphical processing units (GPUs). We introduce the BioNeMo Framework to facilitate the training of computational biology and chemistry AI models across hundreds of GPUs. Its modular design allows the integration of individual components, such as data loaders, into existing workflows and is open to community contributions. We detail technical features of the BioNeMo Framework through use cases such as pLM pre-training and fine-tuning. On 256 NVIDIA A100s, BioNeMo Framework trains a three billion parameter BERT-based pLM on over one trillion tokens in 4.2 days. The BioNeMo Framework is open-source and free for everyone to use.

EquiJump: Protein Dynamics Simulation via SO(3)-Equivariant Stochastic Interpolants

Mapping the conformational dynamics of proteins is crucial for elucidating their functional mechanisms. While Molecular Dynamics (MD) simulation enables detailed time evolution of protein motion, its computational toll hinders its use in practice. To address this challenge, multiple deep learning models for reproducing and accelerating MD have been proposed drawing on transport-based generative methods. However, existing work focuses on generation through transport of samples from prior distributions, that can often be distant from the data manifold. The recently proposed framework of stochastic interpolants, instead, enables transport between arbitrary distribution endpoints. Building upon this work, we introduce EquiJump, a transferable SO(3)-equivariant model that bridges all-atom protein dynamics simulation time steps directly. Our approach unifies diverse sampling methods and is benchmarked against existing models on trajectory data of fast folding proteins. EquiJump achieves state-of-the-art results on dynamics simulation with a transferable model on all of the fast folding proteins.

Symphony: Symmetry-Equivariant Point-Centered Spherical Harmonics for Molecule Generation

We present Symphony, an $E(3)$-equivariant autoregressive generative model for 3D molecular geometries that iteratively builds a molecule from molecular fragments. Existing autoregressive models such as G-SchNet and G-SphereNet for molecules utilize rotationally invariant features to respect the 3D symmetries of molecules. In contrast, Symphony uses message-passing with higher-degree $E(3)$-equivariant features. This allows a novel representation of probability distributions via spherical harmonic signals to efficiently model the 3D geometry of molecules. We show that Symphony is able to accurately generate small molecules from the QM9 dataset, outperforming existing autoregressive models and approaching the performance of diffusion models.

Ophiuchus: Scalable Modeling of Protein Structures through Hierarchical Coarse-graining SO(3)-Equivariant Autoencoders

Three-dimensional native states of natural proteins display recurring and hierarchical patterns. Yet, traditional graph-based modeling of protein structures is often limited to operate within a single fine-grained resolution, and lacks hourglass neural architectures to learn those high-level building blocks. We narrow this gap by introducing Ophiuchus, an SO(3)-equivariant coarse-graining model that efficiently operates on all heavy atoms of standard protein residues, while respecting their relevant symmetries. Our model departs from current approaches that employ graph modeling, instead focusing on local convolutional coarsening to model sequence-motif interactions in log-linear length complexity. We train Ophiuchus on contiguous fragments of PDB monomers, investigating its reconstruction capabilities across different compression rates. We examine the learned latent space and demonstrate its prompt usage in conformational interpolation, comparing interpolated trajectories to structure snapshots from the PDBFlex dataset. Finally, we leverage denoising diffusion probabilistic models (DDPM) to efficiently sample readily-decodable latent embeddings of diverse miniproteins. Our experiments demonstrate Ophiuchus to be a scalable basis for efficient protein modeling and generation.

A General Framework for Equivariant Neural Networks on Reductive Lie Groups

Reductive Lie Groups, such as the orthogonal groups, the Lorentz group, or the unitary groups, play essential roles across scientific fields as diverse as high energy physics, quantum mechanics, quantum chromodynamics, molecular dynamics, computer vision, and imaging. In this paper, we present a general Equivariant Neural Network architecture capable of respecting the symmetries of the finite-dimensional representations of any reductive Lie Group G. Our approach generalizes the successful ACE and MACE architectures for atomistic point clouds to any data equivariant to a reductive Lie group action. We also introduce the lie-nn software library, which provides all the necessary tools to develop and implement such general G-equivariant neural networks. It implements routines for the reduction of generic tensor products of representations into irreducible representations, making it easy to apply our architecture to a wide range of problems and groups. The generality and performance of our approach are demonstrated by applying it to the tasks of top quark decay tagging (Lorentz group) and shape recognition (orthogonal group).

An end-to-end SE-equivariant segmentation network

Convolutional neural networks (CNNs) allow for parameter sharing and translational equivariance by using convolutional kernels in their linear layers. By restricting these kernels to be SO(3)-steerable, CNNs can further improve parameter sharing and equivariance. These equivariant convolutional layers have several advantages over standard convolutional layers, including increased robustness to unseen poses, smaller network size, and improved sample efficiency. Despite this, most segmentation networks used in medical image analysis continue to rely on standard convolutional kernels. In this paper, we present a new family of segmentation networks that use equivariant voxel convolutions based on spherical harmonics, as well as equivariant pooling and normalization operations. These SE(3)-equivariant volumetric segmentation networks, which are robust to data poses not seen during training, do not require rotation-based data augmentation during training. In addition, we demonstrate improved segmentation performance in MRI brain tumor and healthy brain structure segmentation tasks, with enhanced robustness to reduced amounts of training data and improved parameter efficiency. Code to reproduce our results, and to implement the equivariant segmentation networks for other tasks is available at http://github.com/SCAN-NRAD/e3nn_Unet

Dissecting the Effects of SGD Noise in Distinct Regimes of Deep Learning

Understanding when the noise in stochastic gradient descent (SGD) affects generalization of deep neural networks remains a challenge, complicated by the fact that networks can operate in distinct training regimes. Here we study how the magnitude of this noise $T$ affects performance as the size of the training set $P$ and the scale of initialization $\alpha$ are varied. For gradient descent, $\alpha$ is a key parameter that controls if the network is `lazy' ($\alpha\gg 1$) or instead learns features ($\alpha\ll 1$). For classification of MNIST and CIFAR10 images, our central results are: (i) obtaining phase diagrams for performance in the $(\alpha,T)$ plane. They show that SGD noise can be detrimental or instead useful depending on the training regime. Moreover, although increasing $T$ or decreasing $\alpha$ both allow the net to escape the lazy regime, these changes can have opposite effects on performance. (ii) Most importantly, we find that key dynamical quantities (including the total variations of weights during training) depend on both $T$ and $P$ as power laws, and the characteristic temperature $T_c$, where the noise of SGD starts affecting performance, is a power law of $P$. These observations indicate that a key effect of SGD noise occurs late in training, by affecting the stopping process whereby all data are fitted. We argue that due to SGD noise, nets must develop a stronger `signal', i.e. larger informative weights, to fit the data, leading to a longer training time. The same effect occurs at larger training set $P$. We confirm this view in the perceptron model, where signal and noise can be precisely measured. Interestingly, exponents characterizing the effect of SGD depend on the density of data near the decision boundary, as we explain.

e3nn: Euclidean Neural Networks

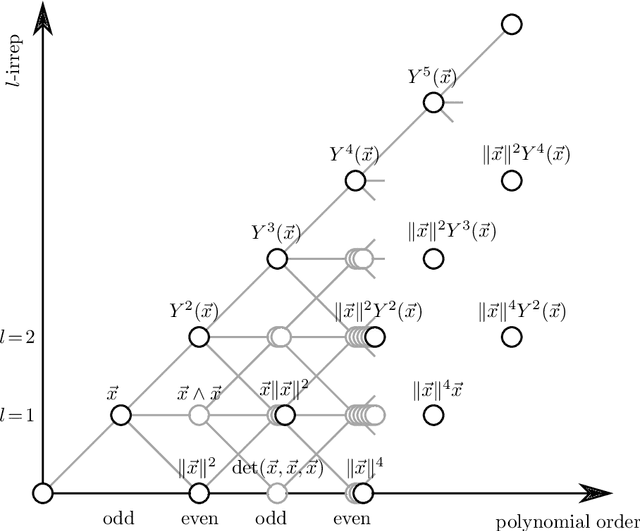
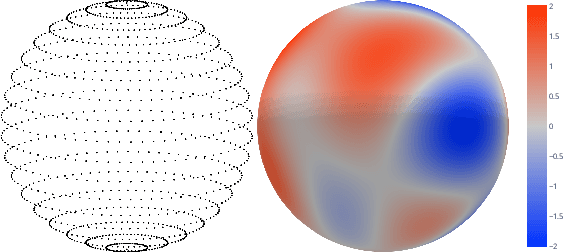
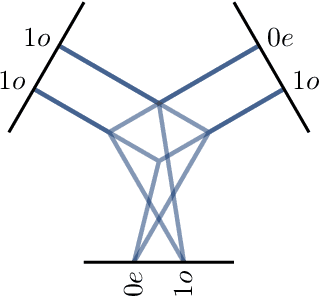
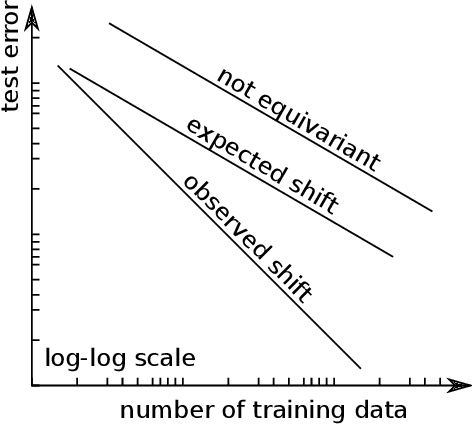
We present e3nn, a generalized framework for creating E(3) equivariant trainable functions, also known as Euclidean neural networks. e3nn naturally operates on geometry and geometric tensors that describe systems in 3D and transform predictably under a change of coordinate system. The core of e3nn are equivariant operations such as the TensorProduct class or the spherical harmonics functions that can be composed to create more complex modules such as convolutions and attention mechanisms. These core operations of e3nn can be used to efficiently articulate Tensor Field Networks, 3D Steerable CNNs, Clebsch-Gordan Networks, SE(3) Transformers and other E(3) equivariant networks.

How memory architecture affects performance and learning in simple POMDPs

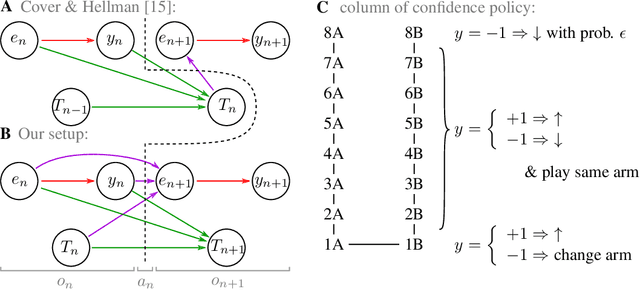
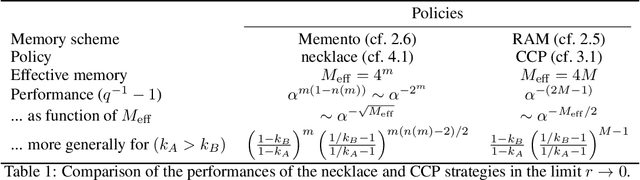
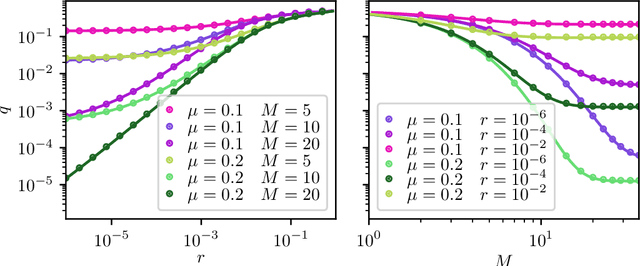
Reinforcement learning is made much more complex when the agent's observation is partial or noisy. This case corresponds to a partially observable Markov decision process (POMDP). One strategy to seek good performance in POMDPs is to endow the agent with a finite memory, whose update is governed by the policy. However, policy optimization is non-convex in that case and can lead to poor training performance for random initialization. The performance can be empirically improved by constraining the memory architecture, then sacrificing optimality to facilitate training. Here we study this trade-off in the two-arm bandit problem, and compare two extreme cases: (i) the random access memory where any transitions between $M$ memory states are allowed and (ii) a fixed memory where the agent can access its last $m$ actions and rewards. For (i), the probability $q$ to play the worst arm is known to be exponentially small in $M$ for the optimal policy. Our main result is to show that similar performance can be reached for (ii) as well, despite the simplicity of the memory architecture: using a conjecture on Gray-ordered binary necklaces, we find policies for which $q$ is exponentially small in $2^m$ i.e. $q\sim\alpha^{2^m}$ for some $\alpha < 1$. Interestingly, we observe empirically that training from random initialization leads to very poor results for (i), and significantly better results for (ii).

SE(3)-equivariant prediction of molecular wavefunctions and electronic densities

Machine learning has enabled the prediction of quantum chemical properties with high accuracy and efficiency, allowing to bypass computationally costly ab initio calculations. Instead of training on a fixed set of properties, more recent approaches attempt to learn the electronic wavefunction (or density) as a central quantity of atomistic systems, from which all other observables can be derived. This is complicated by the fact that wavefunctions transform non-trivially under molecular rotations, which makes them a challenging prediction target. To solve this issue, we introduce general SE(3)-equivariant operations and building blocks for constructing deep learning architectures for geometric point cloud data and apply them to reconstruct wavefunctions of atomistic systems with unprecedented accuracy. Our model reduces prediction errors by up to two orders of magnitude compared to the previous state-of-the-art and makes it possible to derive properties such as energies and forces directly from the wavefunction in an end-to-end manner. We demonstrate the potential of our approach in a transfer learning application, where a model trained on low accuracy reference wavefunctions implicitly learns to correct for electronic many-body interactions from observables computed at a higher level of theory. Such machine-learned wavefunction surrogates pave the way towards novel semi-empirical methods, offering resolution at an electronic level while drastically decreasing computational cost. While we focus on physics applications in this contribution, the proposed equivariant framework for deep learning on point clouds is promising also beyond, say, in computer vision or graphics.