How memory architecture affects performance and learning in simple POMDPs
Paper and Code
Jun 16, 2021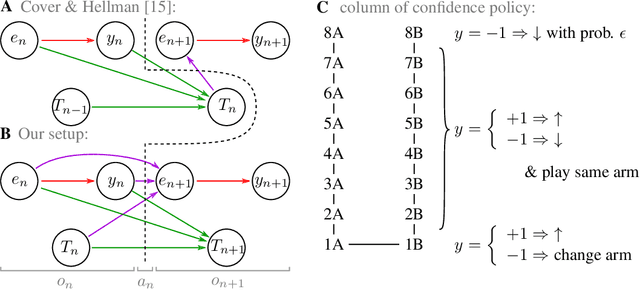
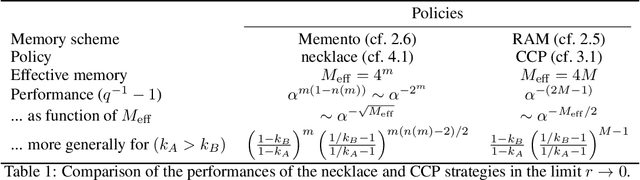
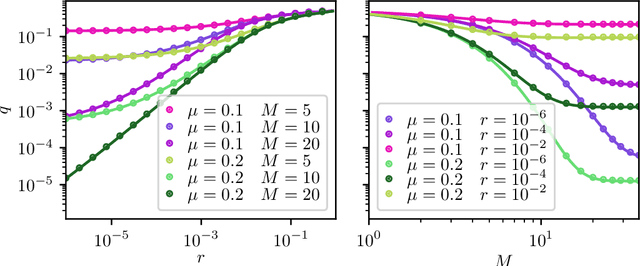

Reinforcement learning is made much more complex when the agent's observation is partial or noisy. This case corresponds to a partially observable Markov decision process (POMDP). One strategy to seek good performance in POMDPs is to endow the agent with a finite memory, whose update is governed by the policy. However, policy optimization is non-convex in that case and can lead to poor training performance for random initialization. The performance can be empirically improved by constraining the memory architecture, then sacrificing optimality to facilitate training. Here we study this trade-off in the two-arm bandit problem, and compare two extreme cases: (i) the random access memory where any transitions between $M$ memory states are allowed and (ii) a fixed memory where the agent can access its last $m$ actions and rewards. For (i), the probability $q$ to play the worst arm is known to be exponentially small in $M$ for the optimal policy. Our main result is to show that similar performance can be reached for (ii) as well, despite the simplicity of the memory architecture: using a conjecture on Gray-ordered binary necklaces, we find policies for which $q$ is exponentially small in $2^m$ i.e. $q\sim\alpha^{2^m}$ for some $\alpha < 1$. Interestingly, we observe empirically that training from random initialization leads to very poor results for (i), and significantly better results for (ii).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge