Robust Feature Selection by Mutual Information Distributions

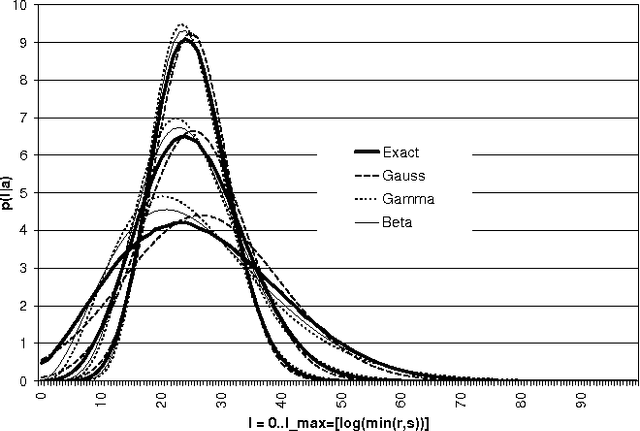
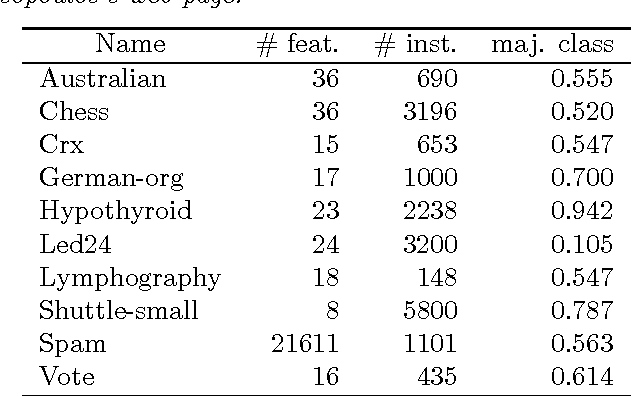
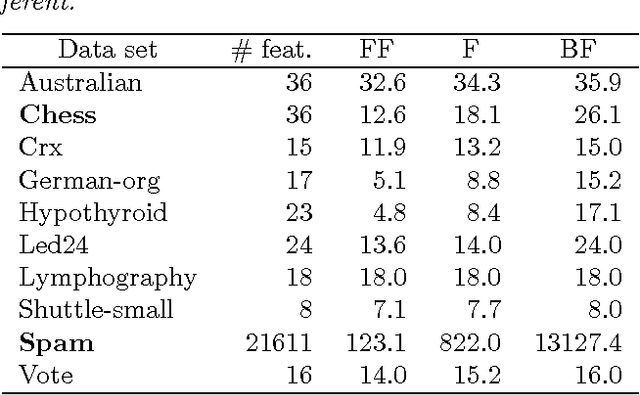
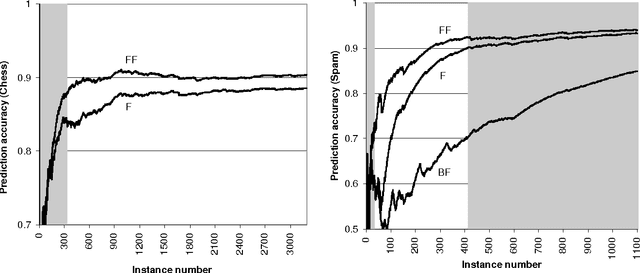
Mutual information is widely used in artificial intelligence, in a descriptive way, to measure the stochastic dependence of discrete random variables. In order to address questions such as the reliability of the empirical value, one must consider sample-to-population inferential approaches. This paper deals with the distribution of mutual information, as obtained in a Bayesian framework by a second-order Dirichlet prior distribution. The exact analytical expression for the mean and an analytical approximation of the variance are reported. Asymptotic approximations of the distribution are proposed. The results are applied to the problem of selecting features for incremental learning and classification of the naive Bayes classifier. A fast, newly defined method is shown to outperform the traditional approach based on empirical mutual information on a number of real data sets. Finally, a theoretical development is reported that allows one to efficiently extend the above methods to incomplete samples in an easy and effective way.

Extreme State Aggregation Beyond MDPs

We consider a Reinforcement Learning setup where an agent interacts with an environment in observation-reward-action cycles without any (esp.\ MDP) assumptions on the environment. State aggregation and more generally feature reinforcement learning is concerned with mapping histories/raw-states to reduced/aggregated states. The idea behind both is that the resulting reduced process (approximately) forms a small stationary finite-state MDP, which can then be efficiently solved or learnt. We considerably generalize existing aggregation results by showing that even if the reduced process is not an MDP, the (q-)value functions and (optimal) policies of an associated MDP with same state-space size solve the original problem, as long as the solution can approximately be represented as a function of the reduced states. This implies an upper bound on the required state space size that holds uniformly for all RL problems. It may also explain why RL algorithms designed for MDPs sometimes perform well beyond MDPs.

Offline to Online Conversion

We consider the problem of converting offline estimators into an online predictor or estimator with small extra regret. Formally this is the problem of merging a collection of probability measures over strings of length 1,2,3,... into a single probability measure over infinite sequences. We describe various approaches and their pros and cons on various examples. As a side-result we give an elementary non-heuristic purely combinatoric derivation of Turing's famous estimator. Our main technical contribution is to determine the computational complexity of online estimators with good guarantees in general.

Online Learning of k-CNF Boolean Functions

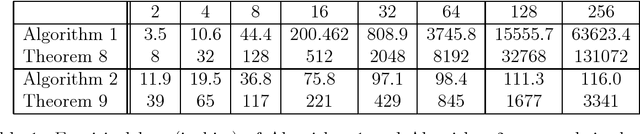
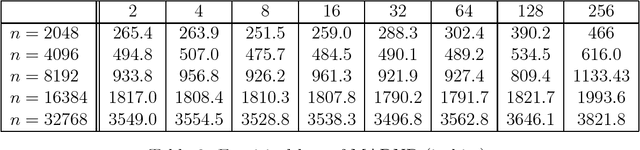
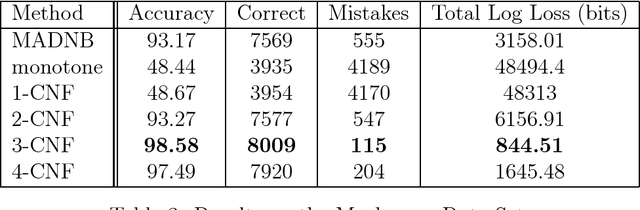
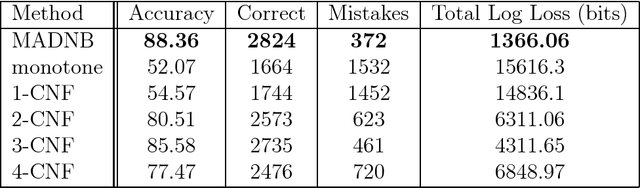
This paper revisits the problem of learning a k-CNF Boolean function from examples in the context of online learning under the logarithmic loss. In doing so, we give a Bayesian interpretation to one of Valiant's celebrated PAC learning algorithms, which we then build upon to derive two efficient, online, probabilistic, supervised learning algorithms for predicting the output of an unknown k-CNF Boolean function. We analyze the loss of our methods, and show that the cumulative log-loss can be upper bounded, ignoring logarithmic factors, by a polynomial function of the size of each example.

A Novel Illumination-Invariant Loss for Monocular 3D Pose Estimation

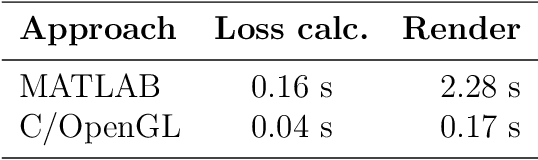
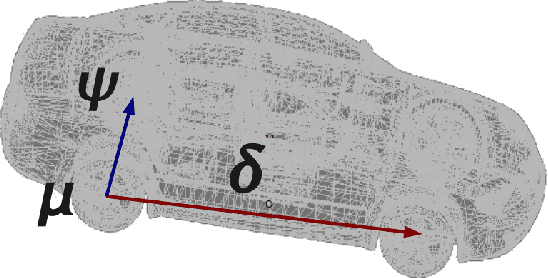
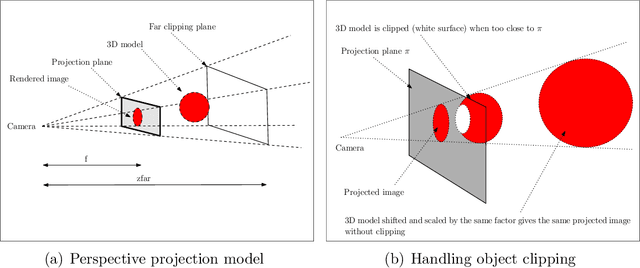
The problem of identifying the 3D pose of a known object from a given 2D image has important applications in Computer Vision. Our proposed method of registering a 3D model of a known object on a given 2D photo of the object has numerous advantages over existing methods. It does not require prior training, knowledge of the camera parameters, explicit point correspondences or matching features between the image and model. Unlike techniques that estimate a partial 3D pose (as in an overhead view of traffic or machine parts on a conveyor belt), our method estimates the complete 3D pose of the object. It works on a single static image from a given view under varying and unknown lighting conditions. For this purpose we derive a novel illumination-invariant distance measure between the 2D photo and projected 3D model, which is then minimised to find the best pose parameters. Results for vehicle pose detection in real photographs are presented.

The Sample-Complexity of General Reinforcement Learning

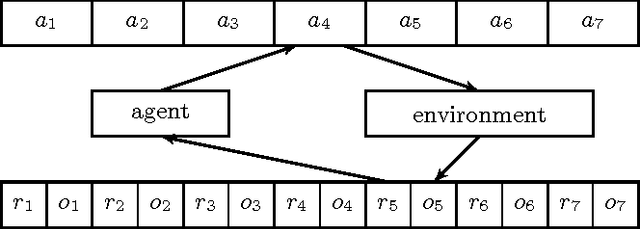
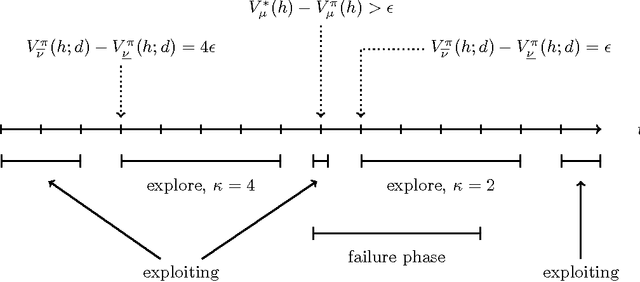
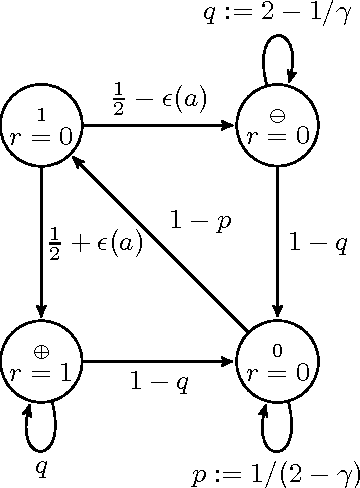
We present a new algorithm for general reinforcement learning where the true environment is known to belong to a finite class of N arbitrary models. The algorithm is shown to be near-optimal for all but O(N log^2 N) time-steps with high probability. Infinite classes are also considered where we show that compactness is a key criterion for determining the existence of uniform sample-complexity bounds. A matching lower bound is given for the finite case.

Concentration and Confidence for Discrete Bayesian Sequence Predictors

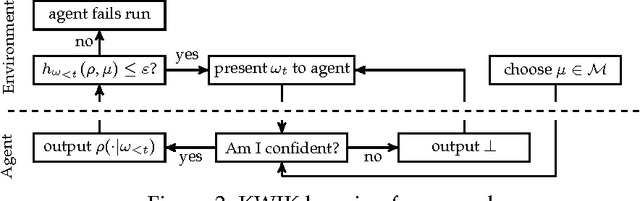
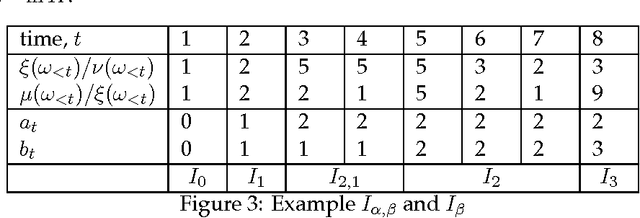
Bayesian sequence prediction is a simple technique for predicting future symbols sampled from an unknown measure on infinite sequences over a countable alphabet. While strong bounds on the expected cumulative error are known, there are only limited results on the distribution of this error. We prove tight high-probability bounds on the cumulative error, which is measured in terms of the Kullback-Leibler (KL) divergence. We also consider the problem of constructing upper confidence bounds on the KL and Hellinger errors similar to those constructed from Hoeffding-like bounds in the i.i.d. case. The new results are applied to show that Bayesian sequence prediction can be used in the Knows What It Knows (KWIK) framework with bounds that match the state-of-the-art.

Optimistic Agents are Asymptotically Optimal

We use optimism to introduce generic asymptotically optimal reinforcement learning agents. They achieve, with an arbitrary finite or compact class of environments, asymptotically optimal behavior. Furthermore, in the finite deterministic case we provide finite error bounds.

Probabilities on Sentences in an Expressive Logic

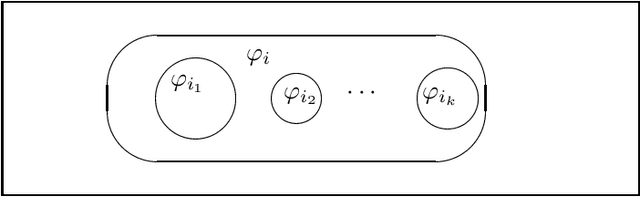
Automated reasoning about uncertain knowledge has many applications. One difficulty when developing such systems is the lack of a completely satisfactory integration of logic and probability. We address this problem directly. Expressive languages like higher-order logic are ideally suited for representing and reasoning about structured knowledge. Uncertain knowledge can be modeled by using graded probabilities rather than binary truth-values. The main technical problem studied in this paper is the following: Given a set of sentences, each having some probability of being true, what probability should be ascribed to other (query) sentences? A natural wish-list, among others, is that the probability distribution (i) is consistent with the knowledge base, (ii) allows for a consistent inference procedure and in particular (iii) reduces to deductive logic in the limit of probabilities being 0 and 1, (iv) allows (Bayesian) inductive reasoning and (v) learning in the limit and in particular (vi) allows confirmation of universally quantified hypotheses/sentences. We translate this wish-list into technical requirements for a prior probability and show that probabilities satisfying all our criteria exist. We also give explicit constructions and several general characterizations of probabilities that satisfy some or all of the criteria and various (counter) examples. We also derive necessary and sufficient conditions for extending beliefs about finitely many sentences to suitable probabilities over all sentences, and in particular least dogmatic or least biased ones. We conclude with a brief outlook on how the developed theory might be used and approximated in autonomous reasoning agents. Our theory is a step towards a globally consistent and empirically satisfactory unification of probability and logic.

Can Intelligence Explode?

The technological singularity refers to a hypothetical scenario in which technological advances virtually explode. The most popular scenario is the creation of super-intelligent algorithms that recursively create ever higher intelligences. It took many decades for these ideas to spread from science fiction to popular science magazines and finally to attract the attention of serious philosophers. David Chalmers' (JCS 2010) article is the first comprehensive philosophical analysis of the singularity in a respected philosophy journal. The motivation of my article is to augment Chalmers' and to discuss some issues not addressed by him, in particular what it could mean for intelligence to explode. In this course, I will (have to) provide a more careful treatment of what intelligence actually is, separate speed from intelligence explosion, compare what super-intelligent participants and classical human observers might experience and do, discuss immediate implications for the diversity and value of life, consider possible bounds on intelligence, and contemplate intelligences right at the singularity.