Avoiding Wireheading with Value Reinforcement Learning

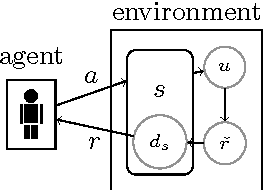
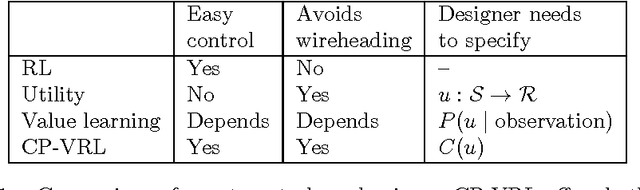
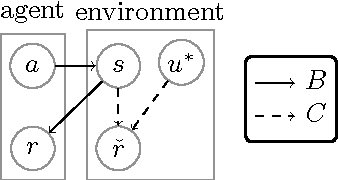
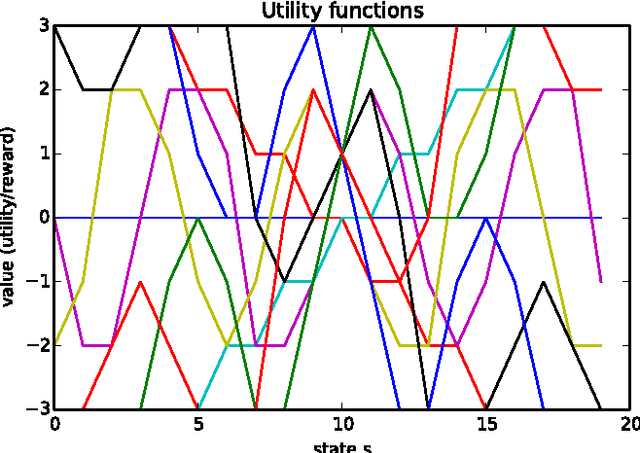
How can we design good goals for arbitrarily intelligent agents? Reinforcement learning (RL) is a natural approach. Unfortunately, RL does not work well for generally intelligent agents, as RL agents are incentivised to shortcut the reward sensor for maximum reward -- the so-called wireheading problem. In this paper we suggest an alternative to RL called value reinforcement learning (VRL). In VRL, agents use the reward signal to learn a utility function. The VRL setup allows us to remove the incentive to wirehead by placing a constraint on the agent's actions. The constraint is defined in terms of the agent's belief distributions, and does not require an explicit specification of which actions constitute wireheading.

Self-Modification of Policy and Utility Function in Rational Agents

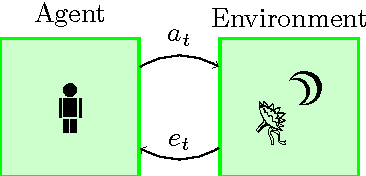
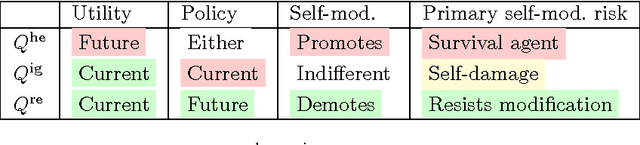
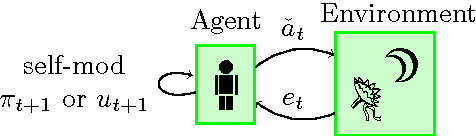
Any agent that is part of the environment it interacts with and has versatile actuators (such as arms and fingers), will in principle have the ability to self-modify -- for example by changing its own source code. As we continue to create more and more intelligent agents, chances increase that they will learn about this ability. The question is: will they want to use it? For example, highly intelligent systems may find ways to change their goals to something more easily achievable, thereby `escaping' the control of their designers. In an important paper, Omohundro (2008) argued that goal preservation is a fundamental drive of any intelligent system, since a goal is more likely to be achieved if future versions of the agent strive towards the same goal. In this paper, we formalise this argument in general reinforcement learning, and explore situations where it fails. Our conclusion is that the self-modification possibility is harmless if and only if the value function of the agent anticipates the consequences of self-modifications and use the current utility function when evaluating the future.

Loss Bounds and Time Complexity for Speed Priors

This paper establishes for the first time the predictive performance of speed priors and their computational complexity. A speed prior is essentially a probability distribution that puts low probability on strings that are not efficiently computable. We propose a variant to the original speed prior (Schmidhuber, 2002), and show that our prior can predict sequences drawn from probability measures that are estimable in polynomial time. Our speed prior is computable in doubly-exponential time, but not in polynomial time. On a polynomial time computable sequence our speed prior is computable in exponential time. We show better upper complexity bounds for Schmidhuber's speed prior under the same conditions, and that it predicts deterministic sequences that are computable in polynomial time; however, we also show that it is not computable in polynomial time, and the question of its predictive properties for stochastic sequences remains open.

On the Computability of AIXI

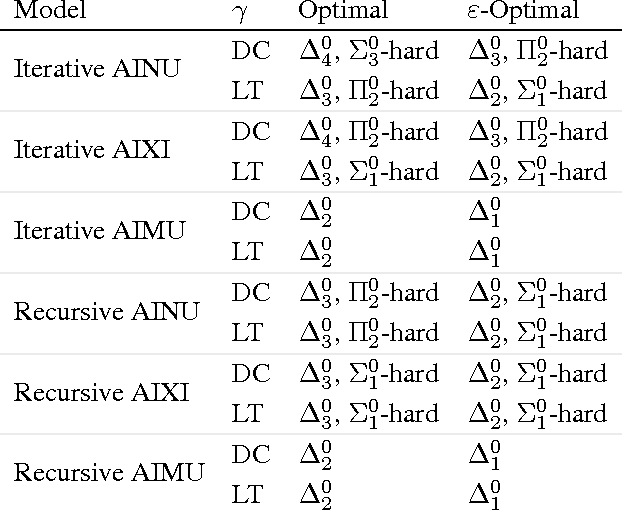
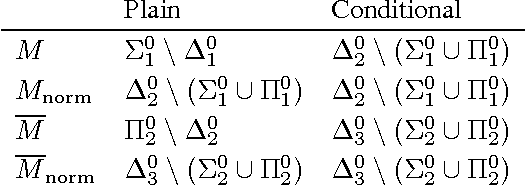
How could we solve the machine learning and the artificial intelligence problem if we had infinite computation? Solomonoff induction and the reinforcement learning agent AIXI are proposed answers to this question. Both are known to be incomputable. In this paper, we quantify this using the arithmetical hierarchy, and prove upper and corresponding lower bounds for incomputability. We show that AIXI is not limit computable, thus it cannot be approximated using finite computation. Our main result is a limit-computable {\epsilon}-optimal version of AIXI with infinite horizon that maximizes expected rewards.

Bad Universal Priors and Notions of Optimality

A big open question of algorithmic information theory is the choice of the universal Turing machine (UTM). For Kolmogorov complexity and Solomonoff induction we have invariance theorems: the choice of the UTM changes bounds only by a constant. For the universally intelligent agent AIXI (Hutter, 2005) no invariance theorem is known. Our results are entirely negative: we discuss cases in which unlucky or adversarial choices of the UTM cause AIXI to misbehave drastically. We show that Legg-Hutter intelligence and thus balanced Pareto optimality is entirely subjective, and that every policy is Pareto optimal in the class of all computable environments. This undermines all existing optimality properties for AIXI. While it may still serve as a gold standard for AI, our results imply that AIXI is a relative theory, dependent on the choice of the UTM.

On the Computability of Solomonoff Induction and Knowledge-Seeking

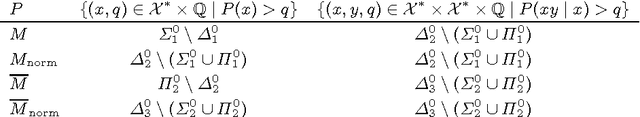
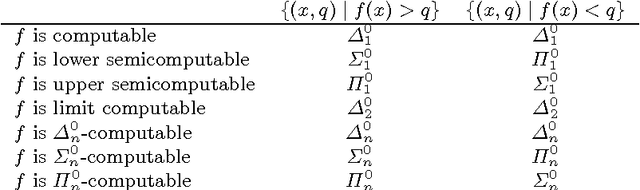
Solomonoff induction is held as a gold standard for learning, but it is known to be incomputable. We quantify its incomputability by placing various flavors of Solomonoff's prior M in the arithmetical hierarchy. We also derive computability bounds for knowledge-seeking agents, and give a limit-computable weakly asymptotically optimal reinforcement learning agent.

Solomonoff Induction Violates Nicod's Criterion

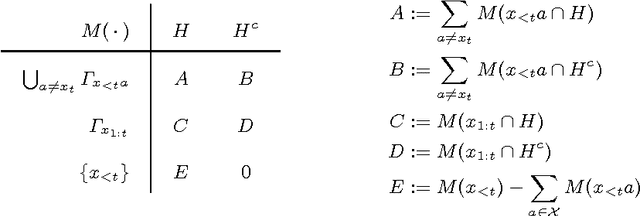
Nicod's criterion states that observing a black raven is evidence for the hypothesis H that all ravens are black. We show that Solomonoff induction does not satisfy Nicod's criterion: there are time steps in which observing black ravens decreases the belief in H. Moreover, while observing any computable infinite string compatible with H, the belief in H decreases infinitely often when using the unnormalized Solomonoff prior, but only finitely often when using the normalized Solomonoff prior. We argue that the fault is not with Solomonoff induction; instead we should reject Nicod's criterion.

Sequential Extensions of Causal and Evidential Decision Theory

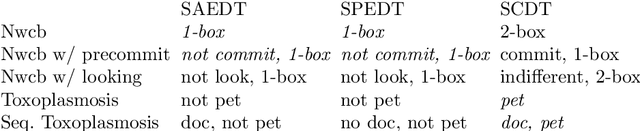
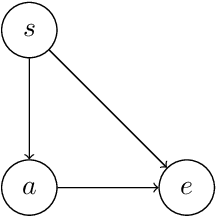
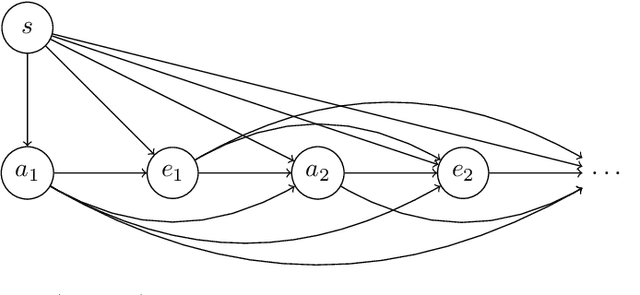
Moving beyond the dualistic view in AI where agent and environment are separated incurs new challenges for decision making, as calculation of expected utility is no longer straightforward. The non-dualistic decision theory literature is split between causal decision theory and evidential decision theory. We extend these decision algorithms to the sequential setting where the agent alternates between taking actions and observing their consequences. We find that evidential decision theory has two natural extensions while causal decision theory only has one.

Compress and Control

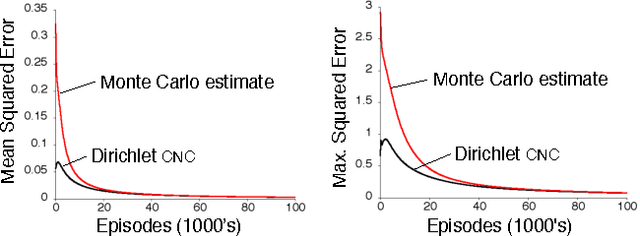
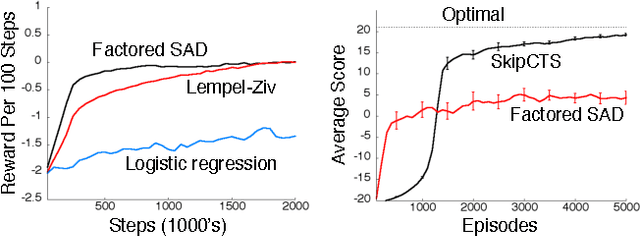
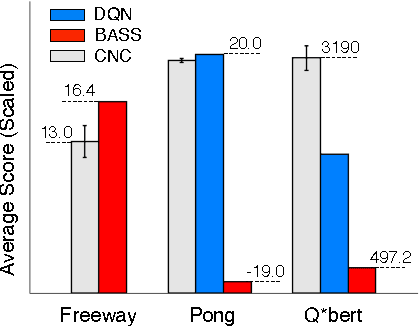
This paper describes a new information-theoretic policy evaluation technique for reinforcement learning. This technique converts any compression or density model into a corresponding estimate of value. Under appropriate stationarity and ergodicity conditions, we show that the use of a sufficiently powerful model gives rise to a consistent value function estimator. We also study the behavior of this technique when applied to various Atari 2600 video games, where the use of suboptimal modeling techniques is unavoidable. We consider three fundamentally different models, all too limited to perfectly model the dynamics of the system. Remarkably, we find that our technique provides sufficiently accurate value estimates for effective on-policy control. We conclude with a suggestive study highlighting the potential of our technique to scale to large problems.

Indefinitely Oscillating Martingales

We construct a class of nonnegative martingale processes that oscillate indefinitely with high probability. For these processes, we state a uniform rate of the number of oscillations and show that this rate is asymptotically close to the theoretical upper bound. These bounds on probability and expectation of the number of upcrossings are compared to classical bounds from the martingale literature. We discuss two applications. First, our results imply that the limit of the minimum description length operator may not exist. Second, we give bounds on how often one can change one's belief in a given hypothesis when observing a stream of data.