Graph Alignment for Benchmarking Graph Neural Networks and Learning Positional Encodings

We propose a novel benchmarking methodology for graph neural networks (GNNs) based on the graph alignment problem, a combinatorial optimization task that generalizes graph isomorphism by aligning two unlabeled graphs to maximize overlapping edges. We frame this problem as a self-supervised learning task and present several methods to generate graph alignment datasets using synthetic random graphs and real-world graph datasets from multiple domains. For a given graph dataset, we generate a family of graph alignment datasets with increasing difficulty, allowing us to rank the performance of various architectures. Our experiments indicate that anisotropic graph neural networks outperform standard convolutional architectures. To further demonstrate the utility of the graph alignment task, we show its effectiveness for unsupervised GNN pre-training, where the learned node embeddings outperform other positional encodings on three molecular regression tasks and achieve state-of-the-art results on the PCQM4Mv2 dataset with significantly fewer parameters. To support reproducibility and further research, we provide an open-source Python package to generate graph alignment datasets and benchmark new GNN architectures.

Random Sparse Lifts: Construction, Analysis and Convergence of finite sparse networks

We present a framework to define a large class of neural networks for which, by construction, training by gradient flow provably reaches arbitrarily low loss when the number of parameters grows. Distinct from the fixed-space global optimality of non-convex optimization, this new form of convergence, and the techniques introduced to prove such convergence, pave the way for a usable deep learning convergence theory in the near future, without overparameterization assumptions relating the number of parameters and training samples. We define these architectures from a simple computation graph and a mechanism to lift it, thus increasing the number of parameters, generalizing the idea of increasing the widths of multi-layer perceptrons. We show that architectures similar to most common deep learning models are present in this class, obtained by sparsifying the weight tensors of usual architectures at initialization. Leveraging tools of algebraic topology and random graph theory, we use the computation graph's geometry to propagate properties guaranteeing convergence to any precision for these large sparse models.

Neural Incremental Data Assimilation

Data assimilation is a central problem in many geophysical applications, such as weather forecasting. It aims to estimate the state of a potentially large system, such as the atmosphere, from sparse observations, supplemented by prior physical knowledge. The size of the systems involved and the complexity of the underlying physical equations make it a challenging task from a computational point of view. Neural networks represent a promising method of emulating the physics at low cost, and therefore have the potential to considerably improve and accelerate data assimilation. In this work, we introduce a deep learning approach where the physical system is modeled as a sequence of coarse-to-fine Gaussian prior distributions parametrized by a neural network. This allows us to define an assimilation operator, which is trained in an end-to-end fashion to minimize the reconstruction error on a dataset with different observation processes. We illustrate our approach on chaotic dynamical physical systems with sparse observations, and compare it to traditional variational data assimilation methods.

Automatic Rao-Blackwellization for Sequential Monte Carlo with Belief Propagation

Exact Bayesian inference on state-space models~(SSM) is in general untractable, and unfortunately, basic Sequential Monte Carlo~(SMC) methods do not yield correct approximations for complex models. In this paper, we propose a mixed inference algorithm that computes closed-form solutions using belief propagation as much as possible, and falls back to sampling-based SMC methods when exact computations fail. This algorithm thus implements automatic Rao-Blackwellization and is even exact for Gaussian tree models.

Interpretable Meta-Learning of Physical Systems

Machine learning methods can be a valuable aid in the scientific process, but they need to face challenging settings where data come from inhomogeneous experimental conditions. Recent meta-learning methods have made significant progress in multi-task learning, but they rely on black-box neural networks, resulting in high computational costs and limited interpretability. Leveraging the structure of the learning problem, we argue that multi-environment generalization can be achieved using a simpler learning model, with an affine structure with respect to the learning task. Crucially, we prove that this architecture can identify the physical parameters of the system, enabling interpreable learning. We demonstrate the competitive generalization performance and the low computational cost of our method by comparing it to state-of-the-art algorithms on physical systems, ranging from toy models to complex, non-analytical systems. The interpretability of our method is illustrated with original applications to physical-parameter-induced adaptation and to adaptive control.

FLEX: an Adaptive Exploration Algorithm for Nonlinear Systems

Model-based reinforcement learning is a powerful tool, but collecting data to fit an accurate model of the system can be costly. Exploring an unknown environment in a sample-efficient manner is hence of great importance. However, the complexity of dynamics and the computational limitations of real systems make this task challenging. In this work, we introduce FLEX, an exploration algorithm for nonlinear dynamics based on optimal experimental design. Our policy maximizes the information of the next step and results in an adaptive exploration algorithm, compatible with generic parametric learning models and requiring minimal resources. We test our method on a number of nonlinear environments covering different settings, including time-varying dynamics. Keeping in mind that exploration is intended to serve an exploitation objective, we also test our algorithm on downstream model-based classical control tasks and compare it to other state-of-the-art model-based and model-free approaches. The performance achieved by FLEX is competitive and its computational cost is low.

Convergence beyond the over-parameterized regime using Rayleigh quotients

In this paper, we present a new strategy to prove the convergence of deep learning architectures to a zero training (or even testing) loss by gradient flow. Our analysis is centered on the notion of Rayleigh quotients in order to prove Kurdyka-{\L}ojasiewicz inequalities for a broader set of neural network architectures and loss functions. We show that Rayleigh quotients provide a unified view for several convergence analysis techniques in the literature. Our strategy produces a proof of convergence for various examples of parametric learning. In particular, our analysis does not require the number of parameters to tend to infinity, nor the number of samples to be finite, thus extending to test loss minimization and beyond the over-parameterized regime.

Online greedy identification of linear dynamical systems

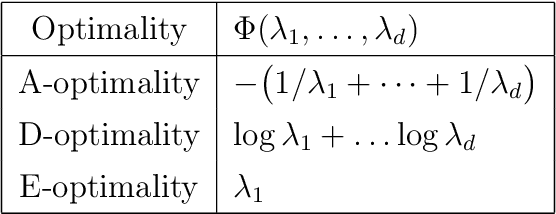
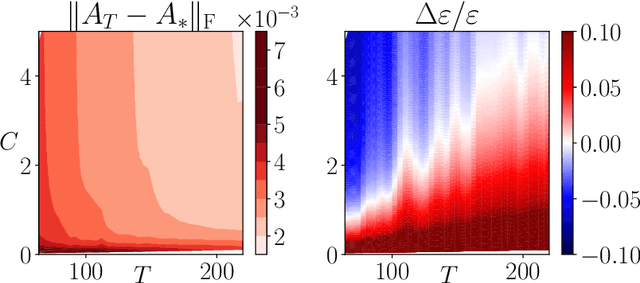
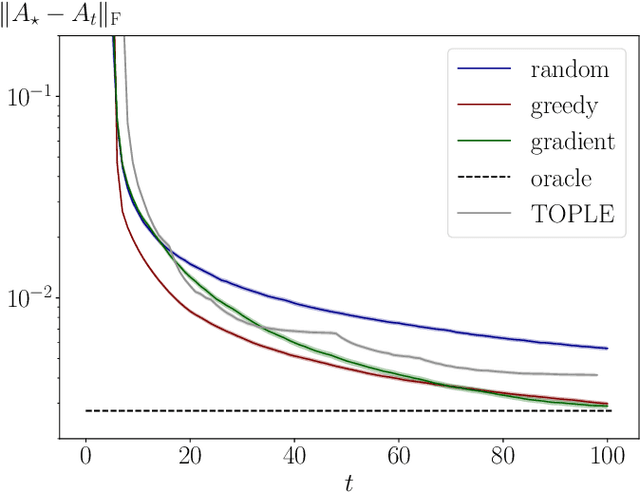
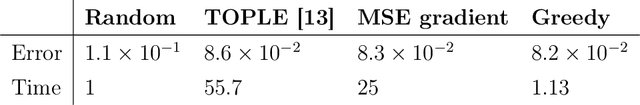
This work addresses the problem of exploration in an unknown environment. For linear dynamical systems, we use an experimental design framework and introduce an online greedy policy where the control maximizes the information of the next step. In a setting with a limited number of experimental trials, our algorithm has low complexity and shows experimentally competitive performances compared to more elaborate gradient-based methods.

SiMCa: Sinkhorn Matrix Factorization with Capacity Constraints

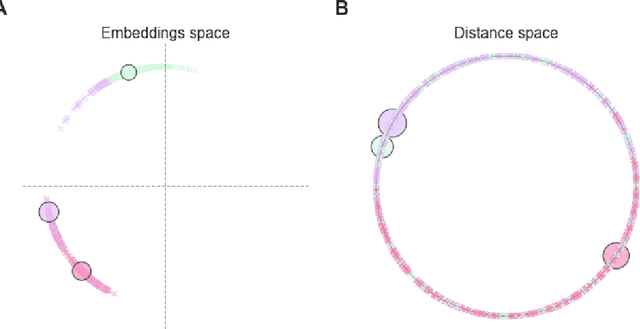
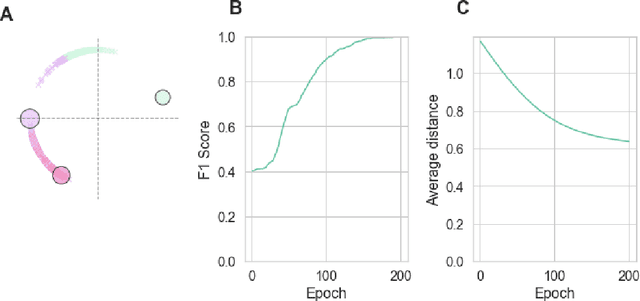
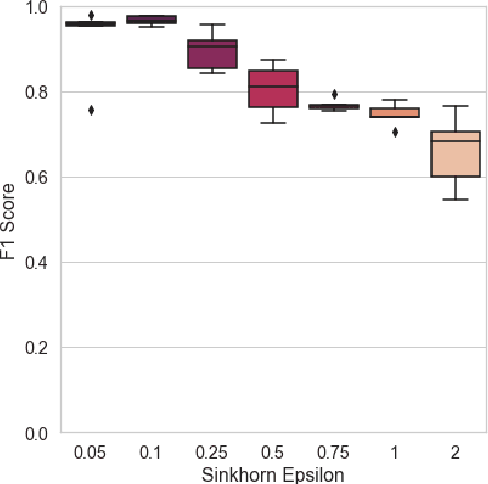
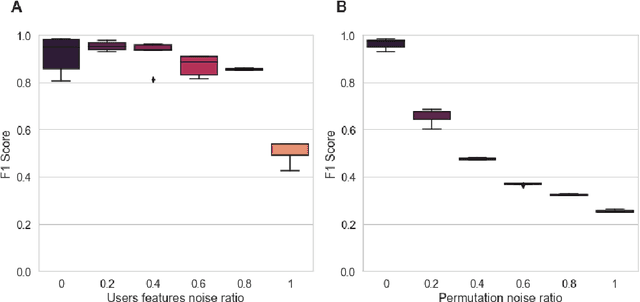
For a very broad range of problems, recommendation algorithms have been increasingly used over the past decade. In most of these algorithms, the predictions are built upon user-item affinity scores which are obtained from high-dimensional embeddings of items and users. In more complex scenarios, with geometrical or capacity constraints, prediction based on embeddings may not be sufficient and some additional features should be considered in the design of the algorithm. In this work, we study the recommendation problem in the setting where affinities between users and items are based both on their embeddings in a latent space and on their geographical distance in their underlying euclidean space (e.g., $\mathbb{R}^2$), together with item capacity constraints. This framework is motivated by some real-world applications, for instance in healthcare: the task is to recommend hospitals to patients based on their location, pathology, and hospital capacities. In these applications, there is somewhat of an asymmetry between users and items: items are viewed as static points, their embeddings, capacities and locations constraining the allocation. Upon the observation of an optimal allocation, user embeddings, items capacities, and their positions in their underlying euclidean space, our aim is to recover item embeddings in the latent space; doing so, we are then able to use this estimate e.g. in order to predict future allocations. We propose an algorithm (SiMCa) based on matrix factorization enhanced with optimal transport steps to model user-item affinities and learn item embeddings from observed data. We then illustrate and discuss the results of such an approach for hospital recommendation on synthetic data.

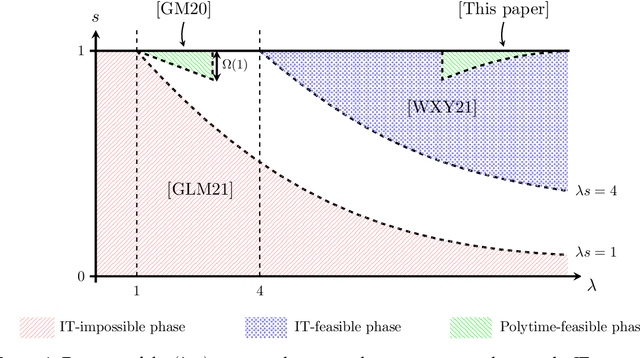
Correlation detection in trees for partial graph alignment

We consider alignment of sparse graphs, which consists in finding a mapping between the nodes of two graphs which preserves most of the edges. Our approach is to compare local structures in the two graphs, matching two nodes if their neighborhoods are 'close enough': for correlated Erd\H{o}s-R\'enyi random graphs, this problem can be locally rephrased in terms of testing whether a pair of branching trees is drawn from either a product distribution, or a correlated distribution. We design an optimal test for this problem which gives rise to a message-passing algorithm for graph alignment, which provably returns in polynomial time a positive fraction of correctly matched vertices, and a vanishing fraction of mismatches. With an average degree $\lambda = O(1)$ in the graphs, and a correlation parameter $s \in [0,1]$, this result holds with $\lambda s$ large enough, and $1-s$ small enough, completing the recent state-of-the-art diagram. Tighter conditions for determining whether partial graph alignment (or correlation detection in trees) is feasible in polynomial time are given in terms of Kullback-Leibler divergences.