Aligning Embeddings and Geometric Random Graphs: Informational Results and Computational Approaches for the Procrustes-Wasserstein Problem

The Procrustes-Wasserstein problem consists in matching two high-dimensional point clouds in an unsupervised setting, and has many applications in natural language processing and computer vision. We consider a planted model with two datasets $X,Y$ that consist of $n$ datapoints in $\mathbb{R}^d$, where $Y$ is a noisy version of $X$, up to an orthogonal transformation and a relabeling of the data points. This setting is related to the graph alignment problem in geometric models. In this work, we focus on the euclidean transport cost between the point clouds as a measure of performance for the alignment. We first establish information-theoretic results, in the high ($d \gg \log n$) and low ($d \ll \log n$) dimensional regimes. We then study computational aspects and propose the Ping-Pong algorithm, alternatively estimating the orthogonal transformation and the relabeling, initialized via a Franke-Wolfe convex relaxation. We give sufficient conditions for the method to retrieve the planted signal after one single step. We provide experimental results to compare the proposed approach with the state-of-the-art method of Grave et al. (2019).

The graph alignment problem: fundamental limits and efficient algorithms

This thesis studies the graph alignment problem, the noisy version of the graph isomorphism problem, which aims to find a matching between the nodes of two graphs which preserves most of the edges. Focusing on the planted version where the graphs are random, we are interested in understanding the fundamental information-theoretical limits for this problem, as well as designing and analyzing algorithms that are able to recover the underlying alignment in the data. For these algorithms, we give some high probability guarantees on the regime in which they succeed or fail.

On sample complexity of conditional independence testing with Von Mises estimator with application to causal discovery

Motivated by conditional independence testing, an essential step in constraint-based causal discovery algorithms, we study the nonparametric Von Mises estimator for the entropy of multivariate distributions built on a kernel density estimator. We establish an exponential concentration inequality for this estimator. We design a test for conditional independence (CI) based on our estimator, called VM-CI, which achieves optimal parametric rates under smoothness assumptions. Leveraging the exponential concentration, we prove a tight upper bound for the overall error of VM-CI. This, in turn, allows us to characterize the sample complexity of any constraint-based causal discovery algorithm that uses VM-CI for CI tests. To the best of our knowledge, this is the first sample complexity guarantee for causal discovery for continuous variables. Furthermore, we empirically show that VM-CI outperforms other popular CI tests in terms of either time or sample complexity (or both), which translates to a better performance in structure learning as well.

Learning Causal Graphs via Monotone Triangular Transport Maps

We study the problem of causal structure learning from data using optimal transport (OT). Specifically, we first provide a constraint-based method which builds upon lower-triangular monotone parametric transport maps to design conditional independence tests which are agnostic to the noise distribution. We provide an algorithm for causal discovery up to Markov Equivalence with no assumptions on the structural equations/noise distributions, which allows for settings with latent variables. Our approach also extends to score-based causal discovery by providing a novel means for defining scores. This allows us to uniquely recover the causal graph under additional identifiability and structural assumptions, such as additive noise or post-nonlinear models. We provide experimental results to compare the proposed approach with the state of the art on both synthetic and real-world datasets.

Statistical limits of correlation detection in trees

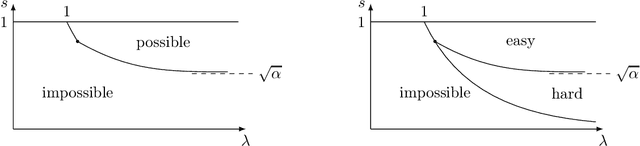
In this paper we address the problem of testing whether two observed trees $(t,t')$ are sampled either independently or from a joint distribution under which they are correlated. This problem, which we refer to as correlation detection in trees, plays a key role in the study of graph alignment for two correlated random graphs. Motivated by graph alignment, we investigate the conditions of existence of one-sided tests, i.e. tests which have vanishing type I error and non-vanishing power in the limit of large tree depth. For the correlated Galton-Watson model with Poisson offspring of mean $\lambda>0$ and correlation parameter $s \in (0,1)$, we identify a phase transition in the limit of large degrees at $s = \sqrt{\alpha}$, where $\alpha \sim 0.3383$ is Otter's constant. Namely, we prove that no such test exists for $s \leq \sqrt{\alpha}$, and that such a test exists whenever $s > \sqrt{\alpha}$, for $\lambda$ large enough. This result sheds new light on the graph alignment problem in the sparse regime (with $O(1)$ average node degrees) and on the performance of the MPAlign method studied in Ganassali et al. (2021), Piccioli et al. (2021), proving in particular the conjecture of Piccioli et al. (2021) that MPAlign succeeds in the partial recovery task for correlation parameter $s>\sqrt{\alpha}$ provided the average node degree $\lambda$ is large enough.

SiMCa: Sinkhorn Matrix Factorization with Capacity Constraints

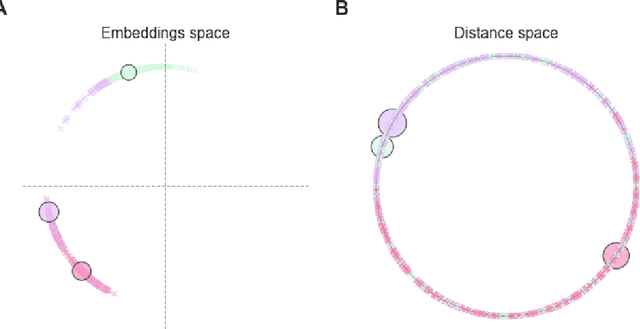
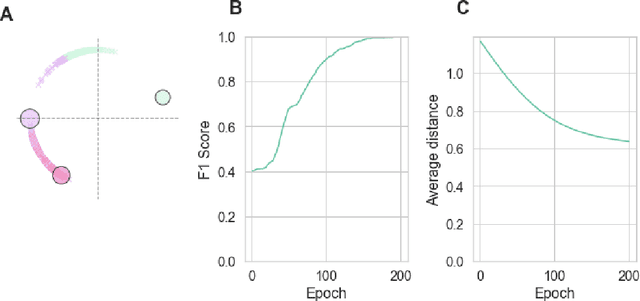
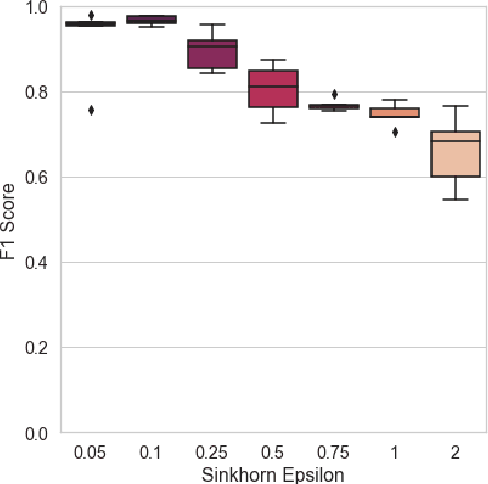
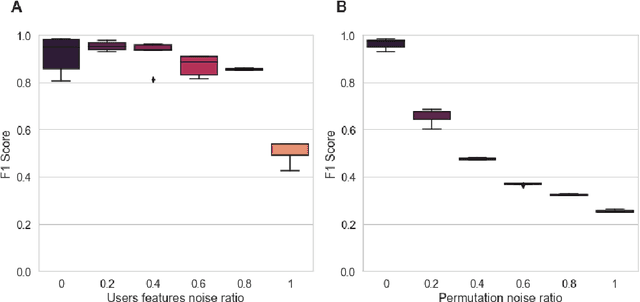
For a very broad range of problems, recommendation algorithms have been increasingly used over the past decade. In most of these algorithms, the predictions are built upon user-item affinity scores which are obtained from high-dimensional embeddings of items and users. In more complex scenarios, with geometrical or capacity constraints, prediction based on embeddings may not be sufficient and some additional features should be considered in the design of the algorithm. In this work, we study the recommendation problem in the setting where affinities between users and items are based both on their embeddings in a latent space and on their geographical distance in their underlying euclidean space (e.g., $\mathbb{R}^2$), together with item capacity constraints. This framework is motivated by some real-world applications, for instance in healthcare: the task is to recommend hospitals to patients based on their location, pathology, and hospital capacities. In these applications, there is somewhat of an asymmetry between users and items: items are viewed as static points, their embeddings, capacities and locations constraining the allocation. Upon the observation of an optimal allocation, user embeddings, items capacities, and their positions in their underlying euclidean space, our aim is to recover item embeddings in the latent space; doing so, we are then able to use this estimate e.g. in order to predict future allocations. We propose an algorithm (SiMCa) based on matrix factorization enhanced with optimal transport steps to model user-item affinities and learn item embeddings from observed data. We then illustrate and discuss the results of such an approach for hospital recommendation on synthetic data.

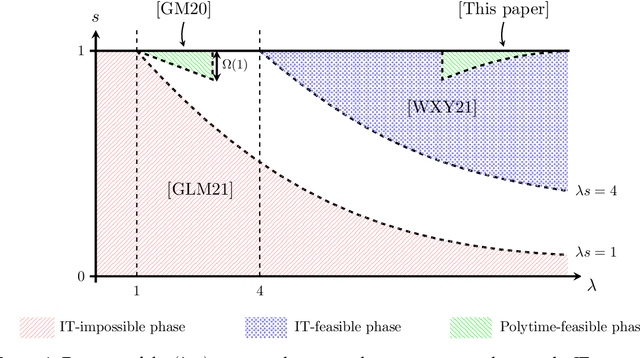
Correlation detection in trees for partial graph alignment

We consider alignment of sparse graphs, which consists in finding a mapping between the nodes of two graphs which preserves most of the edges. Our approach is to compare local structures in the two graphs, matching two nodes if their neighborhoods are 'close enough': for correlated Erd\H{o}s-R\'enyi random graphs, this problem can be locally rephrased in terms of testing whether a pair of branching trees is drawn from either a product distribution, or a correlated distribution. We design an optimal test for this problem which gives rise to a message-passing algorithm for graph alignment, which provably returns in polynomial time a positive fraction of correctly matched vertices, and a vanishing fraction of mismatches. With an average degree $\lambda = O(1)$ in the graphs, and a correlation parameter $s \in [0,1]$, this result holds with $\lambda s$ large enough, and $1-s$ small enough, completing the recent state-of-the-art diagram. Tighter conditions for determining whether partial graph alignment (or correlation detection in trees) is feasible in polynomial time are given in terms of Kullback-Leibler divergences.

Impossibility of Partial Recovery in the Graph Alignment Problem

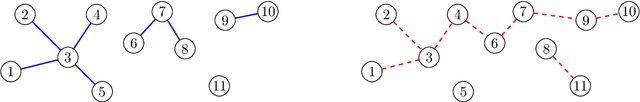
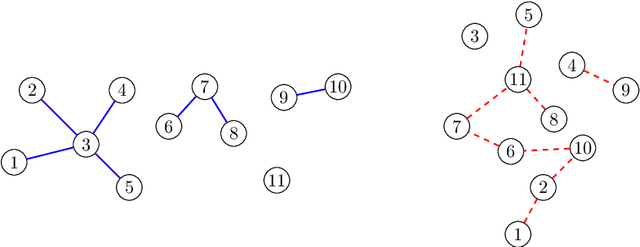
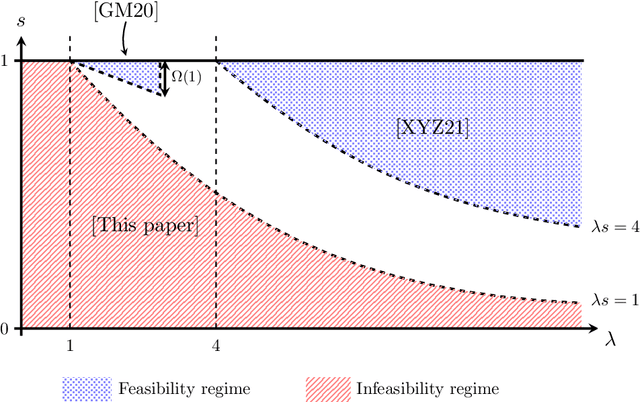
Random graph alignment refers to recovering the underlying vertex correspondence between two random graphs with correlated edges. This can be viewed as an average-case and noisy version of the well-known NP-hard graph isomorphism problem. For the correlated Erd\"os-R\'enyi model, we prove an impossibility result for partial recovery in the sparse regime, with constant average degree and correlation, as well as a general bound on the maximal reachable overlap. Our bound is tight in the noiseless case (the graph isomorphism problem) and we conjecture that it is still tight with noise. Our proof technique relies on a careful application of the probabilistic method to build automorphisms between tree components of a subcritical Erd\"os-R\'enyi graph.

Sharp threshold for alignment of graph databases with Gaussian weights

We study the fundamental limits for reconstruction in weighted graph (or matrix) database alignment. We consider a model of two graphs where $\pi^*$ is a planted uniform permutation and all pairs of edge weights $(A_{i,j}, B_{\pi^*(i),\pi^*(j)})_{1 \leq i<j \leq n}$ are i.i.d. pairs of Gaussian variables with zero mean, unit variance and correlation parameter $\rho \in [0,1]$. We prove that there is a sharp threshold for exact recovery of $\pi^*$: if $n \rho^2 \geq (4+\varepsilon) \log n + \omega(1)$ for some $\varepsilon>0$, there is an estimator $\hat{\pi}$ -- namely the MAP estimator -- based on the observation of databases $A,B$ that achieves exact reconstruction with high probability. Conversely, if $n \rho^2 \leq 4 \log n - \log \log n - \omega(1)$, then any estimator $\hat{\pi}$ verifies $\hat{\pi}=\pi$ with probability $o(1)$. This result shows that the information-theoretic threshold for exact recovery is the same as the one obtained for detection in a recent work by Y. Wu, J. Xu and S. Yu: in other words, for Gaussian weighted graph alignment, the problem of reconstruction is not more difficult than that of detection. Though the reconstruction task was already well understood for vector-shaped database alignment (that is taking signal of the form $(u_i, v_{\pi^*(i)})_{1 \leq i\leq n}$ where $(u_i, v_{\pi^*(i)})$ are i.i.d. pairs in $\mathbb{R}^{d_u} \times \mathbb{R}^{d_v}$), its formulation for graph (or matrix) databases brings a drastically different problem for which the hard phase is conjectured to be huge. The study is based on the analysis of the MAP estimator, and proofs rely on proper use of the correlation structure of energies of permutations.