In-depth Analysis of Low-rank Matrix Factorisation in a Federated Setting

We analyze a distributed algorithm to compute a low-rank matrix factorization on $N$ clients, each holding a local dataset $\mathbf{S}^i \in \mathbb{R}^{n_i \times d}$, mathematically, we seek to solve $min_{\mathbf{U}^i \in \mathbb{R}^{n_i\times r}, \mathbf{V}\in \mathbb{R}^{d \times r} } \frac{1}{2} \sum_{i=1}^N \|\mathbf{S}^i - \mathbf{U}^i \mathbf{V}^\top\|^2_{\text{F}}$. Considering a power initialization of $\mathbf{V}$, we rewrite the previous smooth non-convex problem into a smooth strongly-convex problem that we solve using a parallel Nesterov gradient descent potentially requiring a single step of communication at the initialization step. For any client $i$ in $\{1, \dots, N\}$, we obtain a global $\mathbf{V}$ in $\mathbb{R}^{d \times r}$ common to all clients and a local variable $\mathbf{U}^i$ in $\mathbb{R}^{n_i \times r}$. We provide a linear rate of convergence of the excess loss which depends on $\sigma_{\max} / \sigma_{r}$, where $\sigma_{r}$ is the $r^{\mathrm{th}}$ singular value of the concatenation $\mathbf{S}$ of the matrices $(\mathbf{S}^i)_{i=1}^N$. This result improves the rates of convergence given in the literature, which depend on $\sigma_{\max}^2 / \sigma_{\min}^2$. We provide an upper bound on the Frobenius-norm error of reconstruction under the power initialization strategy. We complete our analysis with experiments on both synthetic and real data.

Generalization Error of First-Order Methods for Statistical Learning with Generic Oracles

In this paper, we provide a novel framework for the analysis of generalization error of first-order optimization algorithms for statistical learning when the gradient can only be accessed through partial observations given by an oracle. Our analysis relies on the regularity of the gradient w.r.t. the data samples, and allows to derive near matching upper and lower bounds for the generalization error of multiple learning problems, including supervised learning, transfer learning, robust learning, distributed learning and communication efficient learning using gradient quantization. These results hold for smooth and strongly-convex optimization problems, as well as smooth non-convex optimization problems verifying a Polyak-Lojasiewicz assumption. In particular, our upper and lower bounds depend on a novel quantity that extends the notion of conditional standard deviation, and is a measure of the extent to which the gradient can be approximated by having access to the oracle. As a consequence, our analysis provides a precise meaning to the intuition that optimization of the statistical learning objective is as hard as the estimation of its gradient. Finally, we show that, in the case of standard supervised learning, mini-batch gradient descent with increasing batch sizes and a warm start can reach a generalization error that is optimal up to a multiplicative factor, thus motivating the use of this optimization scheme in practical applications.

Convergence beyond the over-parameterized regime using Rayleigh quotients

In this paper, we present a new strategy to prove the convergence of deep learning architectures to a zero training (or even testing) loss by gradient flow. Our analysis is centered on the notion of Rayleigh quotients in order to prove Kurdyka-{\L}ojasiewicz inequalities for a broader set of neural network architectures and loss functions. We show that Rayleigh quotients provide a unified view for several convergence analysis techniques in the literature. Our strategy produces a proof of convergence for various examples of parametric learning. In particular, our analysis does not require the number of parameters to tend to infinity, nor the number of samples to be finite, thus extending to test loss minimization and beyond the over-parameterized regime.

Tight High Probability Bounds for Linear Stochastic Approximation with Fixed Stepsize

This paper provides a non-asymptotic analysis of linear stochastic approximation (LSA) algorithms with fixed stepsize. This family of methods arises in many machine learning tasks and is used to obtain approximate solutions of a linear system $\bar{A}\theta = \bar{b}$ for which $\bar{A}$ and $\bar{b}$ can only be accessed through random estimates $\{({\bf A}_n, {\bf b}_n): n \in \mathbb{N}^*\}$. Our analysis is based on new results regarding moments and high probability bounds for products of matrices which are shown to be tight. We derive high probability bounds on the performance of LSA under weaker conditions on the sequence $\{({\bf A}_n, {\bf b}_n): n \in \mathbb{N}^*\}$ than previous works. However, in contrast, we establish polynomial concentration bounds with order depending on the stepsize. We show that our conclusions cannot be improved without additional assumptions on the sequence of random matrices $\{{\bf A}_n: n \in \mathbb{N}^*\}$, and in particular that no Gaussian or exponential high probability bounds can hold. Finally, we pay a particular attention to establishing bounds with sharp order with respect to the number of iterations and the stepsize and whose leading terms contain the covariance matrices appearing in the central limit theorems.

Lipschitz Normalization for Self-Attention Layers with Application to Graph Neural Networks

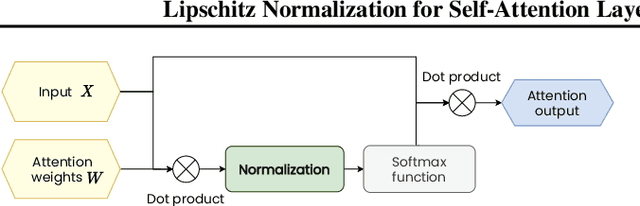
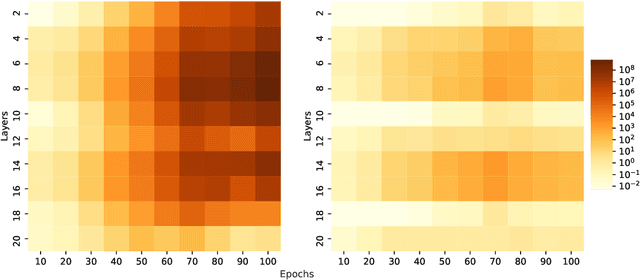
Attention based neural networks are state of the art in a large range of applications. However, their performance tends to degrade when the number of layers increases. In this work, we show that enforcing Lipschitz continuity by normalizing the attention scores can significantly improve the performance of deep attention models. First, we show that, for deep graph attention networks (GAT), gradient explosion appears during training, leading to poor performance of gradient-based training algorithms. To address this issue, we derive a theoretical analysis of the Lipschitz continuity of attention modules and introduce LipschitzNorm, a simple and parameter-free normalization for self-attention mechanisms that enforces the model to be Lipschitz continuous. We then apply LipschitzNorm to GAT and Graph Transformers and show that their performance is substantially improved in the deep setting (10 to 30 layers). More specifically, we show that a deep GAT model with LipschitzNorm achieves state of the art results for node label prediction tasks that exhibit long-range dependencies, while showing consistent improvements over their unnormalized counterparts in benchmark node classification tasks.

Improving Hierarchical Adversarial Robustness of Deep Neural Networks

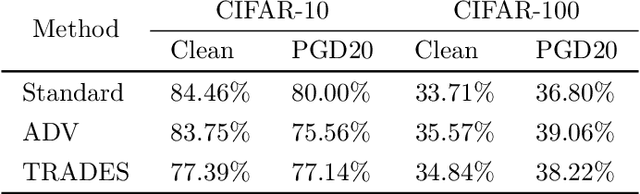
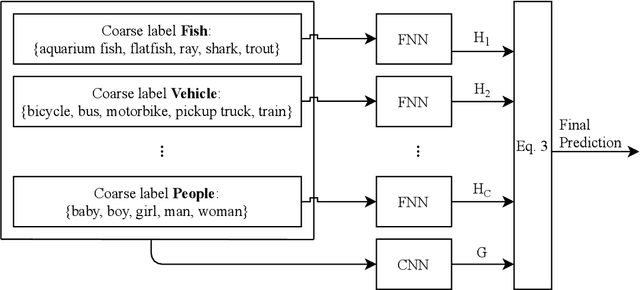
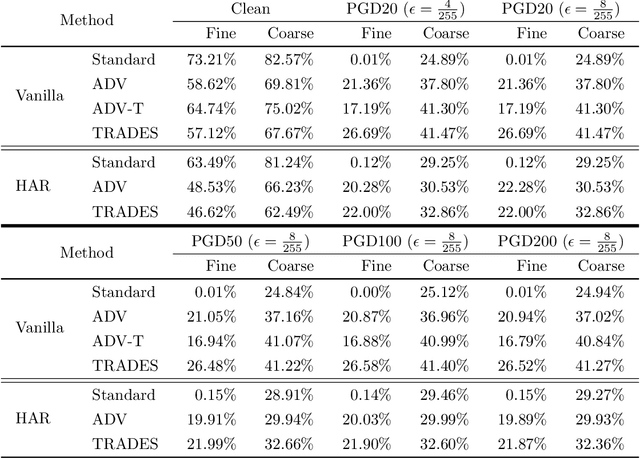
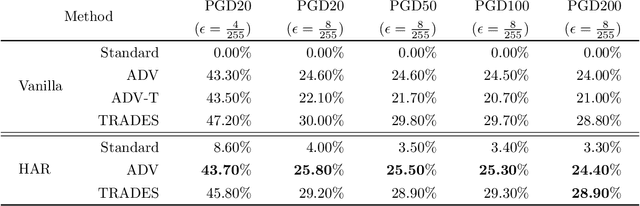
Do all adversarial examples have the same consequences? An autonomous driving system misclassifying a pedestrian as a car may induce a far more dangerous -- and even potentially lethal -- behavior than, for instance, a car as a bus. In order to better tackle this important problematic, we introduce the concept of hierarchical adversarial robustness. Given a dataset whose classes can be grouped into coarse-level labels, we define hierarchical adversarial examples as the ones leading to a misclassification at the coarse level. To improve the resistance of neural networks to hierarchical attacks, we introduce a hierarchical adversarially robust (HAR) network design that decomposes a single classification task into one coarse and multiple fine classification tasks, before being specifically trained by adversarial defense techniques. As an alternative to an end-to-end learning approach, we show that HAR significantly improves the robustness of the network against $\ell_2$ and $\ell_{\infty}$ bounded hierarchical attacks on the CIFAR-10 and CIFAR-100 dataset.

Ego-based Entropy Measures for Structural Representations on Graphs

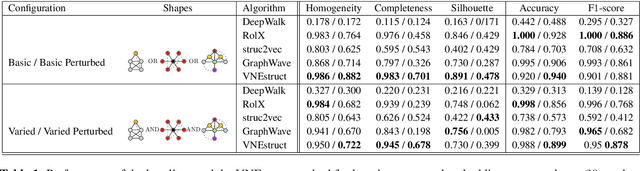
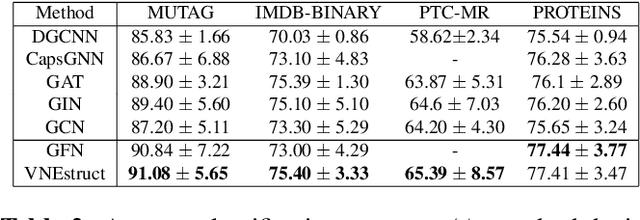
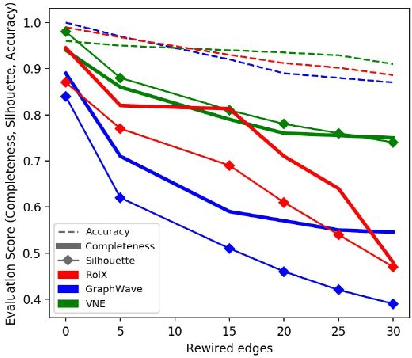
Machine learning on graph-structured data has attracted high research interest due to the emergence of Graph Neural Networks (GNNs). Most of the proposed GNNs are based on the node homophily, i.e neighboring nodes share similar characteristics. However, in many complex networks, nodes that lie to distant parts of the graph share structurally equivalent characteristics and exhibit similar roles (e.g chemical properties of distant atoms in a molecule, type of social network users). A growing literature proposed representations that identify structurally equivalent nodes. However, most of the existing methods require high time and space complexity. In this paper, we propose VNEstruct, a simple approach, based on entropy measures of the neighborhood's topology, for generating low-dimensional structural representations, that is time-efficient and robust to graph perturbations. Empirically, we observe that VNEstruct exhibits robustness on structural role identification tasks. Moreover, VNEstruct can achieve state-of-the-art performance on graph classification, without incorporating the graph structure information in the optimization, in contrast to GNN competitors.

Ego-based Entropy Measures for Structural Representations

In complex networks, nodes that share similar structural characteristics often exhibit similar roles (e.g type of users in a social network or the hierarchical position of employees in a company). In order to leverage this relationship, a growing literature proposed latent representations that identify structurally equivalent nodes. However, most of the existing methods require high time and space complexity. In this paper, we propose VNEstruct, a simple approach for generating low-dimensional structural node embeddings, that is both time efficient and robust to perturbations of the graph structure. The proposed approach focuses on the local neighborhood of each node and employs the Von Neumann entropy, an information-theoretic tool, to extract features that capture the neighborhood's topology. Moreover, on graph classification tasks, we suggest the utilization of the generated structural embeddings for the transformation of an attributed graph structure into a set of augmented node attributes. Empirically, we observe that the proposed approach exhibits robustness on structural role identification tasks and state-of-the-art performance on graph classification tasks, while maintaining very high computational speed.

Coloring graph neural networks for node disambiguation

In this paper, we show that a simple coloring scheme can improve, both theoretically and empirically, the expressive power of Message Passing Neural Networks(MPNNs). More specifically, we introduce a graph neural network called Colored Local Iterative Procedure (CLIP) that uses colors to disambiguate identical node attributes, and show that this representation is a universal approximator of continuous functions on graphs with node attributes. Our method relies on separability , a key topological characteristic that allows to extend well-chosen neural networks into universal representations. Finally, we show experimentally that CLIP is capable of capturing structural characteristics that traditional MPNNs fail to distinguish,while being state-of-the-art on benchmark graph classification datasets.

Theoretical Limits of Pipeline Parallel Optimization and Application to Distributed Deep Learning

We investigate the theoretical limits of pipeline parallel learning of deep learning architectures, a distributed setup in which the computation is distributed per layer instead of per example. For smooth convex and non-convex objective functions, we provide matching lower and upper complexity bounds and show that a naive pipeline parallelization of Nesterov's accelerated gradient descent is optimal. For non-smooth convex functions, we provide a novel algorithm coined Pipeline Parallel Random Smoothing (PPRS) that is within a $d^{1/4}$ multiplicative factor of the optimal convergence rate, where $d$ is the underlying dimension. While the convergence rate still obeys a slow $\varepsilon^{-2}$ convergence rate, the depth-dependent part is accelerated, resulting in a near-linear speed-up and convergence time that only slightly depends on the depth of the deep learning architecture. Finally, we perform an empirical analysis of the non-smooth non-convex case and show that, for difficult and highly non-smooth problems, PPRS outperforms more traditional optimization algorithms such as gradient descent and Nesterov's accelerated gradient descent for problems where the sample size is limited, such as few-shot or adversarial learning.