Proximal optimal transport divergences

We introduce proximal optimal transport divergence, a novel discrepancy measure that interpolates between information divergences and optimal transport distances via an infimal convolution formulation. This divergence provides a principled foundation for optimal transport proximals and proximal optimization methods frequently used in generative modeling. We explore its mathematical properties, including smoothness, boundedness, and computational tractability, and establish connections to primal-dual formulation and adversarial learning. Building on the Benamou-Brenier dynamic formulation of optimal transport cost, we also establish a dynamic formulation for proximal OT divergences. The resulting dynamic formulation is a first order mean-field game whose optimality conditions are governed by a pair of nonlinear partial differential equations, a backward Hamilton-Jacobi and a forward continuity partial differential equations. Our framework generalizes existing approaches while offering new insights and computational tools for generative modeling, distributional optimization, and gradient-based learning in probability spaces.

Combining Wasserstein-1 and Wasserstein-2 proximals: robust manifold learning via well-posed generative flows

We formulate well-posed continuous-time generative flows for learning distributions that are supported on low-dimensional manifolds through Wasserstein proximal regularizations of $f$-divergences. Wasserstein-1 proximal operators regularize $f$-divergences so that singular distributions can be compared. Meanwhile, Wasserstein-2 proximal operators regularize the paths of the generative flows by adding an optimal transport cost, i.e., a kinetic energy penalization. Via mean-field game theory, we show that the combination of the two proximals is critical for formulating well-posed generative flows. Generative flows can be analyzed through optimality conditions of a mean-field game (MFG), a system of a backward Hamilton-Jacobi (HJ) and a forward continuity partial differential equations (PDEs) whose solution characterizes the optimal generative flow. For learning distributions that are supported on low-dimensional manifolds, the MFG theory shows that the Wasserstein-1 proximal, which addresses the HJ terminal condition, and the Wasserstein-2 proximal, which addresses the HJ dynamics, are both necessary for the corresponding backward-forward PDE system to be well-defined and have a unique solution with provably linear flow trajectories. This implies that the corresponding generative flow is also unique and can therefore be learned in a robust manner even for learning high-dimensional distributions supported on low-dimensional manifolds. The generative flows are learned through adversarial training of continuous-time flows, which bypasses the need for reverse simulation. We demonstrate the efficacy of our approach for generating high-dimensional images without the need to resort to autoencoders or specialized architectures.

Nonlinear denoising score matching for enhanced learning of structured distributions

We present a novel method for training score-based generative models which uses nonlinear noising dynamics to improve learning of structured distributions. Generalizing to a nonlinear drift allows for additional structure to be incorporated into the dynamics, thus making the training better adapted to the data, e.g., in the case of multimodality or (approximate) symmetries. Such structure can be obtained from the data by an inexpensive preprocessing step. The nonlinear dynamics introduces new challenges into training which we address in two ways: 1) we develop a new nonlinear denoising score matching (NDSM) method, 2) we introduce neural control variates in order to reduce the variance of the NDSM training objective. We demonstrate the effectiveness of this method on several examples: a) a collection of low-dimensional examples, motivated by clustering in latent space, b) high-dimensional images, addressing issues with mode collapse, small training sets, and approximate symmetries, the latter being a challenge for methods based on equivariant neural networks, which require exact symmetries.

Learning heavy-tailed distributions with Wasserstein-proximal-regularized $α$-divergences

In this paper, we propose Wasserstein proximals of $\alpha$-divergences as suitable objective functionals for learning heavy-tailed distributions in a stable manner. First, we provide sufficient, and in some cases necessary, relations among data dimension, $\alpha$, and the decay rate of data distributions for the Wasserstein-proximal-regularized divergence to be finite. Finite-sample convergence rates for the estimation in the case of the Wasserstein-1 proximal divergences are then provided under certain tail conditions. Numerical experiments demonstrate stable learning of heavy-tailed distributions -- even those without first or second moment -- without any explicit knowledge of the tail behavior, using suitable generative models such as GANs and flow-based models related to our proposed Wasserstein-proximal-regularized $\alpha$-divergences. Heuristically, $\alpha$-divergences handle the heavy tails and Wasserstein proximals allow non-absolute continuity between distributions and control the velocities of flow-based algorithms as they learn the target distribution deep into the tails.

Statistical Guarantees of Group-Invariant GANs

Group-invariant generative adversarial networks (GANs) are a type of GANs in which the generators and discriminators are hardwired with group symmetries. Empirical studies have shown that these networks are capable of learning group-invariant distributions with significantly improved data efficiency. In this study, we aim to rigorously quantify this improvement by analyzing the reduction in sample complexity for group-invariant GANs. Our findings indicate that when learning group-invariant distributions, the number of samples required for group-invariant GANs decreases proportionally with a power of the group size, and this power depends on the intrinsic dimension of the distribution's support. To our knowledge, this work presents the first statistical estimation for group-invariant generative models, specifically for GANs, and it may shed light on the study of other group-invariant generative models.

Sample Complexity of Probability Divergences under Group Symmetry

We rigorously quantify the improvement in the sample complexity of variational divergence estimations for group-invariant distributions. In the cases of the Wasserstein-1 metric and the Lipschitz-regularized $\alpha$-divergences, the reduction of sample complexity is proportional to an ambient-dimension-dependent power of the group size. For the maximum mean discrepancy (MMD), the improvement of sample complexity is more nuanced, as it depends on not only the group size but also the choice of kernel. Numerical simulations verify our theories.

Lipschitz regularized gradient flows and latent generative particles

Lipschitz regularized f-divergences are constructed by imposing a bound on the Lipschitz constant of the discriminator in the variational representation. They interpolate between the Wasserstein metric and f-divergences and provide a flexible family of loss functions for non-absolutely continuous (e.g. empirical) distributions, possibly with heavy tails. We construct Lipschitz regularized gradient flows on the space of probability measures based on these divergences. Examples of such gradient flows are Lipschitz regularized Fokker-Planck and porous medium partial differential equations (PDEs) for the Kullback-Leibler and alpha-divergences, respectively. The regularization corresponds to imposing a Courant-Friedrichs-Lewy numerical stability condition on the PDEs. For empirical measures, the Lipschitz regularization on gradient flows induces a numerically stable transporter/discriminator particle algorithm, where the generative particles are transported along the gradient of the discriminator. The gradient structure leads to a regularized Fisher information (particle kinetic energy) used to track the convergence of the algorithm. The Lipschitz regularized discriminator can be implemented via neural network spectral normalization and the particle algorithm generates approximate samples from possibly high-dimensional distributions known only from data. Notably, our particle algorithm can generate synthetic data even in small sample size regimes. A new data processing inequality for the regularized divergence allows us to combine our particle algorithm with representation learning, e.g. autoencoder architectures. The resulting algorithm yields markedly improved generative properties in terms of efficiency and quality of the synthetic samples. From a statistical mechanics perspective the encoding can be interpreted dynamically as learning a better mobility for the generative particles.

Function-space regularized Rényi divergences

We propose a new family of regularized R\'enyi divergences parametrized not only by the order $\alpha$ but also by a variational function space. These new objects are defined by taking the infimal convolution of the standard R\'enyi divergence with the integral probability metric (IPM) associated with the chosen function space. We derive a novel dual variational representation that can be used to construct numerically tractable divergence estimators. This representation avoids risk-sensitive terms and therefore exhibits lower variance, making it well-behaved when $\alpha>1$; this addresses a notable weakness of prior approaches. We prove several properties of these new divergences, showing that they interpolate between the classical R\'enyi divergences and IPMs. We also study the $\alpha\to\infty$ limit, which leads to a regularized worst-case-regret and a new variational representation in the classical case. Moreover, we show that the proposed regularized R\'enyi divergences inherit features from IPMs such as the ability to compare distributions that are not absolutely continuous, e.g., empirical measures and distributions with low-dimensional support. We present numerical results on both synthetic and real datasets, showing the utility of these new divergences in both estimation and GAN training applications; in particular, we demonstrate significantly reduced variance and improved training performance.

Structure-preserving GANs

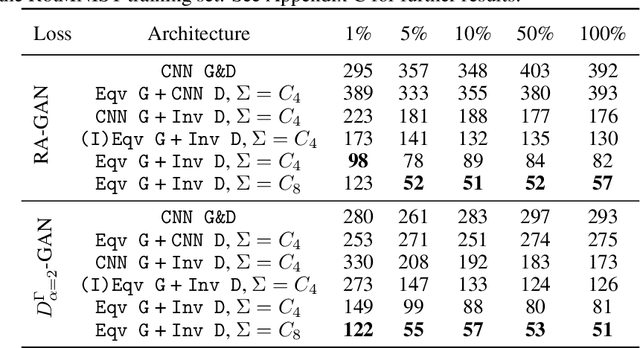
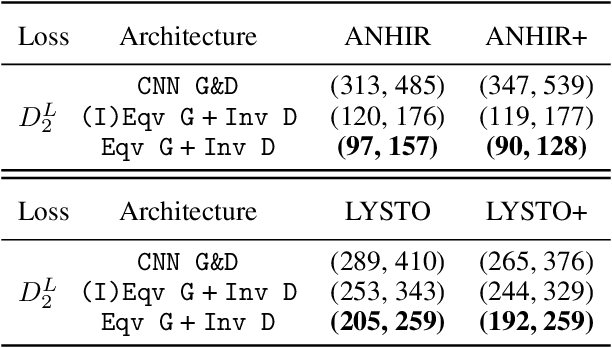
Generative adversarial networks (GANs), a class of distribution-learning methods based on a two-player game between a generator and a discriminator, can generally be formulated as a minmax problem based on the variational representation of a divergence between the unknown and the generated distributions. We introduce structure-preserving GANs as a data-efficient framework for learning distributions with additional structure such as group symmetry, by developing new variational representations for divergences. Our theory shows that we can reduce the discriminator space to its projection on the invariant discriminator space, using the conditional expectation with respect to the $\sigma$-algebra associated to the underlying structure. In addition, we prove that the discriminator space reduction must be accompanied by a careful design of structured generators, as flawed designs may easily lead to a catastrophic "mode collapse" of the learned distribution. We contextualize our framework by building symmetry-preserving GANs for distributions with intrinsic group symmetry, and demonstrate that both players, namely the equivariant generator and invariant discriminator, play important but distinct roles in the learning process. Empirical experiments and ablation studies across a broad range of data sets, including real-world medical imaging, validate our theory, and show our proposed methods achieve significantly improved sample fidelity and diversity -- almost an order of magnitude measured in Fr\'echet Inception Distance -- especially in the small data regime.

Model Uncertainty and Correctability for Directed Graphical Models

Probabilistic graphical models are a fundamental tool in probabilistic modeling, machine learning and artificial intelligence. They allow us to integrate in a natural way expert knowledge, physical modeling, heterogeneous and correlated data and quantities of interest. For exactly this reason, multiple sources of model uncertainty are inherent within the modular structure of the graphical model. In this paper we develop information-theoretic, robust uncertainty quantification methods and non-parametric stress tests for directed graphical models to assess the effect and the propagation through the graph of multi-sourced model uncertainties to quantities of interest. These methods allow us to rank the different sources of uncertainty and correct the graphical model by targeting its most impactful components with respect to the quantities of interest. Thus, from a machine learning perspective, we provide a mathematically rigorous approach to correctability that guarantees a systematic selection for improvement of components of a graphical model while controlling potential new errors created in the process in other parts of the model. We demonstrate our methods in two physico-chemical examples, namely quantum scale-informed chemical kinetics and materials screening to improve the efficiency of fuel cells.