Lipschitz regularized gradient flows and latent generative particles

Lipschitz regularized f-divergences are constructed by imposing a bound on the Lipschitz constant of the discriminator in the variational representation. They interpolate between the Wasserstein metric and f-divergences and provide a flexible family of loss functions for non-absolutely continuous (e.g. empirical) distributions, possibly with heavy tails. We construct Lipschitz regularized gradient flows on the space of probability measures based on these divergences. Examples of such gradient flows are Lipschitz regularized Fokker-Planck and porous medium partial differential equations (PDEs) for the Kullback-Leibler and alpha-divergences, respectively. The regularization corresponds to imposing a Courant-Friedrichs-Lewy numerical stability condition on the PDEs. For empirical measures, the Lipschitz regularization on gradient flows induces a numerically stable transporter/discriminator particle algorithm, where the generative particles are transported along the gradient of the discriminator. The gradient structure leads to a regularized Fisher information (particle kinetic energy) used to track the convergence of the algorithm. The Lipschitz regularized discriminator can be implemented via neural network spectral normalization and the particle algorithm generates approximate samples from possibly high-dimensional distributions known only from data. Notably, our particle algorithm can generate synthetic data even in small sample size regimes. A new data processing inequality for the regularized divergence allows us to combine our particle algorithm with representation learning, e.g. autoencoder architectures. The resulting algorithm yields markedly improved generative properties in terms of efficiency and quality of the synthetic samples. From a statistical mechanics perspective the encoding can be interpreted dynamically as learning a better mobility for the generative particles.

Model Uncertainty and Correctability for Directed Graphical Models

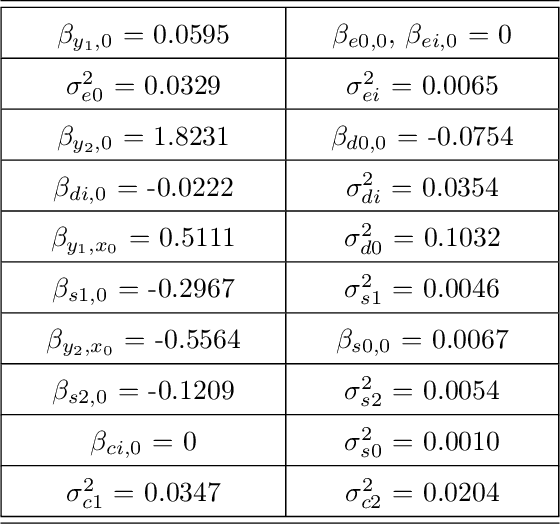
Probabilistic graphical models are a fundamental tool in probabilistic modeling, machine learning and artificial intelligence. They allow us to integrate in a natural way expert knowledge, physical modeling, heterogeneous and correlated data and quantities of interest. For exactly this reason, multiple sources of model uncertainty are inherent within the modular structure of the graphical model. In this paper we develop information-theoretic, robust uncertainty quantification methods and non-parametric stress tests for directed graphical models to assess the effect and the propagation through the graph of multi-sourced model uncertainties to quantities of interest. These methods allow us to rank the different sources of uncertainty and correct the graphical model by targeting its most impactful components with respect to the quantities of interest. Thus, from a machine learning perspective, we provide a mathematically rigorous approach to correctability that guarantees a systematic selection for improvement of components of a graphical model while controlling potential new errors created in the process in other parts of the model. We demonstrate our methods in two physico-chemical examples, namely quantum scale-informed chemical kinetics and materials screening to improve the efficiency of fuel cells.

Uncertainty quantification for Markov Random Fields

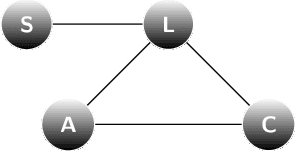
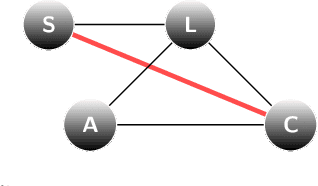
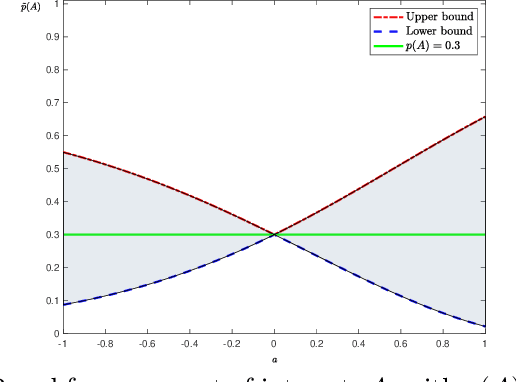
We present an information-based uncertainty quantification method for general Markov Random Fields. Markov Random Fields (MRF) are structured, probabilistic graphical models over undirected graphs, and provide a fundamental unifying modeling tool for statistical mechanics, probabilistic machine learning, and artificial intelligence. Typically MRFs are complex and high-dimensional with nodes and edges (connections) built in a modular fashion from simpler, low-dimensional probabilistic models and their local connections; in turn, this modularity allows to incorporate available data to MRFs and efficiently simulate them by leveraging their graph-theoretic structure. Learning graphical models from data and/or constructing them from physical modeling and constraints necessarily involves uncertainties inherited from data, modeling choices, or numerical approximations. These uncertainties in the MRF can be manifested either in the graph structure or the probability distribution functions, and necessarily will propagate in predictions for quantities of interest. Here we quantify such uncertainties using tight, information based bounds on the predictions of quantities of interest; these bounds take advantage of the graphical structure of MRFs and are capable of handling the inherent high-dimensionality of such graphical models. We demonstrate our methods in MRFs for medical diagnostics and statistical mechanics models. In the latter, we develop uncertainty quantification bounds for finite size effects and phase diagrams, which constitute two of the typical predictions goals of statistical mechanics modeling.