Matrix Completion Via Reweighted Logarithmic Norm Minimization

Low-rank matrix completion (LRMC) has demonstrated remarkable success in a wide range of applications. To address the NP-hard nature of the rank minimization problem, the nuclear norm is commonly used as a convex and computationally tractable surrogate for the rank function. However, this approach often yields suboptimal solutions due to the excessive shrinkage of singular values. In this letter, we propose a novel reweighted logarithmic norm as a more effective nonconvex surrogate, which provides a closer approximation than many existing alternatives. We efficiently solve the resulting optimization problem by employing the alternating direction method of multipliers (ADMM). Experimental results on image inpainting demonstrate that the proposed method achieves superior performance compared to state-of-the-art LRMC approaches, both in terms of visual quality and quantitative metrics.

Support Driven Wavelet Frame-based Image Deblurring

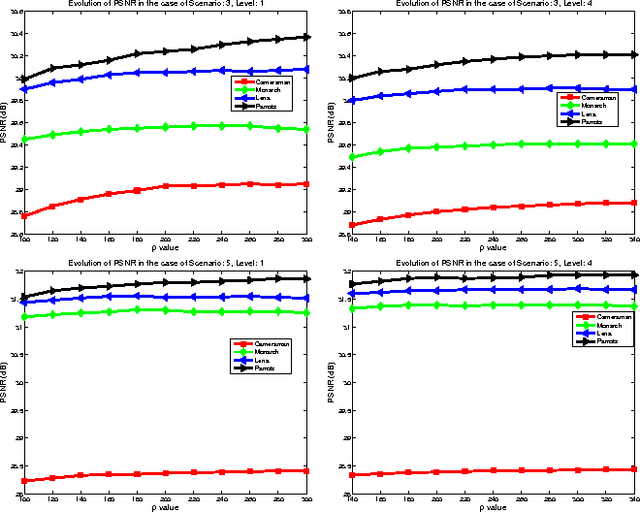
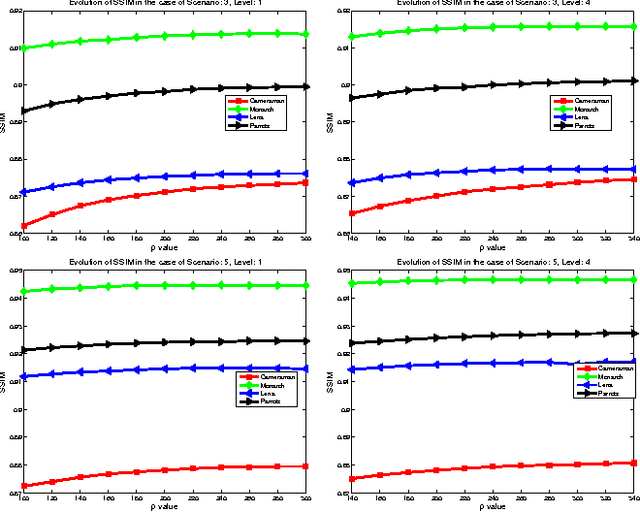
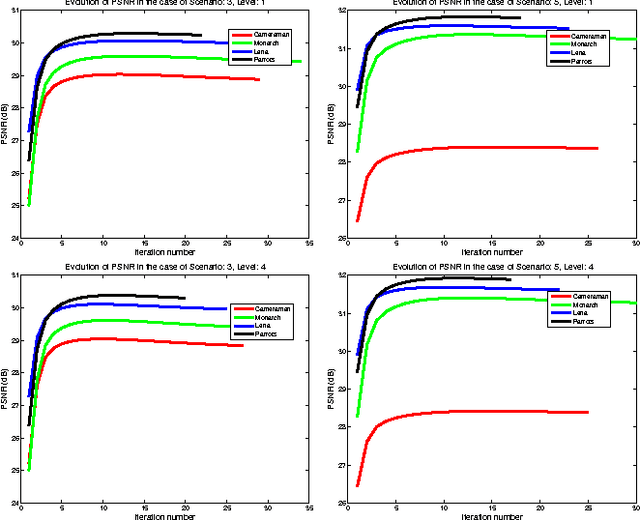
The wavelet frame systems have been playing an active role in image restoration and many other image processing fields over the past decades, owing to the good capability of sparsely approximating piece-wise smooth functions such as images. In this paper, we propose a novel wavelet frame based sparse recovery model called \textit{Support Driven Sparse Regularization} (SDSR) for image deblurring, where the partial support information of frame coefficients is attained via a self-learning strategy and exploited via the proposed truncated $\ell_0$ regularization. Moreover, the state-of-the-art image restoration methods can be naturally incorporated into our proposed wavelet frame based sparse recovery framework. In particular, in order to achieve reliable support estimation of the frame coefficients, we make use of the state-of-the-art image restoration result such as that from the IDD-BM3D method as the initial reference image for support estimation. Our extensive experimental results have shown convincing improvements over existing state-of-the-art deblurring methods.

Wavelet Frame Based Image Restoration Using Sparsity, Nonlocal and Support Prior of Frame Coefficients

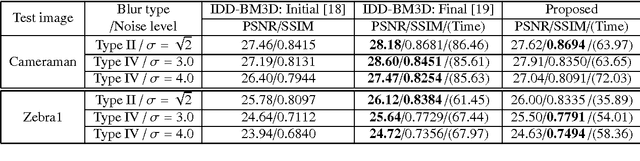
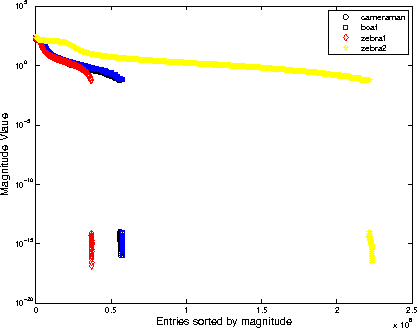
The wavelet frame systems have been widely investigated and applied for image restoration and many other image processing problems over the past decades, attributing to their good capability of sparsely approximating piece-wise smooth functions such as images. Most wavelet frame based models exploit the $l_1$ norm of frame coefficients for a sparsity constraint in the past. The authors in \cite{ZhangY2013, Dong2013} proposed an $l_0$ minimization model, where the $l_0$ norm of wavelet frame coefficients is penalized instead, and have demonstrated that significant improvements can be achieved compared to the commonly used $l_1$ minimization model. Very recently, the authors in \cite{Chen2015} proposed $l_0$-$l_2$ minimization model, where the nonlocal prior of frame coefficients is incorporated. This model proved to outperform the single $l_0$ minimization based model in terms of better recovered image quality. In this paper, we propose a truncated $l_0$-$l_2$ minimization model which combines sparsity, nonlocal and support prior of the frame coefficients. The extensive experiments have shown that the recovery results from the proposed regularization method performs better than existing state-of-the-art wavelet frame based methods, in terms of edge enhancement and texture preserving performance.

Linear Spatial Pyramid Matching Using Non-convex and non-negative Sparse Coding for Image Classification

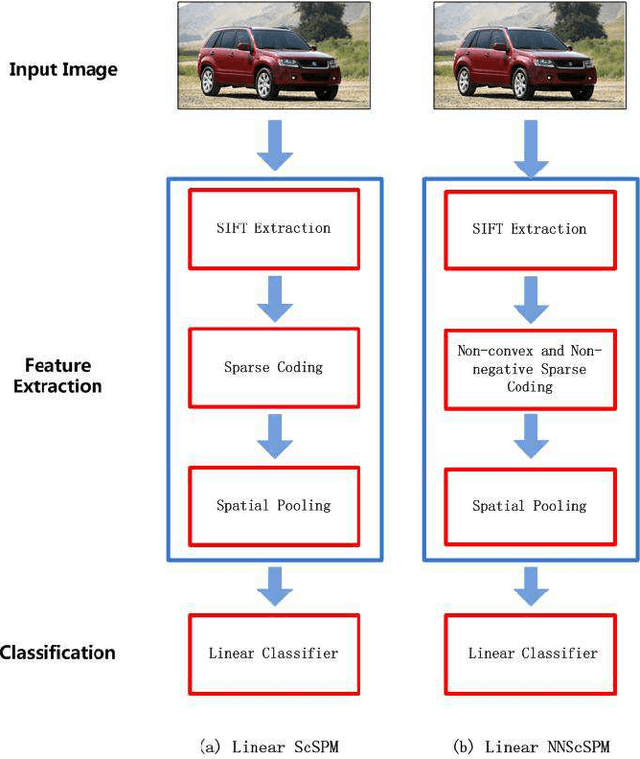
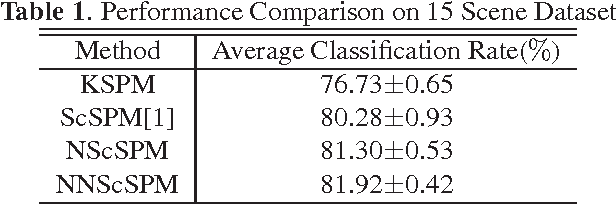
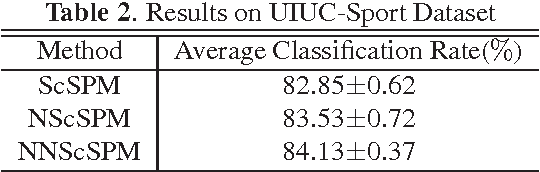
Recently sparse coding have been highly successful in image classification mainly due to its capability of incorporating the sparsity of image representation. In this paper, we propose an improved sparse coding model based on linear spatial pyramid matching(SPM) and Scale Invariant Feature Transform (SIFT ) descriptors. The novelty is the simultaneous non-convex and non-negative characters added to the sparse coding model. Our numerical experiments show that the improved approach using non-convex and non-negative sparse coding is superior than the original ScSPM[1] on several typical databases.