Leigh Sheneman
Markov Brains: A Technical Introduction
Sep 17, 2017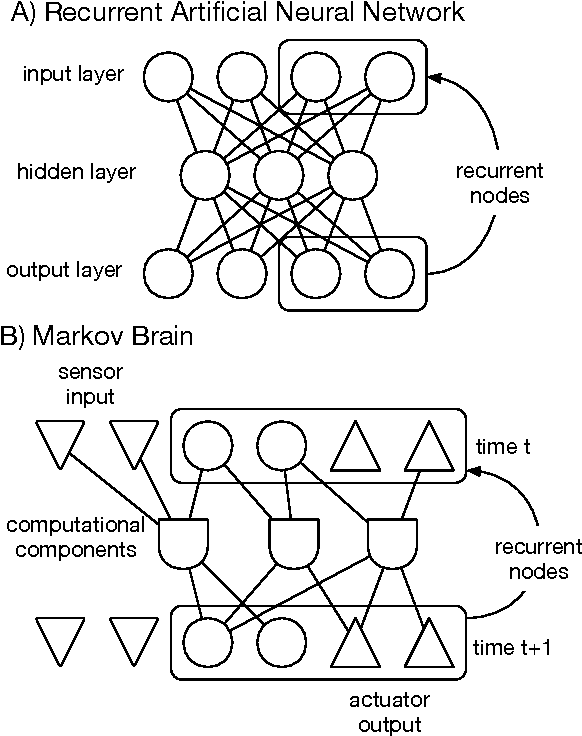
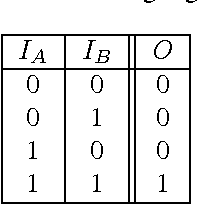
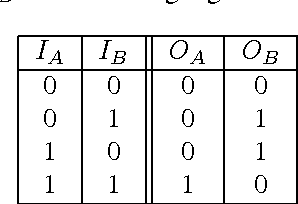

Abstract:Markov Brains are a class of evolvable artificial neural networks (ANN). They differ from conventional ANNs in many aspects, but the key difference is that instead of a layered architecture, with each node performing the same function, Markov Brains are networks built from individual computational components. These computational components interact with each other, receive inputs from sensors, and control motor outputs. The function of the computational components, their connections to each other, as well as connections to sensors and motors are all subject to evolutionary optimization. Here we describe in detail how a Markov Brain works, what techniques can be used to study them, and how they can be evolved.
Machine Learned Learning Machines
Aug 31, 2017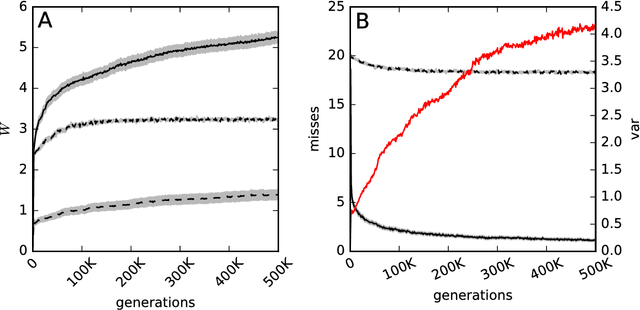


Abstract:There are two common approaches for optimizing the performance of a machine: genetic algorithms and machine learning. A genetic algorithm is applied over many generations whereas machine learning works by applying feedback until the system meets a performance threshold. Though these are methods that typically operate separately, we combine evolutionary adaptation and machine learning into one approach. Our focus is on machines that can learn during their lifetime, but instead of equipping them with a machine learning algorithm we aim to let them evolve their ability to learn by themselves. We use evolvable networks of probabilistic and deterministic logic gates, known as Markov Brains, as our computational model organism. The ability of Markov Brains to learn is augmented by a novel adaptive component that can change its computational behavior based on feedback. We show that Markov Brains can indeed evolve to incorporate these feedback gates to improve their adaptability to variable environments. By combining these two methods, we now also implemented a computational model that can be used to study the evolution of learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge