Testing Stationarity Concepts for ReLU Networks: Hardness, Regularity, and Robust Algorithms

We study the computational problem of the stationarity test for the empirical loss of neural networks with ReLU activation functions. Our contributions are: Hardness: We show that checking a certain first-order approximate stationarity concept for a piecewise linear function is co-NP-hard. This implies that testing a certain stationarity concept for a modern nonsmooth neural network is in general computationally intractable. As a corollary, we prove that testing so-called first-order minimality for functions in abs-normal form is co-NP-complete, which was conjectured by Griewank and Walther (2019, SIAM J. Optim., vol. 29, p284). Regularity: We establish a necessary and sufficient condition for the validity of an equality-type subdifferential chain rule in terms of Clarke, Fr\'echet, and limiting subdifferentials of the empirical loss of two-layer ReLU networks. This new condition is simple and efficiently checkable. Robust algorithms: We introduce an algorithmic scheme to test near-approximate stationarity in terms of both Clarke and Fr\'echet subdifferentials. Our scheme makes no false positive or false negative error when the tested point is sufficiently close to a stationary one and a certain qualification is satisfied. This is the first practical and robust stationarity test approach for two-layer ReLU networks.

Practical Schemes for Finding Near-Stationary Points of Convex Finite-Sums

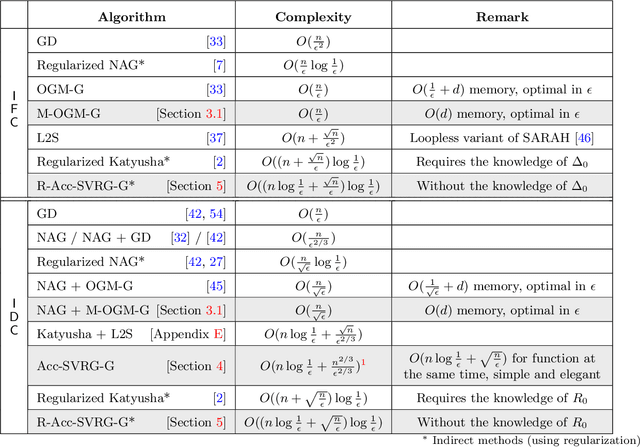
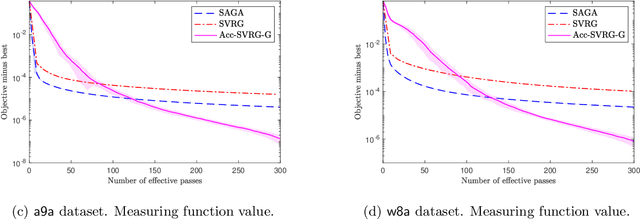
The problem of finding near-stationary points in convex optimization has not been adequately studied yet, unlike other optimality measures such as minimizing function value. Even in the deterministic case, the optimal method (OGM-G, due to Kim and Fessler (2021)) has just been discovered recently. In this work, we conduct a systematic study of the algorithmic techniques in finding near-stationary points of convex finite-sums. Our main contributions are several algorithmic discoveries: (1) we discover a memory-saving variant of OGM-G based on the performance estimation problem approach (Drori and Teboulle, 2014); (2) we design a new accelerated SVRG variant that can simultaneously achieve fast rates for both minimizing gradient norm and function value; (3) we propose an adaptively regularized accelerated SVRG variant, which does not require the knowledge of some unknown initial constants and achieves near-optimal complexities. We put an emphasis on the simplicity and practicality of the new schemes, which could facilitate future developments.

Learning Feature Sparse Principal Components

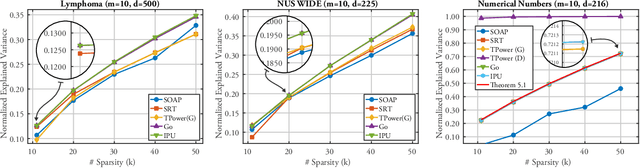
This paper presents new algorithms to solve the feature-sparsity constrained PCA problem (FSPCA), which performs feature selection and PCA simultaneously. Existing optimization methods for FSPCA require data distribution assumptions and are lack of global convergence guarantee. Though the general FSPCA problem is NP-hard, we show that, for a low-rank covariance, FSPCA can be solved globally (Algorithm 1). Then, we propose another strategy (Algorithm 2) to solve FSPCA for the general covariance by iteratively building a carefully designed proxy. We prove theoretical guarantees on approximation and convergence for the new algorithms. Experimental results show the promising performance of the new algorithms compared with the state-of-the-arts on both synthetic and real-world datasets.

A Comprehensive Survey for Low Rank Regularization

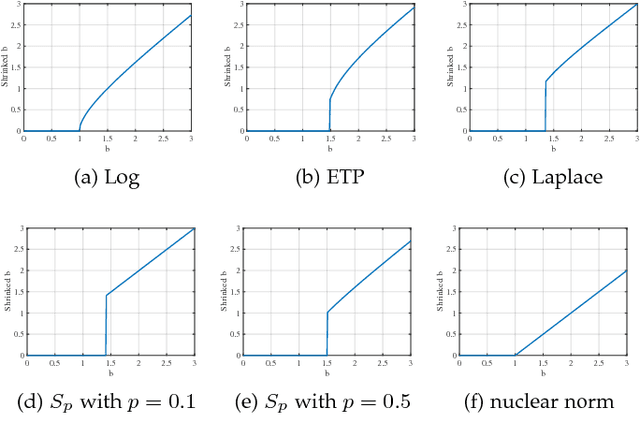
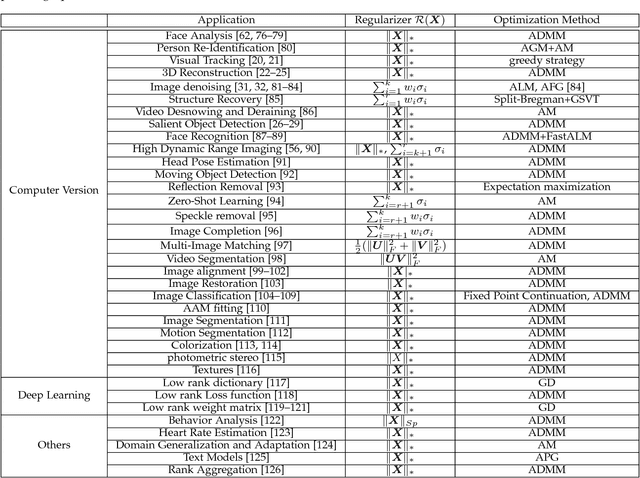
Low rank regularization, in essence, involves introducing a low rank or approximately low rank assumption for matrix we aim to learn, which has achieved great success in many fields including machine learning, data mining and computer version. Over the last decade, much progress has been made in theories and practical applications. Nevertheless, the intersection between them is very slight. In order to construct a bridge between practical applications and theoretical research, in this paper we provide a comprehensive survey for low rank regularization. We first review several traditional machine learning models using low rank regularization, and then show their (or their variants) applications in solving practical issues, such as non-rigid structure from motion and image denoising. Subsequently, we summarize the regularizers and optimization methods that achieve great success in traditional machine learning tasks but are rarely seen in solving practical issues. Finally, we provide a discussion and comparison for some representative regularizers including convex and non-convex relaxations. Extensive experimental results demonstrate that non-convex regularizers can provide a large advantage over the nuclear norm, the regularizer widely used in solving practical issues.