Solving excited states for long-range interacting trapped ions with neural networks

The computation of excited states in strongly interacting quantum many-body systems is of fundamental importance. Yet, it is notoriously challenging due to the exponential scaling of the Hilbert space dimension with the system size. Here, we introduce a neural network-based algorithm that can simultaneously output multiple low-lying excited states of a quantum many-body spin system in an accurate and efficient fashion. This algorithm, dubbed the neural quantum excited-state (NQES) algorithm, requires no explicit orthogonalization of the states and is generally applicable to higher dimensions. We demonstrate, through concrete examples including the Haldane-Shastry model with all-to-all interactions, that the NQES algorithm is capable of efficiently computing multiple excited states and their related observable expectations. In addition, we apply the NQES algorithm to two classes of long-range interacting trapped-ion systems in a two-dimensional Wigner crystal. For non-decaying all-to-all interactions with alternating signs, our computed low-lying excited states bear spatial correlation patterns similar to those of the ground states, which closely match recent experimental observations that the quasi-adiabatically prepared state accurately reproduces analytical ground-state correlations. For a system of up to 300 ions with power-law decaying antiferromagnetic interactions, we successfully uncover its gap scaling and correlation features. Our results establish a scalable and efficient algorithm for computing excited states of interacting quantum many-body systems, which holds potential applications ranging from benchmarking quantum devices to photoisomerization.

Quantum automated learning with provable and explainable trainability

Machine learning is widely believed to be one of the most promising practical applications of quantum computing. Existing quantum machine learning schemes typically employ a quantum-classical hybrid approach that relies crucially on gradients of model parameters. Such an approach lacks provable convergence to global minima and will become infeasible as quantum learning models scale up. Here, we introduce quantum automated learning, where no variational parameter is involved and the training process is converted to quantum state preparation. In particular, we encode training data into unitary operations and iteratively evolve a random initial state under these unitaries and their inverses, with a target-oriented perturbation towards higher prediction accuracy sandwiched in between. Under reasonable assumptions, we rigorously prove that the evolution converges exponentially to the desired state corresponding to the global minimum of the loss function. We show that such a training process can be understood from the perspective of preparing quantum states by imaginary time evolution, where the data-encoded unitaries together with target-oriented perturbations would train the quantum learning model in an automated fashion. We further prove that the quantum automated learning paradigm features good generalization ability with the generalization error upper bounded by the ratio between a logarithmic function of the Hilbert space dimension and the number of training samples. In addition, we carry out extensive numerical simulations on real-life images and quantum data to demonstrate the effectiveness of our approach and validate the assumptions. Our results establish an unconventional quantum learning strategy that is gradient-free with provable and explainable trainability, which would be crucial for large-scale practical applications of quantum computing in machine learning scenarios.

Quantum Capsule Networks

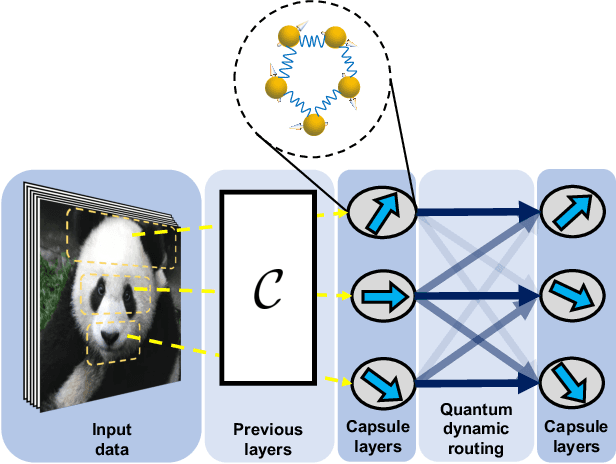
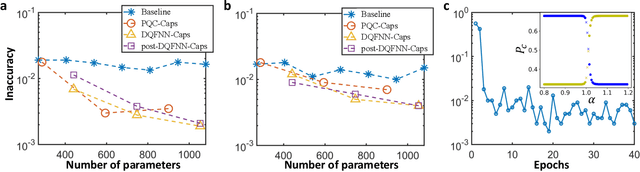
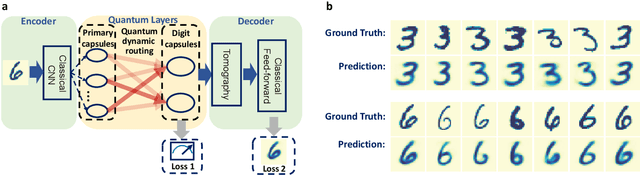
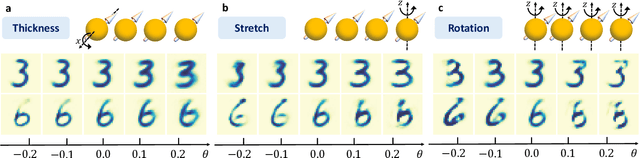
Capsule networks, which incorporate the paradigms of connectionism and symbolism, have brought fresh insights into artificial intelligence. The capsule, as the building block of capsule networks, is a group of neurons represented by a vector to encode different features of an entity. The information is extracted hierarchically through capsule layers via routing algorithms. Here, we introduce a quantum capsule network (dubbed QCapsNet) together with a quantum dynamic routing algorithm. Our model enjoys an exponential speedup in the dynamic routing process and exhibits an enhanced representation power. To benchmark the performance of the QCapsNet, we carry out extensive numerical simulations on the classification of handwritten digits and symmetry-protected topological phases, and show that the QCapsNet can achieve the state-of-the-art accuracy and outperforms conventional quantum classifiers evidently. We further unpack the output capsule state and find that a particular subspace may correspond to a human-understandable feature of the input data, which indicates the potential explainability of such networks. Our work reveals an intriguing prospect of quantum capsule networks in quantum machine learning, which may provide a valuable guide towards explainable quantum artificial intelligence.