PySensors 2.0: A Python Package for Sparse Sensor Placement

PySensors is a Python package for selecting and placing a sparse set of sensors for reconstruction and classification tasks. In this major update to \texttt{PySensors}, we introduce spatially constrained sensor placement capabilities, allowing users to enforce constraints such as maximum or exact sensor counts in specific regions, incorporate predetermined sensor locations, and maintain minimum distances between sensors. We extend functionality to support custom basis inputs, enabling integration of any data-driven or spectral basis. We also propose a thermodynamic approach that goes beyond a single ``optimal'' sensor configuration and maps the complete landscape of sensor interactions induced by the training data. This comprehensive view facilitates integration with external selection criteria and enables assessment of sensor replacement impacts. The new optimization technique also accounts for over- and under-sampling of sensors, utilizing a regularized least squares approach for robust reconstruction. Additionally, we incorporate noise-induced uncertainty quantification of the estimation error and provide visual uncertainty heat maps to guide deployment decisions. To highlight these additions, we provide a brief description of the mathematical algorithms and theory underlying these new capabilities. We demonstrate the usage of new features with illustrative code examples and include practical advice for implementation across various application domains. Finally, we outline a roadmap of potential extensions to further enhance the package's functionality and applicability to emerging sensing challenges.

Reservoir computing for system identification and predictive control with limited data

Model predictive control (MPC) is an industry standard control technique that iteratively solves an open-loop optimization problem to guide a system towards a desired state or trajectory. Consequently, an accurate forward model of system dynamics is critical for the efficacy of MPC and much recent work has been aimed at the use of neural networks to act as data-driven surrogate models to enable MPC. Perhaps the most common network architecture applied to this task is the recurrent neural network (RNN) due to its natural interpretation as a dynamical system. In this work, we assess the ability of RNN variants to both learn the dynamics of benchmark control systems and serve as surrogate models for MPC. We find that echo state networks (ESNs) have a variety of benefits over competing architectures, namely reductions in computational complexity, longer valid prediction times, and reductions in cost of the MPC objective function.

Data-Driven Ergonomic Risk Assessment of Complex Hand-intensive Manufacturing Processes

Hand-intensive manufacturing processes, such as composite layup and textile draping, require significant human dexterity to accommodate task complexity. These strenuous hand motions often lead to musculoskeletal disorders and rehabilitation surgeries. We develop a data-driven ergonomic risk assessment system with a special focus on hand and finger activity to better identify and address ergonomic issues related to hand-intensive manufacturing processes. The system comprises a multi-modal sensor testbed to collect and synchronize operator upper body pose, hand pose and applied forces; a Biometric Assessment of Complete Hand (BACH) formulation to measure high-fidelity hand and finger risks; and industry-standard risk scores associated with upper body posture, RULA, and hand activity, HAL. Our findings demonstrate that BACH captures injurious activity with a higher granularity in comparison to the existing metrics. Machine learning models are also used to automate RULA and HAL scoring, and generalize well to unseen participants. Our assessment system, therefore, provides ergonomic interpretability of the manufacturing processes studied, and could be used to mitigate risks through minor workplace optimization and posture corrections.

Statistical Mechanics of Dynamical System Identification

Recovering dynamical equations from observed noisy data is the central challenge of system identification. We develop a statistical mechanical approach to analyze sparse equation discovery algorithms, which typically balance data fit and parsimony through a trial-and-error selection of hyperparameters. In this framework, statistical mechanics offers tools to analyze the interplay between complexity and fitness, in analogy to that done between entropy and energy. To establish this analogy, we define the optimization procedure as a two-level Bayesian inference problem that separates variable selection from coefficient values and enables the computation of the posterior parameter distribution in closed form. A key advantage of employing statistical mechanical concepts, such as free energy and the partition function, is in the quantification of uncertainty, especially in in the low-data limit; frequently encountered in real-world applications. As the data volume increases, our approach mirrors the thermodynamic limit, leading to distinct sparsity- and noise-induced phase transitions that delineate correct from incorrect identification. This perspective of sparse equation discovery, is versatile and can be adapted to various other equation discovery algorithms.

Data-Induced Interactions of Sparse Sensors

Large-dimensional empirical data in science and engineering frequently has low-rank structure and can be represented as a combination of just a few eigenmodes. Because of this structure, we can use just a few spatially localized sensor measurements to reconstruct the full state of a complex system. The quality of this reconstruction, especially in the presence of sensor noise, depends significantly on the spatial configuration of the sensors. Multiple algorithms based on gappy interpolation and QR factorization have been proposed to optimize sensor placement. Here, instead of an algorithm that outputs a singular "optimal" sensor configuration, we take a thermodynamic view to compute the full landscape of sensor interactions induced by the training data. The landscape takes the form of the Ising model in statistical physics, and accounts for both the data variance captured at each sensor location and the crosstalk between sensors. Mapping out these data-induced sensor interactions allows combining them with external selection criteria and anticipating sensor replacement impacts.

Optimal Sensor Placement with Adaptive Constraints for Nuclear Digital Twins

Given harsh operating conditions and physical constraints in reactors, nuclear applications cannot afford to equip the physical asset with a large array of sensors. Therefore, it is crucial to carefully determine the placement of sensors within the given spatial limitations, enabling the reconstruction of reactor flow fields and the creation of nuclear digital twins. Various design considerations are imposed, such as predetermined sensor locations, restricted areas within the reactor, a fixed number of sensors allocated to a specific region, or sensors positioned at a designated distance from one another. We develop a data-driven technique that integrates constraints into an optimization procedure for sensor placement, aiming to minimize reconstruction errors. Our approach employs a greedy algorithm that can optimize sensor locations on a grid, adhering to user-defined constraints. We demonstrate the near optimality of our algorithm by computing all possible configurations for selecting a certain number of sensors for a randomly generated state space system. In this work, the algorithm is demonstrated on the Out-of-Pile Testing and Instrumentation Transient Water Irradiation System (OPTI-TWIST) prototype vessel, which is electrically heated to mimic the neutronics effect of the Transient Reactor Test facility (TREAT) at Idaho National Laboratory (INL). The resulting sensor-based reconstruction of temperature within the OPTI-TWIST minimizes error, provides probabilistic bounds for noise-induced uncertainty and will finally be used for communication between the digital twin and experimental facility.

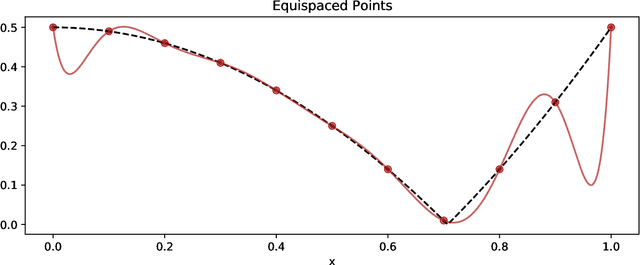
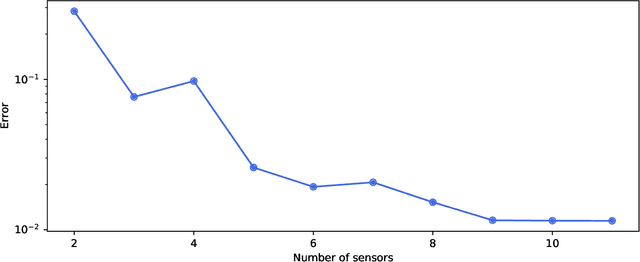
PySensors: A Python Package for Sparse Sensor Placement

PySensors is a Python package for selecting and placing a sparse set of sensors for classification and reconstruction tasks. Specifically, PySensors implements algorithms for data-driven sparse sensor placement optimization for reconstruction (SSPOR) and sparse sensor placement optimization for classification (SSPOC). In this work we provide a brief description of the mathematical algorithms and theory for sparse sensor optimization, along with an overview and demonstration of the features implemented in PySensors (with code examples). We also include practical advice for user and a list of potential extensions to PySensors. Software is available at https://github.com/dynamicslab/pysensors.

Data-Driven Aerospace Engineering: Reframing the Industry with Machine Learning

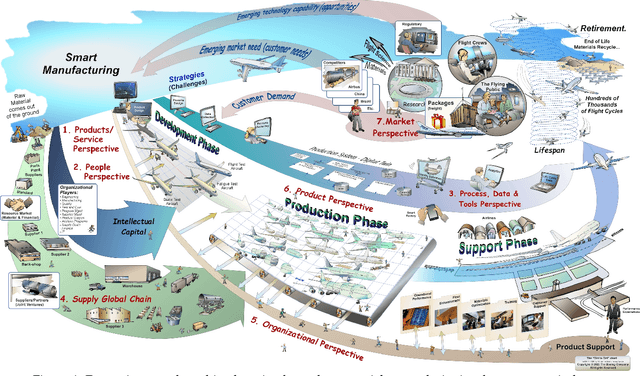
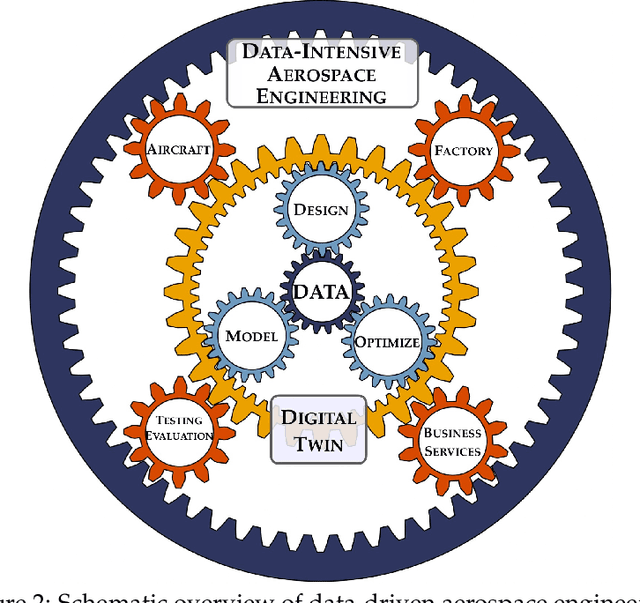
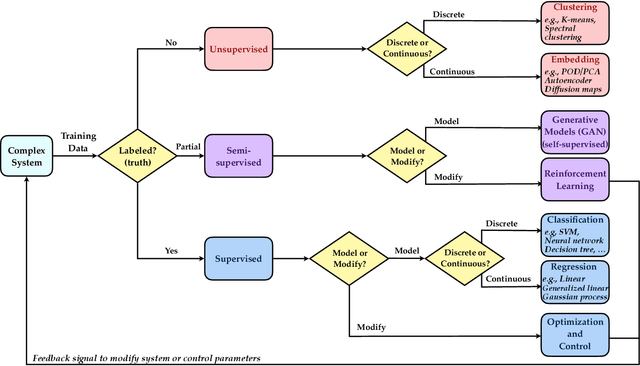
Data science, and machine learning in particular, is rapidly transforming the scientific and industrial landscapes. The aerospace industry is poised to capitalize on big data and machine learning, which excels at solving the types of multi-objective, constrained optimization problems that arise in aircraft design and manufacturing. Indeed, emerging methods in machine learning may be thought of as data-driven optimization techniques that are ideal for high-dimensional, non-convex, and constrained, multi-objective optimization problems, and that improve with increasing volumes of data. In this review, we will explore the opportunities and challenges of integrating data-driven science and engineering into the aerospace industry. Importantly, we will focus on the critical need for interpretable, generalizeable, explainable, and certifiable machine learning techniques for safety-critical applications. This review will include a retrospective, an assessment of the current state-of-the-art, and a roadmap looking forward. Recent algorithmic and technological trends will be explored in the context of critical challenges in aerospace design, manufacturing, verification, validation, and services. In addition, we will explore this landscape through several case studies in the aerospace industry. This document is the result of close collaboration between UW and Boeing to summarize past efforts and outline future opportunities.

Kernel Analog Forecasting: Multiscale Test Problems

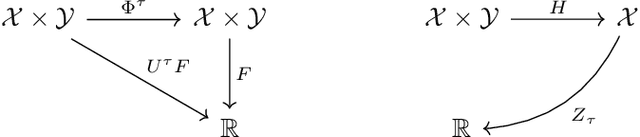
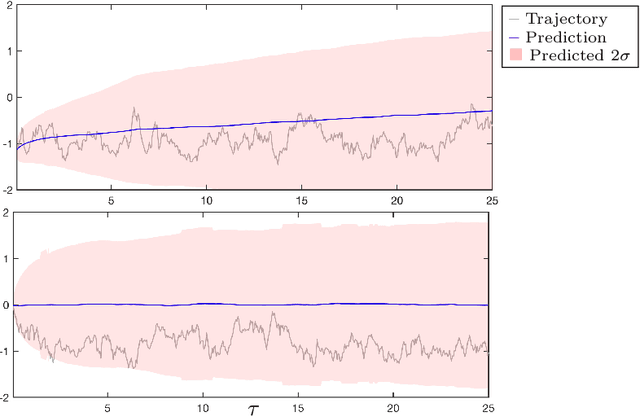
Data-driven prediction is becoming increasingly widespread as the volume of data available grows and as algorithmic development matches this growth. The nature of the predictions made, and the manner in which they should be interpreted, depends crucially on the extent to which the variables chosen for prediction are Markovian, or approximately Markovian. Multiscale systems provide a framework in which this issue can be analyzed. In this work kernel analog forecasting methods are studied from the perspective of data generated by multiscale dynamical systems. The problems chosen exhibit a variety of different Markovian closures, using both averaging and homogenization; furthermore, settings where scale-separation is not present and the predicted variables are non-Markovian, are also considered. The studies provide guidance for the interpretation of data-driven prediction methods when used in practice.

Sparse Principal Component Analysis via Variable Projection

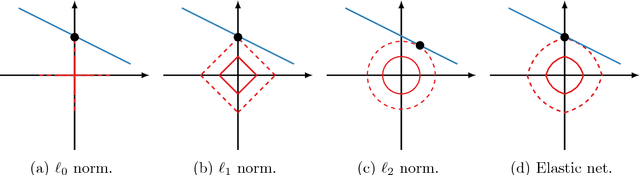
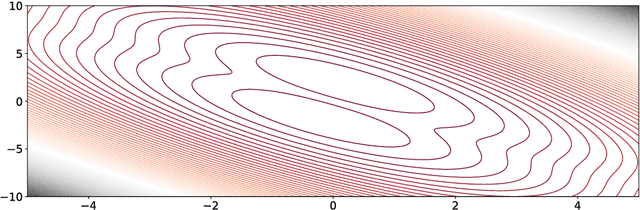
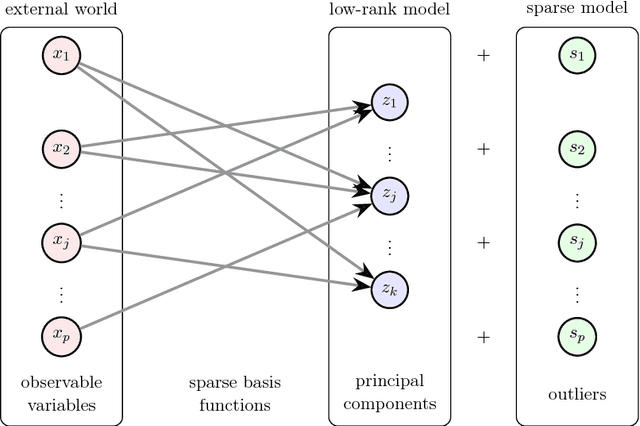
Sparse principal component analysis (SPCA) has emerged as a powerful technique for data analysis, providing improved interpretation of low-rank structures by identifying localized spatial structures in the data and disambiguating between distinct time scales. We demonstrate a robust and scalable SPCA algorithm by formulating it as a value-function optimization problem. This viewpoint leads to a flexible and computationally efficient algorithm. It can further leverage randomized methods from linear algebra to extend the approach to the large-scale (big data) setting. Our proposed innovation also allows for a robust SPCA formulation which can obtain meaningful sparse components in spite of grossly corrupted input data. The proposed algorithms are demonstrated using both synthetic and real world data, showing exceptional computational efficiency and diagnostic performance.