Edge Sampling of Graphs: Graph Signal Processing Approach With Edge Smoothness

Finding important edges in a graph is a crucial problem for various research fields, such as network epidemics, signal processing, machine learning, and sensor networks. In this paper, we tackle the problem based on sampling theory on graphs. We convert the original graph to a line graph where its nodes and edges, respectively, represent the original edges and the connections between the edges. We then perform node sampling of the line graph based on the edge smoothness assumption: This process selects the most critical edges in the original graph. We present a general framework of edge sampling based on graph sampling theory and reveal a theoretical relationship between the degree of the original graph and the line graph. We also propose an acceleration method for edge sampling in the proposed framework by using the relationship between two types of Laplacian of the node and edge domains. Experimental results in synthetic and real-world graphs validate the effectiveness of our approach against some alternative edge selection methods.

Versatile Time-Frequency Representations Realized by Convex Penalty on Magnitude Spectrogram

Sparse time-frequency (T-F) representations have been an important research topic for more than several decades. Among them, optimization-based methods (in particular, extensions of basis pursuit) allow us to design the representations through objective functions. Since acoustic signal processing utilizes models of spectrogram, the flexibility of optimization-based T-F representations is helpful for adjusting the representation for each application. However, acoustic applications often require models of \textit{magnitude} of T-F representations obtained by discrete Gabor transform (DGT). Adjusting a T-F representation to such a magnitude model (e.g., smoothness of magnitude of DGT coefficients) results in a non-convex optimization problem that is difficult to solve. In this paper, instead of tackling difficult non-convex problems, we propose a convex optimization-based framework that realizes a T-F representation whose magnitude has characteristics specified by the user. We analyzed the properties of the proposed method and provide numerical examples of sparse T-F representations having, e.g., low-rank or smooth magnitude, which have not been realized before.

Clustering of Time-Varying Graphs Based on Temporal Label Smoothness

We propose a node clustering method for time-varying graphs based on the assumption that the cluster labels are changed smoothly over time. Clustering is one of the fundamental tasks in many science and engineering fields including signal processing, machine learning, and data mining. Although most existing studies focus on the clustering of nodes in static graphs, we often encounter time-varying graphs for time-series data, e.g., social networks, brain functional connectivity, and point clouds. In this paper, we formulate a node clustering of time-varying graphs as an optimization problem based on spectral clustering, with a smoothness constraint of the node labels. We solve the problem with a primal-dual splitting algorithm. Experiments on synthetic and real-world time-varying graphs are performed to validate the effectiveness of the proposed approach.

Graph Filter Transfer via Probability Density Ratio Weighting

The problem of recovering graph signals is one of the main topics in graph signal processing. A representative approach to this problem is the graph Wiener filter, which utilizes the statistical information of the target signal computed from historical data to construct an effective estimator. However, we often encounter situations where the current graph differs from that of historical data due to topology changes, leading to performance degradation of the estimator. This paper proposes a graph filter transfer method, which learns an effective estimator from historical data under topology changes. The proposed method leverages the probability density ratio of the current and historical observations and constructs an estimator that minimizes the reconstruction error in the current graph domain. The experiment on synthetic data demonstrates that the proposed method outperforms other methods.

Graph Signal Restoration Using Nested Deep Algorithm Unrolling

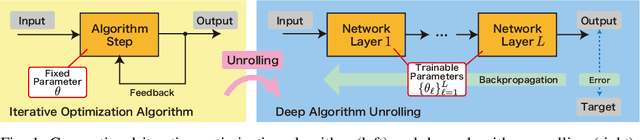
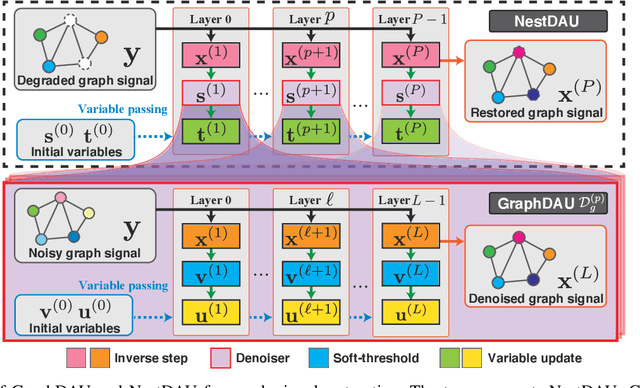
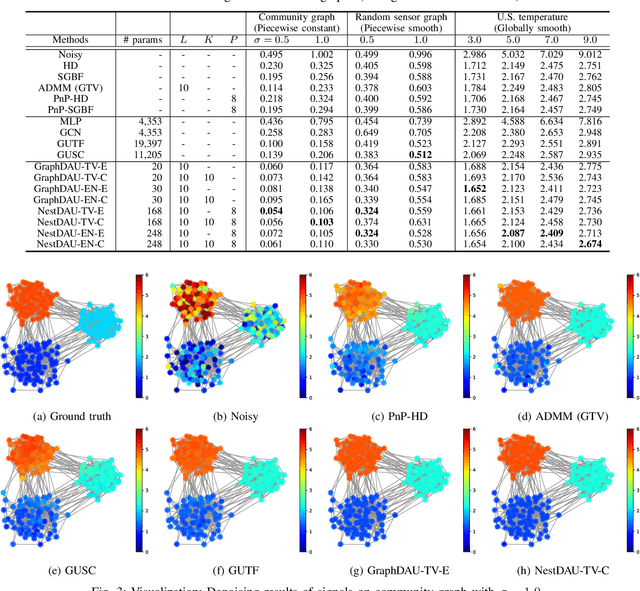
Graph signal processing is a ubiquitous task in many applications such as sensor, social, transportation and brain networks, point cloud processing, and graph neural networks. Graph signals are often corrupted through sensing processes, and need to be restored for the above applications. In this paper, we propose two graph signal restoration methods based on deep algorithm unrolling (DAU). First, we present a graph signal denoiser by unrolling iterations of the alternating direction method of multiplier (ADMM). We then propose a general restoration method for linear degradation by unrolling iterations of Plug-and-Play ADMM (PnP-ADMM). In the second method, the unrolled ADMM-based denoiser is incorporated as a submodule. Therefore, our restoration method has a nested DAU structure. Thanks to DAU, parameters in the proposed denoising/restoration methods are trainable in an end-to-end manner. Since the proposed restoration methods are based on iterations of a (convex) optimization algorithm, the method is interpretable and keeps the number of parameters small because we only need to tune graph-independent regularization parameters. We solve two main problems in existing graph signal restoration methods: 1) limited performance of convex optimization algorithms due to fixed parameters which are often determined manually. 2) large number of parameters of graph neural networks that result in difficulty of training. Several experiments for graph signal denoising and interpolation are performed on synthetic and real-world data. The proposed methods show performance improvements to several existing methods in terms of root mean squared error in both tasks.

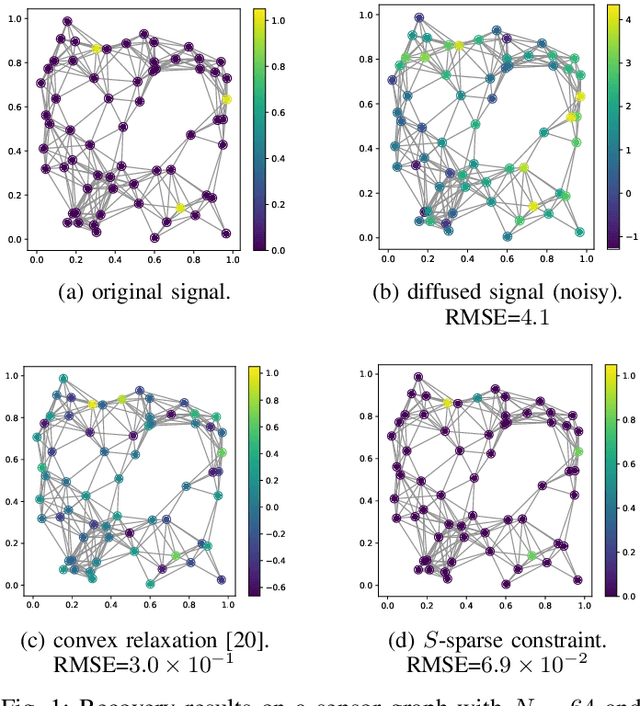
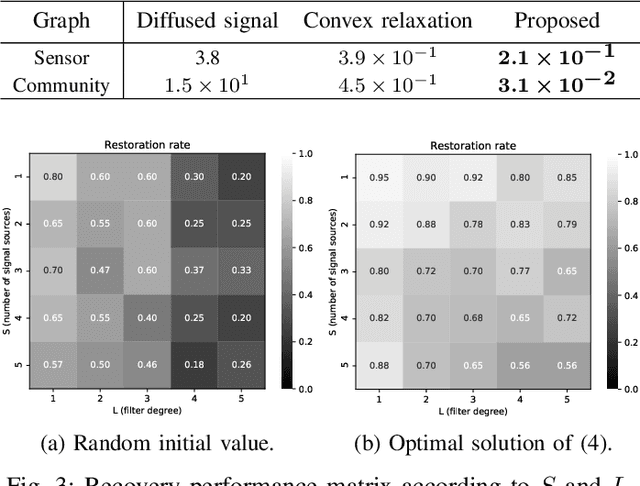
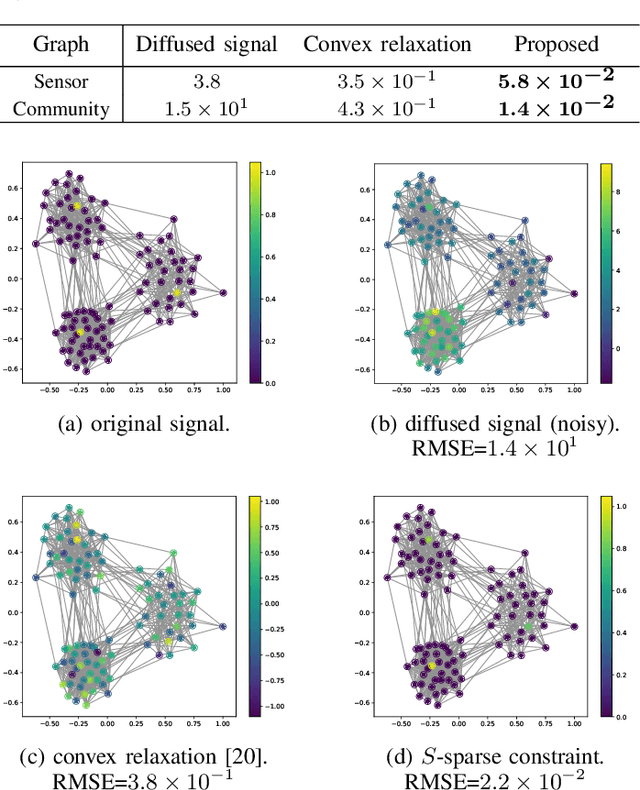
Graph Blind Deconvolution with Sparseness Constraint

We propose a blind deconvolution method for signals on graphs, with the exact sparseness constraint for the original signal. Graph blind deconvolution is an algorithm for estimating the original signal on a graph from a set of blurred and noisy measurements. Imposing a constraint on the number of nonzero elements is desirable for many different applications. This paper deals with the problem with constraints placed on the exact number of original sources, which is given by an optimization problem with an $\ell_0$ norm constraint. We solve this non-convex optimization problem using the ADMM iterative solver. Numerical experiments using synthetic signals demonstrate the effectiveness of the proposed method.

Time-Varying Graph Learning with Constraints on Graph Temporal Variation

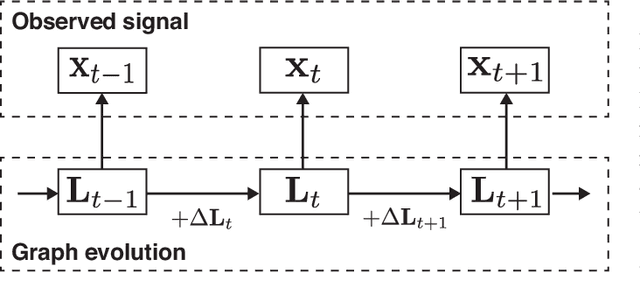
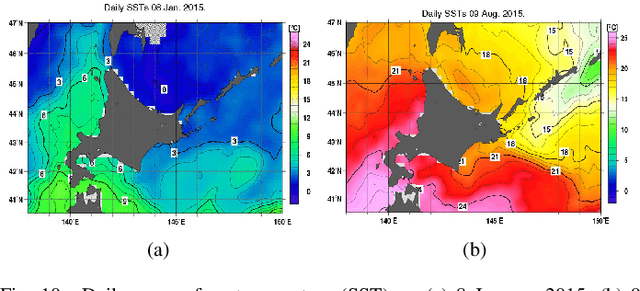
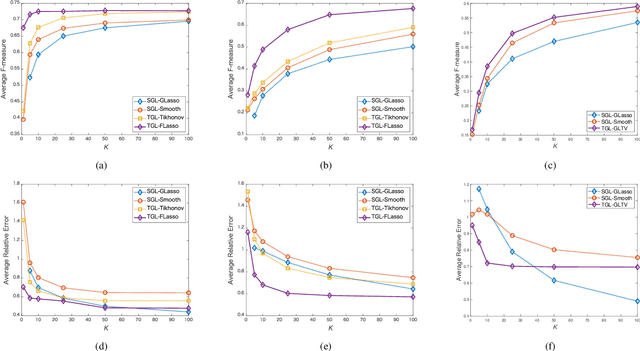
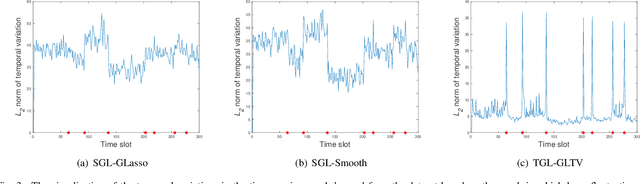
We propose a novel framework for learning time-varying graphs from spatiotemporal measurements. Given an appropriate prior on the temporal behavior of signals, our proposed method can estimate time-varying graphs from a small number of available measurements. To achieve this, we introduce two regularization terms in convex optimization problems that constrain sparseness of temporal variations of the time-varying networks. Moreover, a computationally-scalable algorithm is introduced to efficiently solve the optimization problem. The experimental results with synthetic and real datasets (point cloud and temperature data) demonstrate our proposed method outperforms the existing state-of-the-art methods.