Zohir Bouzid
LIP6
Wait-Free Gathering of Mobile Robots
Jul 01, 2012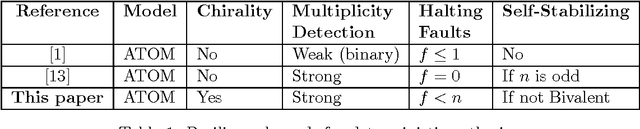

Abstract:The problem of gathering multiple mobile robots to a single location, is one of the fundamental problems in distributed coordination between autonomous robots. The problem has been studied and solved even for robots that are anonymous, disoriented, memoryless and operate in the semi-synchronous (ATOM) model. However all known solutions require the robots to be faulty-free except for the results of [Agmon and Peleg 2006] who solve the gathering problem in presence of one crash fault. This leaves open the question of whether gathering of correct robots can be achieved in the presence of multiple crash failures. We resolve the question in this paper and show how to solve gathering, when any number of robots may crash at any time during the algorithm, assuming strong multiplicity detection and chirality. In contrast it is known that for the more stronger byzantine faults, it is impossible to gather even in a 3-robot system if one robot is faulty. Our algorithm solves the gathering of correct robots in the semi-synchronous model where an adversary may stop any robot before reaching its desired destination. Further the algorithm is self-stabilizing as it achieves gathering starting from any configuration (except the bivalent configuration where deterministic gathering is impossible).
The BG-simulation for Byzantine Mobile Robots
Jun 01, 2011Abstract:This paper investigates the task solvability of mobile robot systems subject to Byzantine faults. We first consider the gathering problem, which requires all robots to meet in finite time at a non-predefined location. It is known that the solvability of Byzantine gathering strongly depends on a number of system attributes, such as synchrony, the number of Byzantine robots, scheduling strategy, obliviousness, orientation of local coordinate systems and so on. However, the complete characterization of the attributes making Byzantine gathering solvable still remains open. In this paper, we show strong impossibility results of Byzantine gathering. Namely, we prove that Byzantine gathering is impossible even if we assume one Byzantine fault, an atomic execution system, the n-bounded centralized scheduler, non-oblivious robots, instantaneous movements and a common orientation of local coordinate systems (where n denote the number of correct robots). Those hypotheses are much weaker than used in previous work, inducing a much stronger impossibility result. At the core of our impossibility result is a reduction from the distributed consensus problem in asynchronous shared-memory systems. In more details, we newly construct a generic reduction scheme based on the distributed BG-simulation. Interestingly, because of its versatility, we can easily extend our impossibility result for general pattern formation problems.
RoboCast: Asynchronous Communication in Robot Networks
Sep 23, 2010
Abstract:This paper introduces the \emph{RoboCast} communication abstraction. The RoboCast allows a swarm of non oblivious, anonymous robots that are only endowed with visibility sensors and do not share a common coordinate system, to asynchronously exchange information. We propose a generic framework that covers a large class of asynchronous communication algorithms and show how our framework can be used to implement fundamental building blocks in robot networks such as gathering or stigmergy. In more details, we propose a RoboCast algorithm that allows robots to broadcast their local coordinate systems to each others. Our algorithm is further refined with a local collision avoidance scheme. Then, using the RoboCast primitive, we propose algorithms for deterministic asynchronous gathering and binary information exchange.
Byzantine Convergence in Robots Networks: The Price of Asynchrony
Aug 04, 2009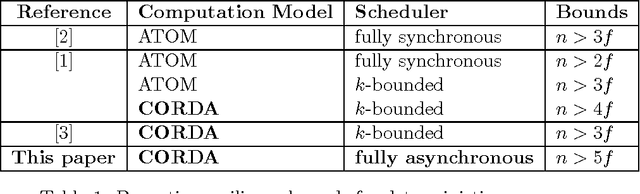
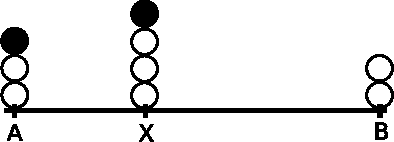
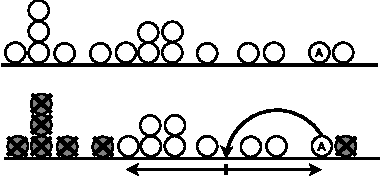
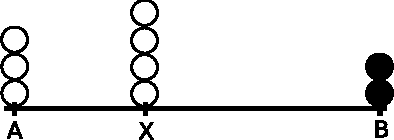
Abstract:We study the convergence problem in fully asynchronous, uni-dimensional robot networks that are prone to Byzantine (i.e. malicious) failures. In these settings, oblivious anonymous robots with arbitrary initial positions are required to eventually converge to an a apriori unknown position despite a subset of them exhibiting Byzantine behavior. Our contribution is twofold. We propose a deterministic algorithm that solves the problem in the most generic settings: fully asynchronous robots that operate in the non-atomic CORDA model. Our algorithm provides convergence in 5f+1-sized networks where f is the upper bound on the number of Byzantine robots. Additionally, we prove that 5f+1 is a lower bound whenever robot scheduling is fully asynchronous. This constrasts with previous results in partially synchronous robots networks, where 3f+1 robots are necessary and sufficient.
Optimal Byzantine Resilient Convergence in Asynchronous Robot Networks
Jun 03, 2009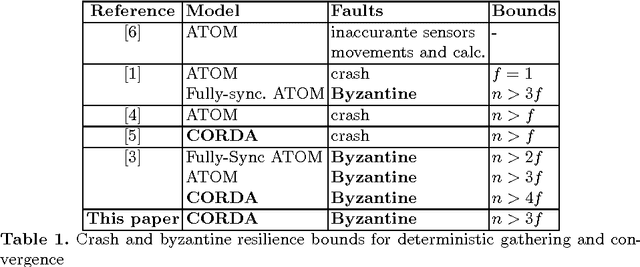
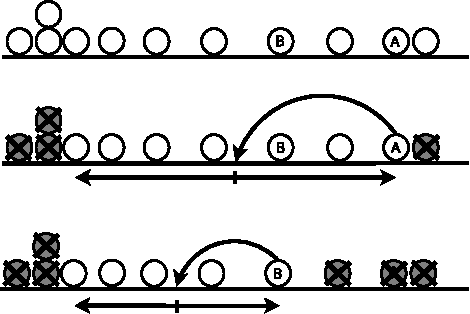
Abstract:We propose the first deterministic algorithm that tolerates up to $f$ byzantine faults in $3f+1$-sized networks and performs in the asynchronous CORDA model. Our solution matches the previously established lower bound for the semi-synchronous ATOM model on the number of tolerated Byzantine robots. Our algorithm works under bounded scheduling assumptions for oblivious robots moving in a uni-dimensional space.
Optimal byzantine resilient convergence in oblivious robot networks
May 25, 2009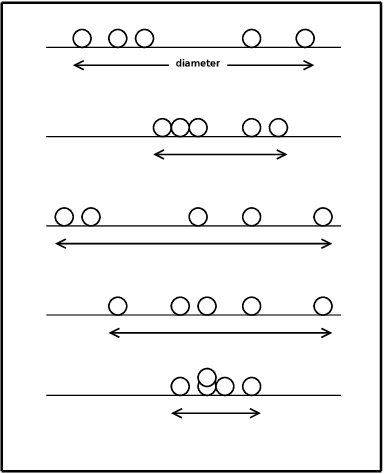
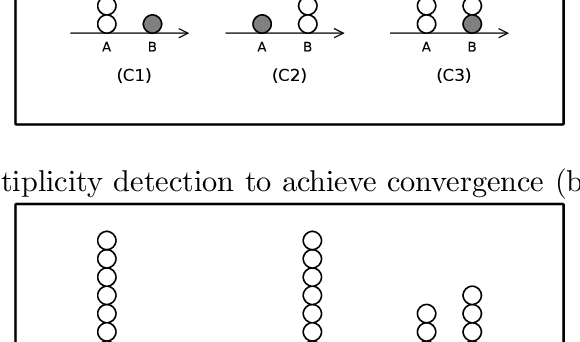
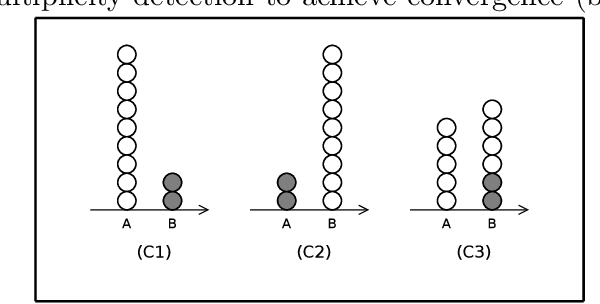
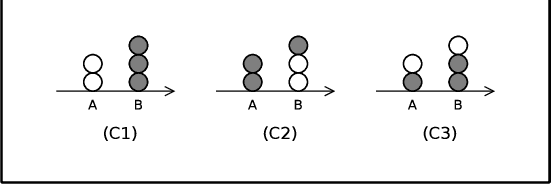
Abstract:Given a set of robots with arbitrary initial location and no agreement on a global coordinate system, convergence requires that all robots asymptotically approach the exact same, but unknown beforehand, location. Robots are oblivious-- they do not recall the past computations -- and are allowed to move in a one-dimensional space. Additionally, robots cannot communicate directly, instead they obtain system related information only via visual sensors. We draw a connection between the convergence problem in robot networks, and the distributed \emph{approximate agreement} problem (that requires correct processes to decide, for some constant $\epsilon$, values distance $\epsilon$ apart and within the range of initial proposed values). Surprisingly, even though specifications are similar, the convergence implementation in robot networks requires specific assumptions about synchrony and Byzantine resilience. In more details, we prove necessary and sufficient conditions for the convergence of mobile robots despite a subset of them being Byzantine (i.e. they can exhibit arbitrary behavior). Additionally, we propose a deterministic convergence algorithm for robot networks and analyze its correctness and complexity in various synchrony settings. The proposed algorithm tolerates f Byzantine robots for (2f+1)-sized robot networks in fully synchronous networks, (3f+1)-sized in semi-synchronous networks. These bounds are optimal for the class of cautious algorithms, which guarantee that correct robots always move inside the range of positions of the correct robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge