Is Certifying $\ell_p$ Robustness Still Worthwhile?

Over the years, researchers have developed myriad attacks that exploit the ubiquity of adversarial examples, as well as defenses that aim to guard against the security vulnerabilities posed by such attacks. Of particular interest to this paper are defenses that provide provable guarantees against the class of $\ell_p$-bounded attacks. Certified defenses have made significant progress, taking robustness certification from toy models and datasets to large-scale problems like ImageNet classification. While this is undoubtedly an interesting academic problem, as the field has matured, its impact in practice remains unclear, thus we find it useful to revisit the motivation for continuing this line of research. There are three layers to this inquiry, which we address in this paper: (1) why do we care about robustness research? (2) why do we care about the $\ell_p$-bounded threat model? And (3) why do we care about certification as opposed to empirical defenses? In brief, we take the position that local robustness certification indeed confers practical value to the field of machine learning. We focus especially on the latter two questions from above. With respect to the first of the two, we argue that the $\ell_p$-bounded threat model acts as a minimal requirement for safe application of models in security-critical domains, while at the same time, evidence has mounted suggesting that local robustness may lead to downstream external benefits not immediately related to robustness. As for the second, we argue that (i) certification provides a resolution to the cat-and-mouse game of adversarial attacks; and furthermore, that (ii) perhaps contrary to popular belief, there may not exist a fundamental trade-off between accuracy, robustness, and certifiability, while moreover, certified training techniques constitute a particularly promising way for learning robust models.

A Recipe for Improved Certifiable Robustness: Capacity and Data

A key challenge, supported both theoretically and empirically, is that robustness demands greater network capacity and more data than standard training. However, effectively adding capacity under stringent Lipschitz constraints has proven more difficult than it may seem, evident by the fact that state-of-the-art approach tend more towards \emph{underfitting} than overfitting. Moreover, we posit that a lack of careful exploration of the design space for Lipshitz-based approaches has left potential performance gains on the table. In this work, we provide a more comprehensive evaluation to better uncover the potential of Lipschitz-based certification methods. Using a combination of novel techniques, design optimizations, and synthesis of prior work, we are able to significantly improve the state-of-the-art \emph{verified robust accuracy} (VRA) for deterministic certification on a variety of benchmark datasets, and over a range of perturbation sizes. Of particular note, we discover that the addition of large "Cholesky-orthogonalized residual dense" layers to the end of existing state-of-the-art Lipschitz-controlled ResNet architectures is especially effective for increasing network capacity and performance. Combined with filtered generative data augmentation, our final results further the state of the art deterministic VRA by up to 8.5 percentage points. Code is available at \url{https://github.com/hukkai/liresnet}.

Scaling in Depth: Unlocking Robustness Certification on ImageNet

Notwithstanding the promise of Lipschitz-based approaches to \emph{deterministically} train and certify robust deep networks, the state-of-the-art results only make successful use of feed-forward Convolutional Networks (ConvNets) on low-dimensional data, e.g. CIFAR-10. Because ConvNets often suffer from vanishing gradients when going deep, large-scale datasets with many classes, e.g., ImageNet, have remained out of practical reach. This paper investigates ways to scale up certifiably robust training to Residual Networks (ResNets). First, we introduce the \emph{Linear ResNet} (LiResNet) architecture, which utilizes a new residual block designed to facilitate \emph{tighter} Lipschitz bounds compared to a conventional residual block. Second, we introduce Efficient Margin MAximization (EMMA), a loss function that stabilizes robust training by simultaneously penalizing worst-case adversarial examples from \emph{all} classes. Combining LiResNet and EMMA, we achieve new \emph{state-of-the-art} robust accuracy on CIFAR-10/100 and Tiny-ImageNet under $\ell_2$-norm-bounded perturbations. Moreover, for the first time, we are able to scale up deterministic robustness guarantees to ImageNet, bringing hope to the possibility of applying deterministic certification to real-world applications.

Limitations of Piecewise Linearity for Efficient Robustness Certification

Certified defenses against small-norm adversarial examples have received growing attention in recent years; though certified accuracies of state-of-the-art methods remain far below their non-robust counterparts, despite the fact that benchmark datasets have been shown to be well-separated at far larger radii than the literature generally attempts to certify. In this work, we offer insights that identify potential factors in this performance gap. Specifically, our analysis reveals that piecewise linearity imposes fundamental limitations on the tightness of leading certification techniques. These limitations are felt in practical terms as a greater need for capacity in models hoped to be certified efficiently. Moreover, this is in addition to the capacity necessary to learn a robust boundary, studied in prior work. However, we argue that addressing the limitations of piecewise linearity through scaling up model capacity may give rise to potential difficulties -- particularly regarding robust generalization -- therefore, we conclude by suggesting that developing smooth activation functions may be the way forward for advancing the performance of certified neural networks.

On the Perils of Cascading Robust Classifiers

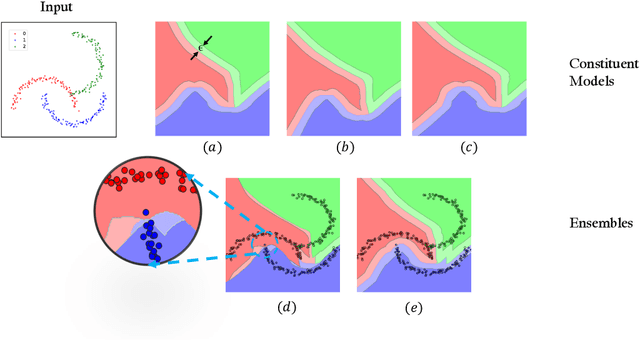
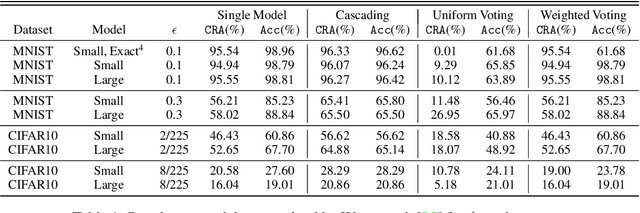
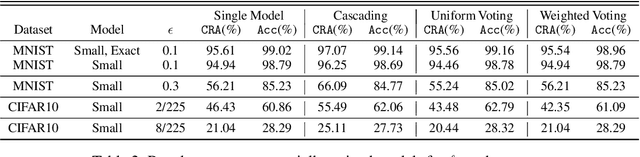
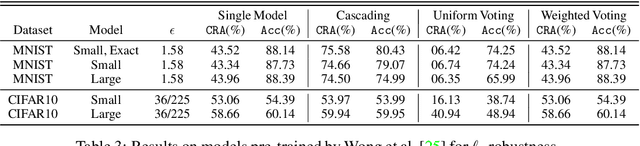
Ensembling certifiably robust neural networks has been shown to be a promising approach for improving the \emph{certified robust accuracy} of neural models. Black-box ensembles that assume only query-access to the constituent models (and their robustness certifiers) during prediction are particularly attractive due to their modular structure. Cascading ensembles are a popular instance of black-box ensembles that appear to improve certified robust accuracies in practice. However, we find that the robustness certifier used by a cascading ensemble is unsound. That is, when a cascading ensemble is certified as locally robust at an input $x$, there can, in fact, be inputs $x'$ in the $\epsilon$-ball centered at $x$, such that the cascade's prediction at $x'$ is different from $x$. We present an alternate black-box ensembling mechanism based on weighted voting which we prove to be sound for robustness certification. Via a thought experiment, we demonstrate that if the constituent classifiers are suitably diverse, voting ensembles can improve certified performance. Our code is available at \url{https://github.com/TristaChi/ensembleKW}.

Selective Ensembles for Consistent Predictions

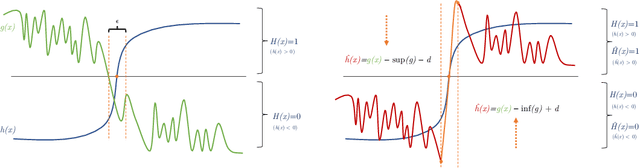
Recent work has shown that models trained to the same objective, and which achieve similar measures of accuracy on consistent test data, may nonetheless behave very differently on individual predictions. This inconsistency is undesirable in high-stakes contexts, such as medical diagnosis and finance. We show that this inconsistent behavior extends beyond predictions to feature attributions, which may likewise have negative implications for the intelligibility of a model, and one's ability to find recourse for subjects. We then introduce selective ensembles to mitigate such inconsistencies by applying hypothesis testing to the predictions of a set of models trained using randomly-selected starting conditions; importantly, selective ensembles can abstain in cases where a consistent outcome cannot be achieved up to a specified confidence level. We prove that that prediction disagreement between selective ensembles is bounded, and empirically demonstrate that selective ensembles achieve consistent predictions and feature attributions while maintaining low abstention rates. On several benchmark datasets, selective ensembles reach zero inconsistently predicted points, with abstention rates as low 1.5%.

Self-Repairing Neural Networks: Provable Safety for Deep Networks via Dynamic Repair

Neural networks are increasingly being deployed in contexts where safety is a critical concern. In this work, we propose a way to construct neural network classifiers that dynamically repair violations of non-relational safety constraints called safe ordering properties. Safe ordering properties relate requirements on the ordering of a network's output indices to conditions on their input, and are sufficient to express most useful notions of non-relational safety for classifiers. Our approach is based on a novel self-repairing layer, which provably yields safe outputs regardless of the characteristics of its input. We compose this layer with an existing network to construct a self-repairing network (SR-Net), and show that in addition to providing safe outputs, the SR-Net is guaranteed to preserve the accuracy of the original network. Notably, our approach is independent of the size and architecture of the network being repaired, depending only on the specified property and the dimension of the network's output; thus it is scalable to large state-of-the-art networks. We show that our approach can be implemented using vectorized computations that execute efficiently on a GPU, introducing run-time overhead of less than one millisecond on current hardware -- even on large, widely-used networks containing hundreds of thousands of neurons and millions of parameters.

Relaxing Local Robustness

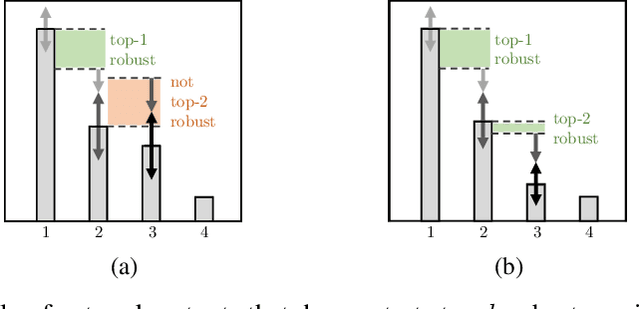
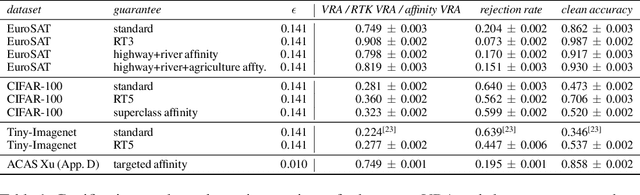
Certifiable local robustness, which rigorously precludes small-norm adversarial examples, has received significant attention as a means of addressing security concerns in deep learning. However, for some classification problems, local robustness is not a natural objective, even in the presence of adversaries; for example, if an image contains two classes of subjects, the correct label for the image may be considered arbitrary between the two, and thus enforcing strict separation between them is unnecessary. In this work, we introduce two relaxed safety properties for classifiers that address this observation: (1) relaxed top-k robustness, which serves as the analogue of top-k accuracy; and (2) affinity robustness, which specifies which sets of labels must be separated by a robustness margin, and which can be $\epsilon$-close in $\ell_p$ space. We show how to construct models that can be efficiently certified against each relaxed robustness property, and trained with very little overhead relative to standard gradient descent. Finally, we demonstrate experimentally that these relaxed variants of robustness are well-suited to several significant classification problems, leading to lower rejection rates and higher certified accuracies than can be obtained when certifying "standard" local robustness.

Globally-Robust Neural Networks

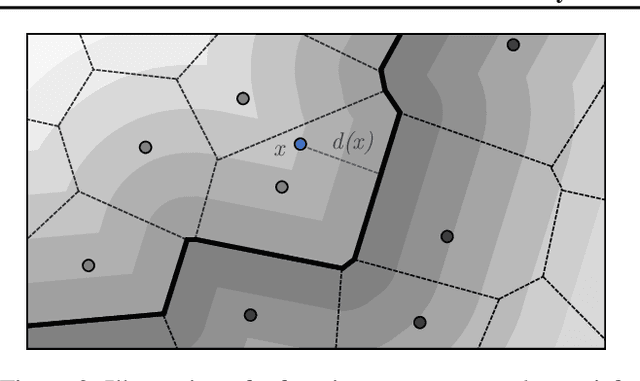
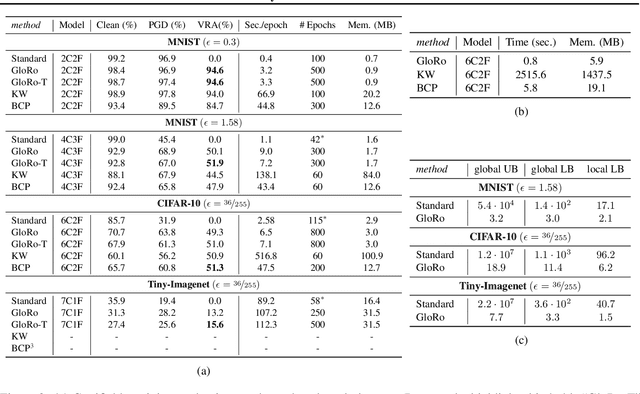
The threat of adversarial examples has motivated work on training certifiably robust neural networks, to facilitate efficient verification of local robustness at inference time. We formalize a notion of global robustness, which captures the operational properties of on-line local robustness certification while yielding a natural learning objective for robust training. We show that widely-used architectures can be easily adapted to this objective by incorporating efficient global Lipschitz bounds into the network, yielding certifiably-robust models by construction that achieve state-of-the-art verifiable and clean accuracy. Notably, this approach requires significantly less time and memory than recent certifiable training methods, and leads to negligible costs when certifying points on-line; for example, our evaluation shows that it is possible to train a large tiny-imagenet model in a matter of hours. We posit that this is possible using inexpensive global bounds -- despite prior suggestions that tighter local bounds are needed for good performance -- because these models are trained to achieve tighter global bounds. Namely, we prove that the maximum achievable verifiable accuracy for a given dataset is not improved by using a local bound.

Influence Paths for Characterizing Subject-Verb Number Agreement in LSTM Language Models

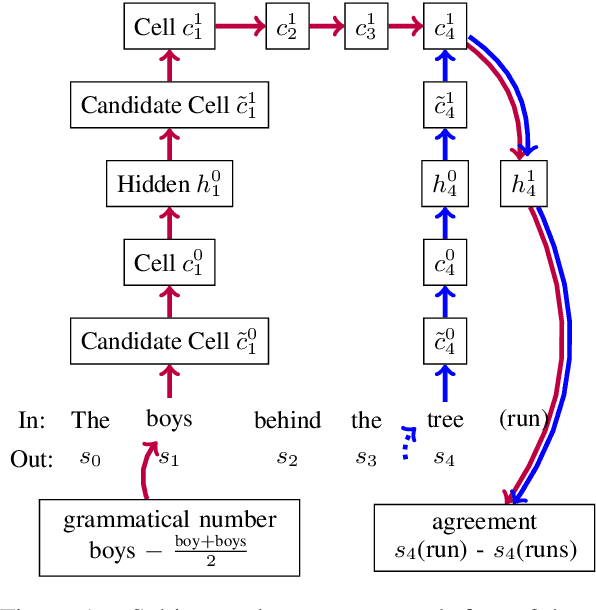
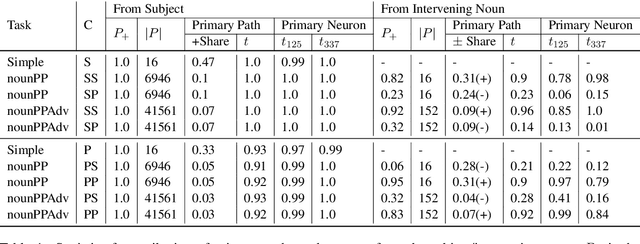
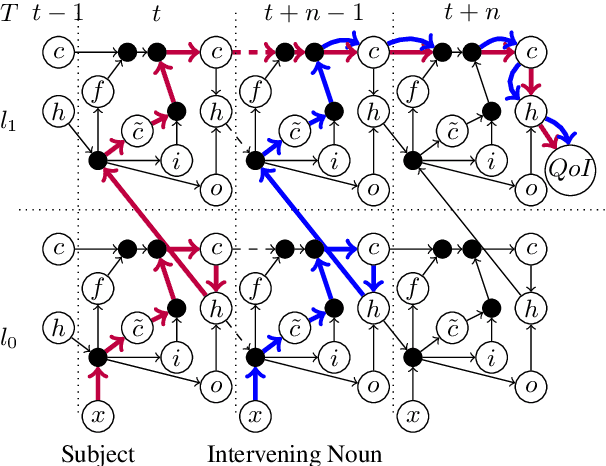
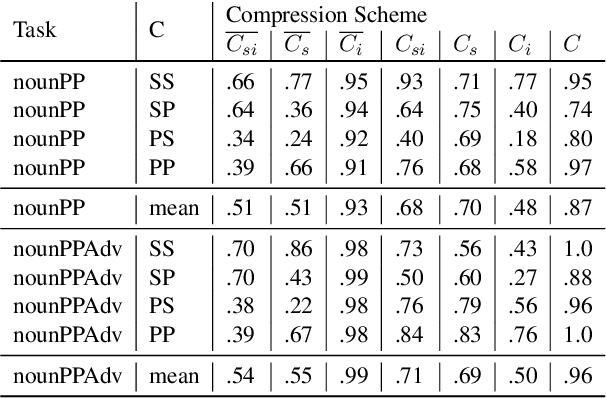
LSTM-based recurrent neural networks are the state-of-the-art for many natural language processing (NLP) tasks. Despite their performance, it is unclear whether, or how, LSTMs learn structural features of natural languages such as subject-verb number agreement in English. Lacking this understanding, the generality of LSTM performance on this task and their suitability for related tasks remains uncertain. Further, errors cannot be properly attributed to a lack of structural capability, training data omissions, or other exceptional faults. We introduce *influence paths*, a causal account of structural properties as carried by paths across gates and neurons of a recurrent neural network. The approach refines the notion of influence (the subject's grammatical number has influence on the grammatical number of the subsequent verb) into a set of gate or neuron-level paths. The set localizes and segments the concept (e.g., subject-verb agreement), its constituent elements (e.g., the subject), and related or interfering elements (e.g., attractors). We exemplify the methodology on a widely-studied multi-layer LSTM language model, demonstrating its accounting for subject-verb number agreement. The results offer both a finer and a more complete view of an LSTM's handling of this structural aspect of the English language than prior results based on diagnostic classifiers and ablation.