Causal Structure Learning for Dynamical Systems with Theoretical Score Analysis

Real world systems evolve in continuous-time according to their underlying causal relationships, yet their dynamics are often unknown. Existing approaches to learning such dynamics typically either discretize time -- leading to poor performance on irregularly sampled data -- or ignore the underlying causality. We propose CaDyT, a novel method for causal discovery on dynamical systems addressing both these challenges. In contrast to state-of-the-art causal discovery methods that model the problem using discrete-time Dynamic Bayesian networks, our formulation is grounded in Difference-based causal models, which allow milder assumptions for modeling the continuous nature of the system. CaDyT leverages exact Gaussian Process inference for modeling the continuous-time dynamics which is more aligned with the underlying dynamical process. We propose a practical instantiation that identifies the causal structure via a greedy search guided by the Algorithmic Markov Condition and Minimum Description Length principle. Our experiments show that CaDyT outperforms state-of-the-art methods on both regularly and irregularly-sampled data, discovering causal networks closer to the true underlying dynamics.

Safe Active Learning for Gaussian Differential Equations

Gaussian Process differential equations (GPODE) have recently gained momentum due to their ability to capture dynamics behavior of systems and also represent uncertainty in predictions. Prior work has described the process of training the hyperparameters and, thereby, calibrating GPODE to data. How to design efficient algorithms to collect data for training GPODE models is still an open field of research. Nevertheless high-quality training data is key for model performance. Furthermore, data collection leads to time-cost and financial-cost and might in some areas even be safety critical to the system under test. Therefore, algorithms for safe and efficient data collection are central for building high quality GPODE models. Our novel Safe Active Learning (SAL) for GPODE algorithm addresses this challenge by suggesting a mechanism to propose efficient and non-safety-critical data to collect. SAL GPODE does so by sequentially suggesting new data, measuring it and updating the GPODE model with the new data. In this way, subsequent data points are iteratively suggested. The core of our SAL GPODE algorithm is a constrained optimization problem maximizing information of new data for GPODE model training constrained by the safety of the underlying system. We demonstrate our novel SAL GPODE's superiority compared to a standard, non-active way of measuring new data on two relevant examples.

Learning Hybrid Dynamics Models With Simulator-Informed Latent States

Dynamics model learning deals with the task of inferring unknown dynamics from measurement data and predicting the future behavior of the system. A typical approach to address this problem is to train recurrent models. However, predictions with these models are often not physically meaningful. Further, they suffer from deteriorated behavior over time due to accumulating errors. Often, simulators building on first principles are available being physically meaningful by design. However, modeling simplifications typically cause inaccuracies in these models. Consequently, hybrid modeling is an emerging trend that aims to combine the best of both worlds. In this paper, we propose a new approach to hybrid modeling, where we inform the latent states of a learned model via a black-box simulator. This allows to control the predictions via the simulator preventing them from accumulating errors. This is especially challenging since, in contrast to previous approaches, access to the simulator's latent states is not available. We tackle the task by leveraging observers, a well-known concept from control theory, inferring unknown latent states from observations and dynamics over time. In our learning-based setting, we jointly learn the dynamics and an observer that infers the latent states via the simulator. Thus, the simulator constantly corrects the latent states, compensating for modeling mismatch caused by learning. To maintain flexibility, we train an RNN-based residuum for the latent states that cannot be informed by the simulator.

Exact Inference for Continuous-Time Gaussian Process Dynamics

Physical systems can often be described via a continuous-time dynamical system. In practice, the true system is often unknown and has to be learned from measurement data. Since data is typically collected in discrete time, e.g. by sensors, most methods in Gaussian process (GP) dynamics model learning are trained on one-step ahead predictions. This can become problematic in several scenarios, e.g. if measurements are provided at irregularly-sampled time steps or physical system properties have to be conserved. Thus, we aim for a GP model of the true continuous-time dynamics. Higher-order numerical integrators provide the necessary tools to address this problem by discretizing the dynamics function with arbitrary accuracy. Many higher-order integrators require dynamics evaluations at intermediate time steps making exact GP inference intractable. In previous work, this problem is often tackled by approximating the GP posterior with variational inference. However, exact GP inference is preferable in many scenarios, e.g. due to its mathematical guarantees. In order to make direct inference tractable, we propose to leverage multistep and Taylor integrators. We demonstrate how to derive flexible inference schemes for these types of integrators. Further, we derive tailored sampling schemes that allow to draw consistent dynamics functions from the learned posterior. This is crucial to sample consistent predictions from the dynamics model. We demonstrate empirically and theoretically that our approach yields an accurate representation of the continuous-time system.

Combining Slow and Fast: Complementary Filtering for Dynamics Learning

Modeling an unknown dynamical system is crucial in order to predict the future behavior of the system. A standard approach is training recurrent models on measurement data. While these models typically provide exact short-term predictions, accumulating errors yield deteriorated long-term behavior. In contrast, models with reliable long-term predictions can often be obtained, either by training a robust but less detailed model, or by leveraging physics-based simulations. In both cases, inaccuracies in the models yield a lack of short-time details. Thus, different models with contrastive properties on different time horizons are available. This observation immediately raises the question: Can we obtain predictions that combine the best of both worlds? Inspired by sensor fusion tasks, we interpret the problem in the frequency domain and leverage classical methods from signal processing, in particular complementary filters. This filtering technique combines two signals by applying a high-pass filter to one signal, and low-pass filtering the other. Essentially, the high-pass filter extracts high-frequencies, whereas the low-pass filter extracts low frequencies. Applying this concept to dynamics model learning enables the construction of models that yield accurate long- and short-term predictions. Here, we propose two methods, one being purely learning-based and the other one being a hybrid model that requires an additional physics-based simulator.

Symplectic Gaussian Process Dynamics

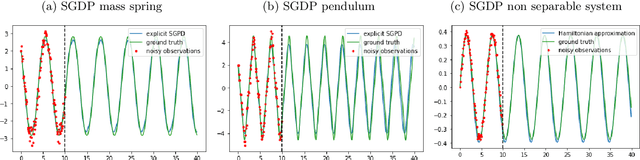
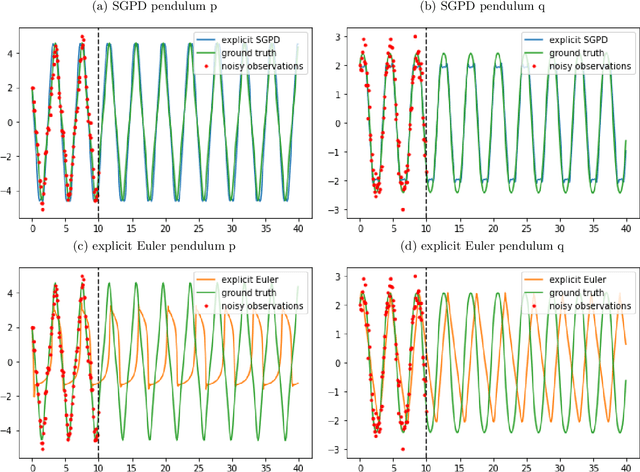
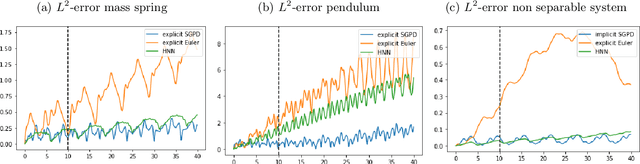
Dynamics model learning is challenging and at the same time an active field of research. Due to potential safety critical downstream applications, such as control tasks, there is a need for theoretical guarantees. While GPs induce rich theoretical guarantees as function approximators in space, they do not explicitly cope with the time aspect of dynamical systems. However, propagating system properties through time is exactly what classical numerical integrators were designed for. We introduce a recurrent sparse Gaussian process based variational inference scheme that is able to discretize the underlying system with any explicit or implicit single or multistep integrator, thus leveraging properties of numerical integrators. In particular we discuss Hamiltonian problems coupled with symplectic integrators producing volume preserving predictions.