Distinguish Confusing Law Articles for Legal Judgment Prediction

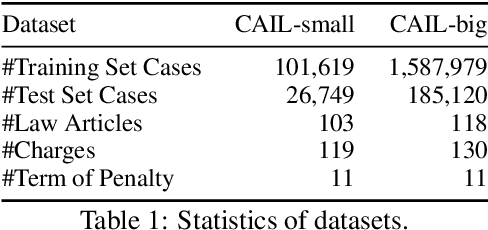
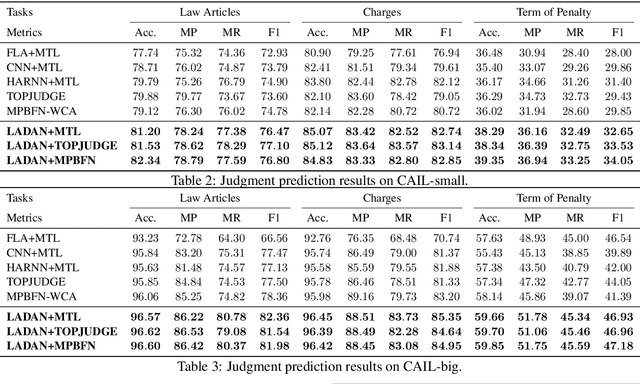
Legal Judgment Prediction (LJP) is the task of automatically predicting a law case's judgment results given a text describing its facts, which has excellent prospects in judicial assistance systems and convenient services for the public. In practice, confusing charges are frequent, because law cases applicable to similar law articles are easily misjudged. For addressing this issue, the existing method relies heavily on domain experts, which hinders its application in different law systems. In this paper, we present an end-to-end model, LADAN, to solve the task of LJP. To distinguish confusing charges, we propose a novel graph neural network to automatically learn subtle differences between confusing law articles and design a novel attention mechanism that fully exploits the learned differences to extract compelling discriminative features from fact descriptions attentively. Experiments conducted on real-world datasets demonstrate the superiority of our LADAN.

Fast Generating A Large Number of Gumbel-Max Variables

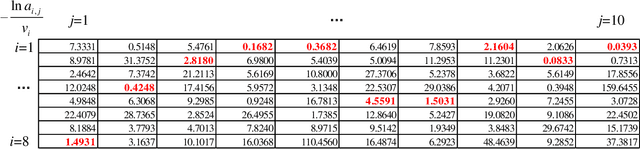
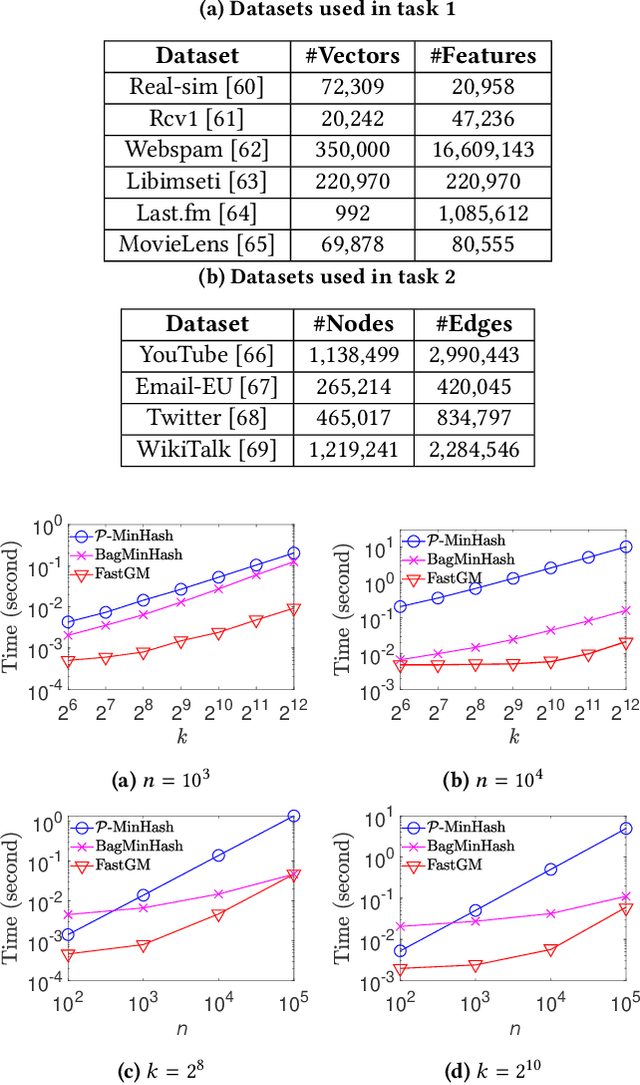
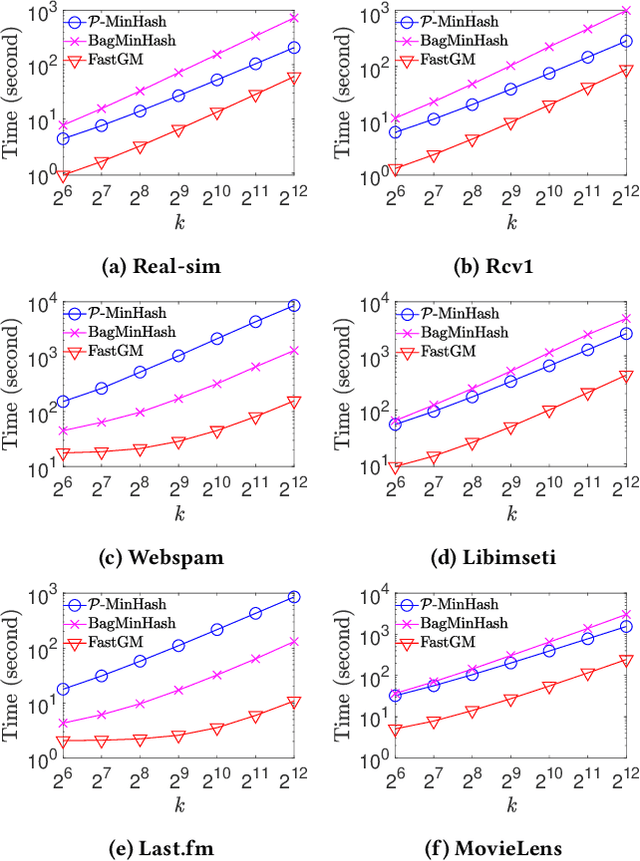
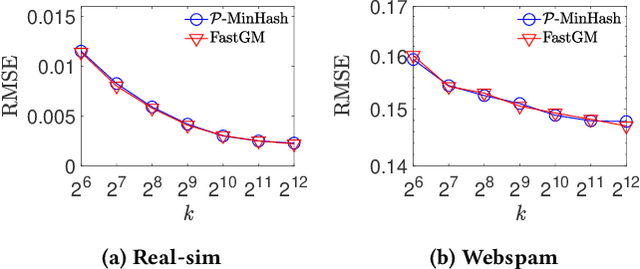
The well-known Gumbel-Max Trick for sampling elements from a categorical distribution (or more generally a nonnegative vector) and its variants have been widely used in areas such as machine learning and information retrieval. To sample a random element $i$ (or a Gumbel-Max variable $i$) in proportion to its positive weight $v_i$, the Gumbel-Max Trick first computes a Gumbel random variable $g_i$ for each positive weight element $i$, and then samples the element $i$ with the largest value of $g_i+\ln v_i$. Recently, applications including similarity estimation and graph embedding require to generate $k$ independent Gumbel-Max variables from high dimensional vectors. However, it is computationally expensive for a large $k$ (e.g., hundreds or even thousands) when using the traditional Gumbel-Max Trick. To solve this problem, we propose a novel algorithm, \emph{FastGM}, that reduces the time complexity from $O(kn^+)$ to $O(k \ln k + n^+)$, where $n^+$ is the number of positive elements in the vector of interest. Instead of computing $k$ independent Gumbel random variables directly, we find that there exists a technique to generate these variables in descending order. Using this technique, our method FastGM computes variables $g_i+\ln v_i$ for all positive elements $i$ in descending order. As a result, FastGM significantly reduces the computation time because we can stop the procedure of Gumbel random variables computing for many elements especially for those with small weights. Experiments on a variety of real-world datasets show that FastGM is orders of magnitude faster than state-of-the-art methods without sacrificing accuracy and incurring additional expenses.

MR-GNN: Multi-Resolution and Dual Graph Neural Network for Predicting Structured Entity Interactions

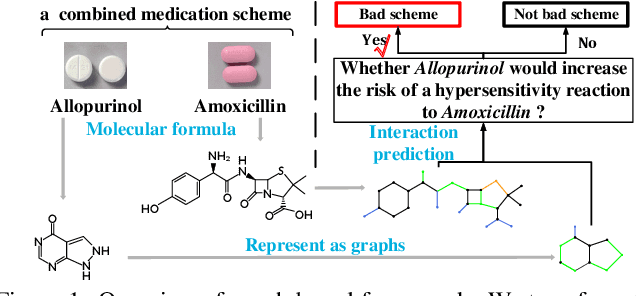
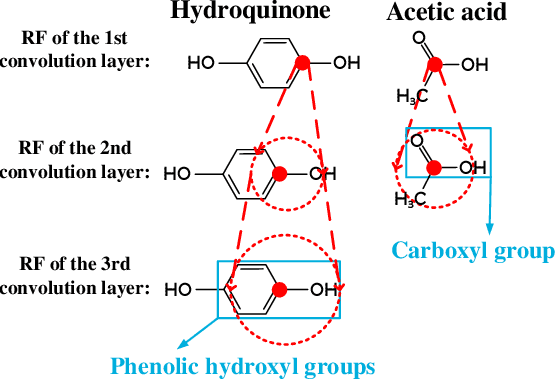
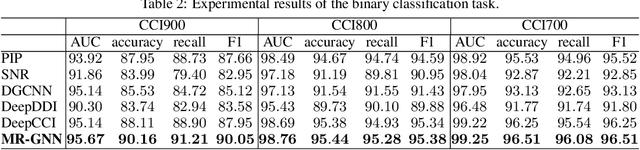
Predicting interactions between structured entities lies at the core of numerous tasks such as drug regimen and new material design. In recent years, graph neural networks have become attractive. They represent structured entities as graphs and then extract features from each individual graph using graph convolution operations. However, these methods have some limitations: i) their networks only extract features from a fix-sized subgraph structure (i.e., a fix-sized receptive field) of each node, and ignore features in substructures of different sizes, and ii) features are extracted by considering each entity independently, which may not effectively reflect the interaction between two entities. To resolve these problems, we present MR-GNN, an end-to-end graph neural network with the following features: i) it uses a multi-resolution based architecture to extract node features from different neighborhoods of each node, and, ii) it uses dual graph-state long short-term memory networks (L-STMs) to summarize local features of each graph and extracts the interaction features between pairwise graphs. Experiments conducted on real-world datasets show that MR-GNN improves the prediction of state-of-the-art methods.

On Analyzing Estimation Errors due to Constrained Connections in Online Review Systems

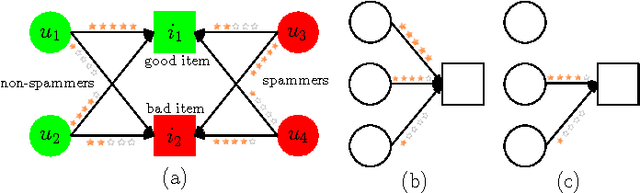
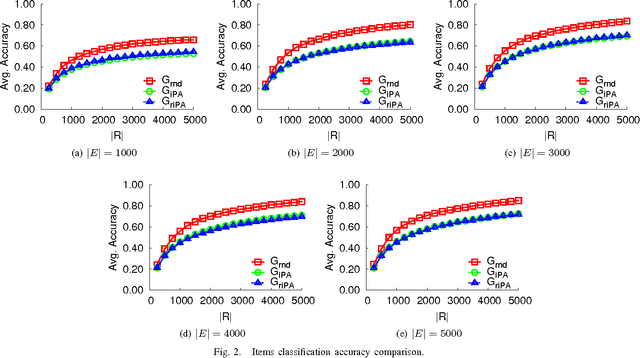
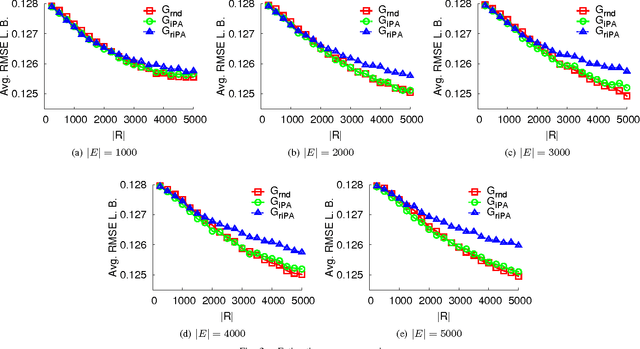
Constrained connection is the phenomenon that a reviewer can only review a subset of products/services due to narrow range of interests or limited attention capacity. In this work, we study how constrained connections can affect estimation performance in online review systems (ORS). We find that reviewers' constrained connections will cause poor estimation performance, both from the measurements of estimation accuracy and Bayesian Cramer Rao lower bound.