Phase Retrieval using Single-Instance Deep Generative Prior

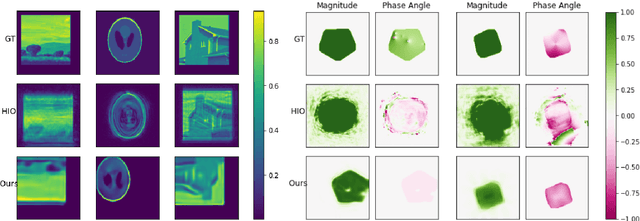
Several deep learning methods for phase retrieval exist, but most of them fail on realistic data without precise support information. We propose a novel method based on single-instance deep generative prior that works well on complex-valued crystal data.

Rethink Transfer Learning in Medical Image Classification

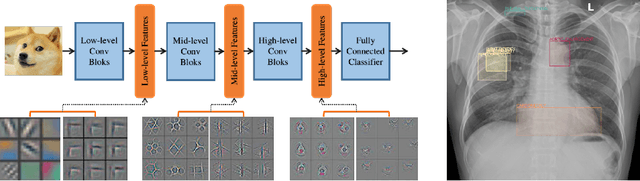
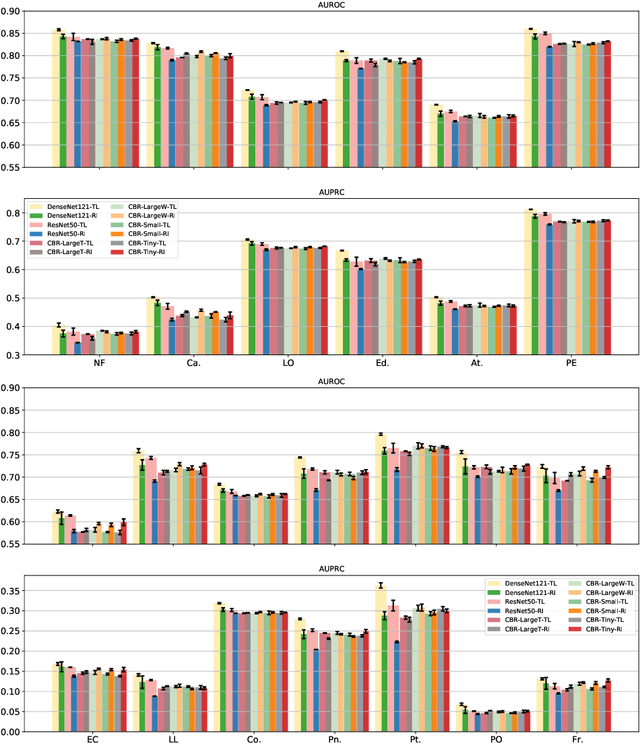
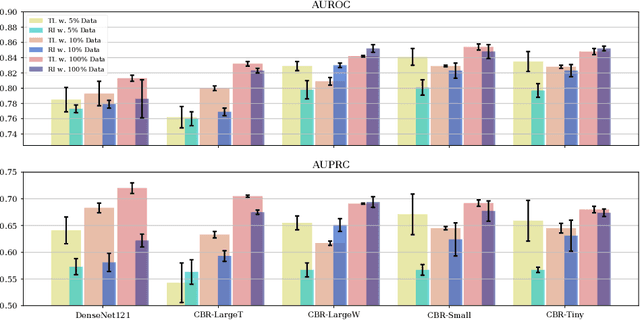
Transfer learning (TL) with deep convolutional neural networks (DCNNs) has proved successful in medical image classification (MIC). However, the current practice is puzzling, as MIC typically relies only on low- and/or mid-level features that are learned in the bottom layers of DCNNs. Following this intuition, we question the current strategies of TL in MIC. In this paper, we perform careful experimental comparisons between shallow and deep networks for classification on two chest x-ray datasets, using different TL strategies. We find that deep models are not always favorable, and finetuning truncated deep models almost always yields the best performance, especially in data-poor regimes. Project webpage: https://sun-umn.github.io/Transfer-Learning-in-Medical-Imaging/ Keywords: Transfer learning, Medical image classification, Feature hierarchy, Medical imaging, Evaluation metrics, Imbalanced data

A Prospective Observational Study to Investigate Performance of a Chest X-ray Artificial Intelligence Diagnostic Support Tool Across 12 U.S. Hospitals

Importance: An artificial intelligence (AI)-based model to predict COVID-19 likelihood from chest x-ray (CXR) findings can serve as an important adjunct to accelerate immediate clinical decision making and improve clinical decision making. Despite significant efforts, many limitations and biases exist in previously developed AI diagnostic models for COVID-19. Utilizing a large set of local and international CXR images, we developed an AI model with high performance on temporal and external validation. Conclusions and Relevance: AI-based diagnostic tools may serve as an adjunct, but not replacement, for clinical decision support of COVID-19 diagnosis, which largely hinges on exposure history, signs, and symptoms. While AI-based tools have not yet reached full diagnostic potential in COVID-19, they may still offer valuable information to clinicians taken into consideration along with clinical signs and symptoms.

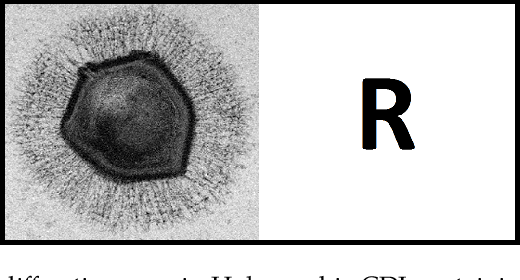
Towards Low-Photon Nanoscale Imaging: Holographic Phase Retrieval via Maximum Likelihood Optimization

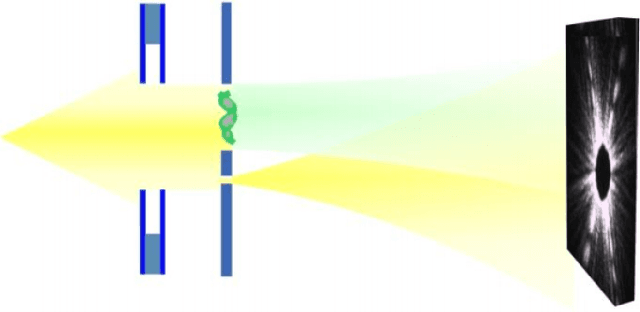
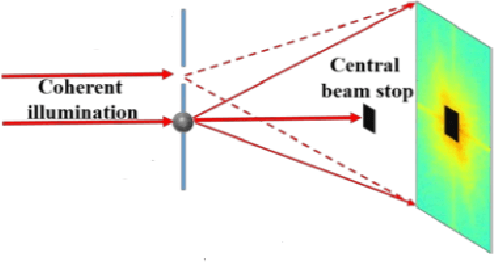
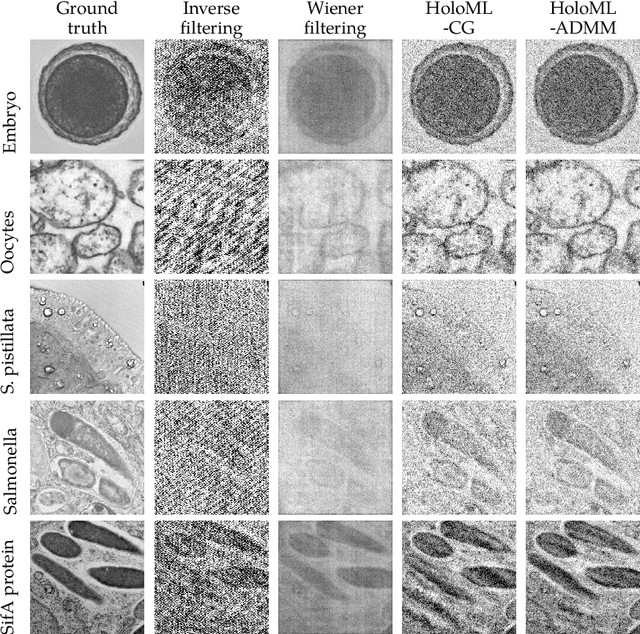
A new algorithmic framework is presented for holographic phase retrieval via maximum likelihood optimization, which allows for practical and robust image reconstruction. This framework is especially well-suited for holographic coherent diffraction imaging in the \textit{low-photon regime}, where data is highly corrupted by Poisson shot noise. Thus, this methodology provides a viable solution towards the advent of \textit{low-photon nanoscale imaging}, which is a fundamental challenge facing the current state of imaging technologies. Practical optimization algorithms are derived and implemented, and extensive numerical simulations demonstrate significantly improved image reconstruction versus the leading algorithms currently in use. Further experiments compare the performance of popular holographic reference geometries to determine the optimal combined physical setup and algorithm pipeline for practical implementation. Additional features of these methods are also demonstrated, which allow for fewer experimental constraints.

Inverse Problems, Deep Learning, and Symmetry Breaking

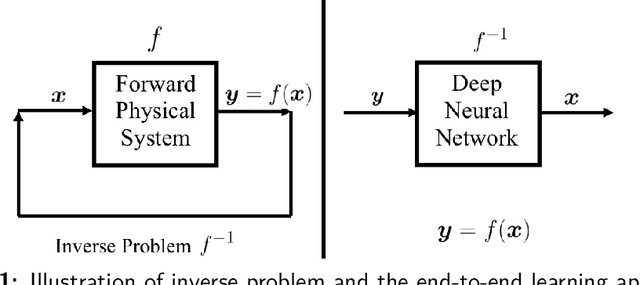
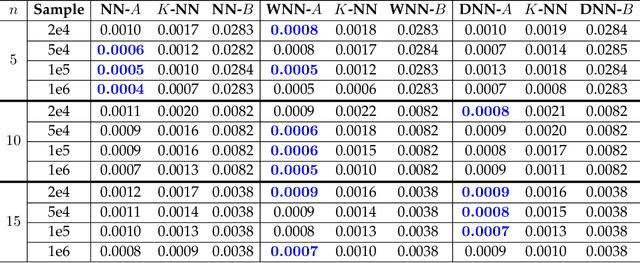
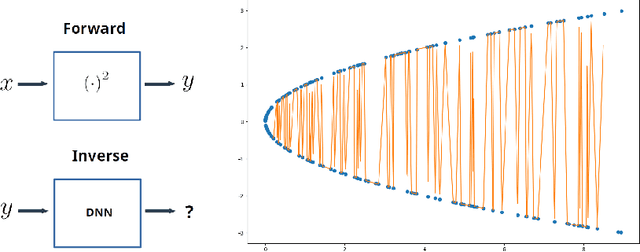
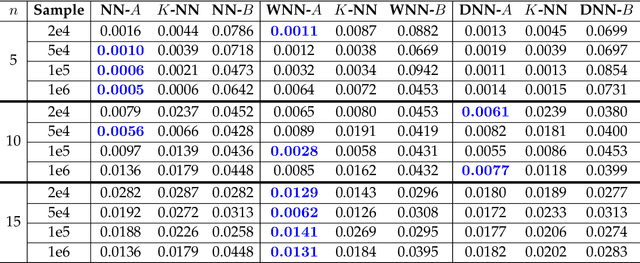
In many physical systems, inputs related by intrinsic system symmetries are mapped to the same output. When inverting such systems, i.e., solving the associated inverse problems, there is no unique solution. This causes fundamental difficulties for deploying the emerging end-to-end deep learning approach. Using the generalized phase retrieval problem as an illustrative example, we show that careful symmetry breaking on the training data can help get rid of the difficulties and significantly improve the learning performance. We also extract and highlight the underlying mathematical principle of the proposed solution, which is directly applicable to other inverse problems.

Dual-Reference Design for Holographic Coherent Diffraction Imaging

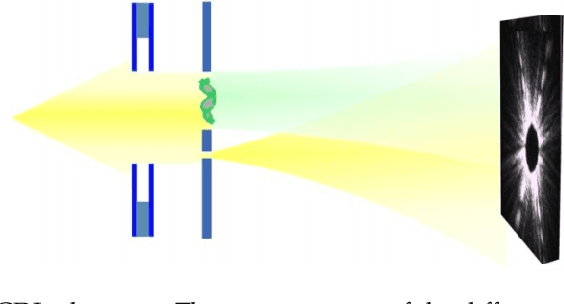
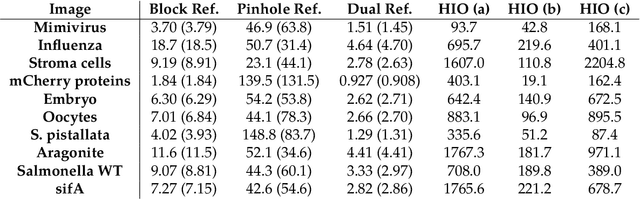
A new reference design is introduced for Holographic Coherent Diffraction Imaging. This consists of two reference portions - being "block" and "pinhole" shaped regions - adjacent to the imaging specimen. Expected error analysis on data following a Poisson shot noise model shows that the dual-reference scheme produces smaller weighting of error across the frequency spectrum than does the leading single-reference schemes. Numerical experiments on simulated data also shows the dual-reference scheme achieving a smaller recovery error than the leading single-reference schemes.

Subgradient Descent Learns Orthogonal Dictionaries

This paper concerns dictionary learning, i.e., sparse coding, a fundamental representation learning problem. We show that a subgradient descent algorithm, with random initialization, can provably recover orthogonal dictionaries on a natural nonsmooth, nonconvex $\ell_1$ minimization formulation of the problem, under mild statistical assumptions on the data. This is in contrast to previous provable methods that require either expensive computation or delicate initialization schemes. Our analysis develops several tools for characterizing landscapes of nonsmooth functions, which might be of independent interest for provable training of deep networks with nonsmooth activations (e.g., ReLU), among numerous other applications. Preliminary experiments corroborate our analysis and show that our algorithm works well empirically in recovering orthogonal dictionaries.

Dictionary Learning in Fourier Transform Scanning Tunneling Spectroscopy

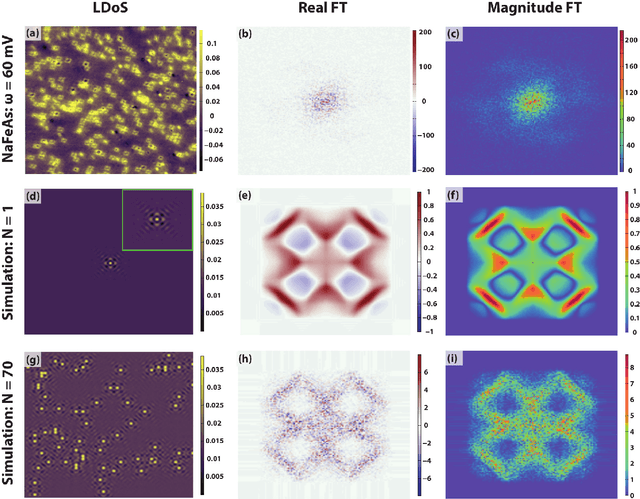
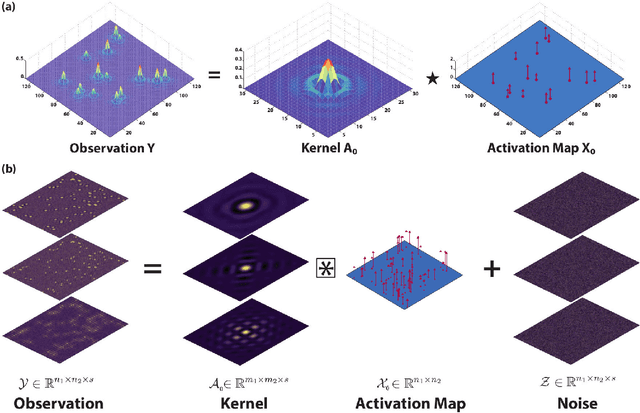
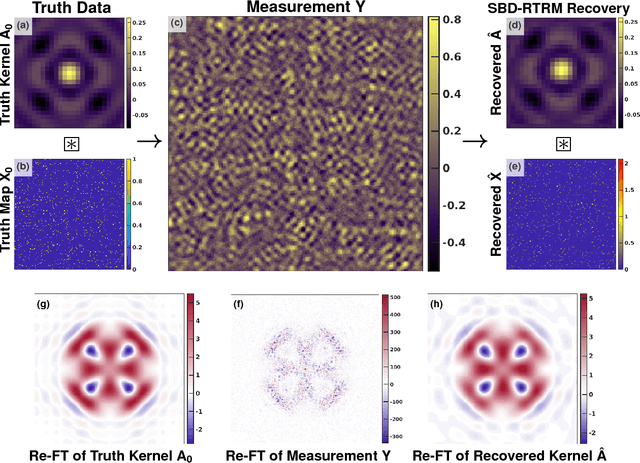
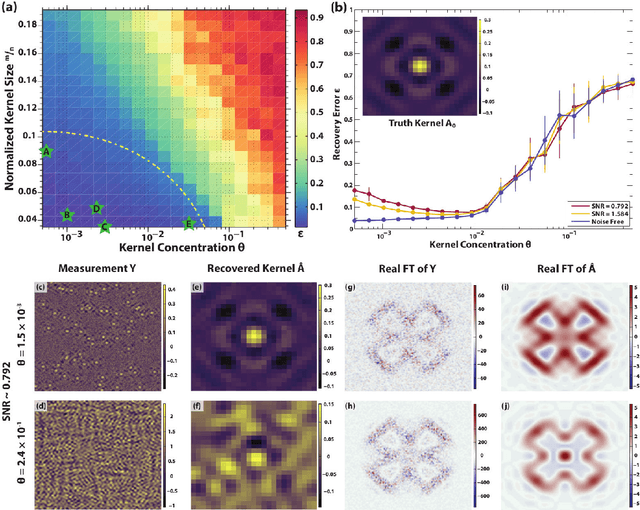
Modern high-resolution microscopes, such as the scanning tunneling microscope, are commonly used to study specimens that have dense and aperiodic spatial structure. Extracting meaningful information from images obtained from such microscopes remains a formidable challenge. Fourier analysis is commonly used to analyze the underlying structure of fundamental motifs present in an image. However, the Fourier transform fundamentally suffers from severe phase noise when applied to aperiodic images. Here, we report the development of a new algorithm based on nonconvex optimization, applicable to any microscopy modality, that directly uncovers the fundamental motifs present in a real-space image. Apart from being quantitatively superior to traditional Fourier analysis, we show that this novel algorithm also uncovers phase sensitive information about the underlying motif structure. We demonstrate its usefulness by studying scanning tunneling microscopy images of a Co-doped iron arsenide superconductor and prove that the application of the algorithm allows for the complete recovery of quasiparticle interference in this material. Our phase sensitive quasiparticle interference imaging results indicate that the pairing symmetry in optimally doped NaFeAs is consistent with a sign-changing s+- order parameter.

A Local Analysis of Block Coordinate Descent for Gaussian Phase Retrieval

While convergence of the Alternating Direction Method of Multipliers (ADMM) on convex problems is well studied, convergence on nonconvex problems is only partially understood. In this paper, we consider the Gaussian phase retrieval problem, formulated as a linear constrained optimization problem with a biconvex objective. The particular structure allows for a novel application of the ADMM. It can be shown that the dual variable is zero at the global minimizer. This motivates the analysis of a block coordinate descent algorithm, which is equivalent to the ADMM with the dual variable fixed to be zero. We show that the block coordinate descent algorithm converges to the global minimizer at a linear rate, when starting from a deterministically achievable initialization point.

A Geometric Analysis of Phase Retrieval

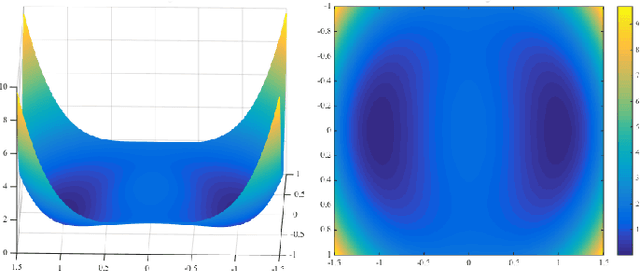
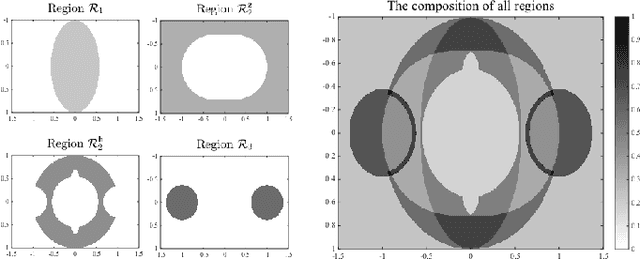
Can we recover a complex signal from its Fourier magnitudes? More generally, given a set of $m$ measurements, $y_k = |\mathbf a_k^* \mathbf x|$ for $k = 1, \dots, m$, is it possible to recover $\mathbf x \in \mathbb{C}^n$ (i.e., length-$n$ complex vector)? This **generalized phase retrieval** (GPR) problem is a fundamental task in various disciplines, and has been the subject of much recent investigation. Natural nonconvex heuristics often work remarkably well for GPR in practice, but lack clear theoretical explanations. In this paper, we take a step towards bridging this gap. We prove that when the measurement vectors $\mathbf a_k$'s are generic (i.i.d. complex Gaussian) and the number of measurements is large enough ($m \ge C n \log^3 n$), with high probability, a natural least-squares formulation for GPR has the following benign geometric structure: (1) there are no spurious local minimizers, and all global minimizers are equal to the target signal $\mathbf x$, up to a global phase; and (2) the objective function has a negative curvature around each saddle point. This structure allows a number of iterative optimization methods to efficiently find a global minimizer, without special initialization. To corroborate the claim, we describe and analyze a second-order trust-region algorithm.