Theory and Algorithms for Pulse Signal Processing

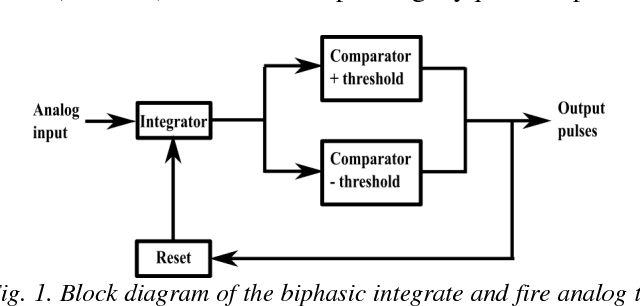
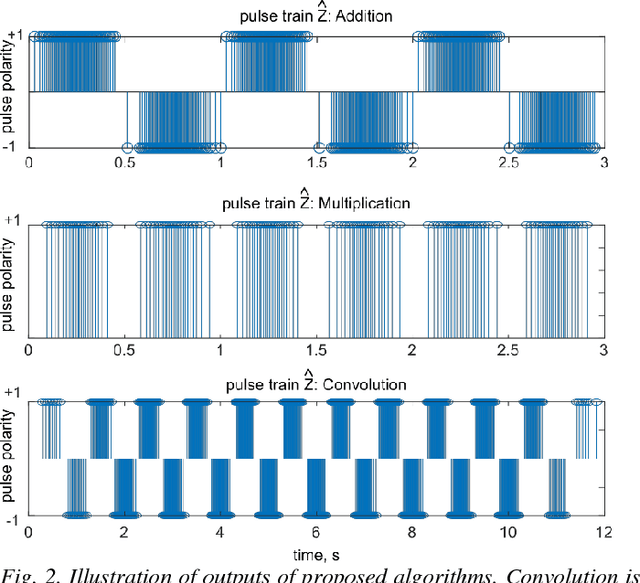
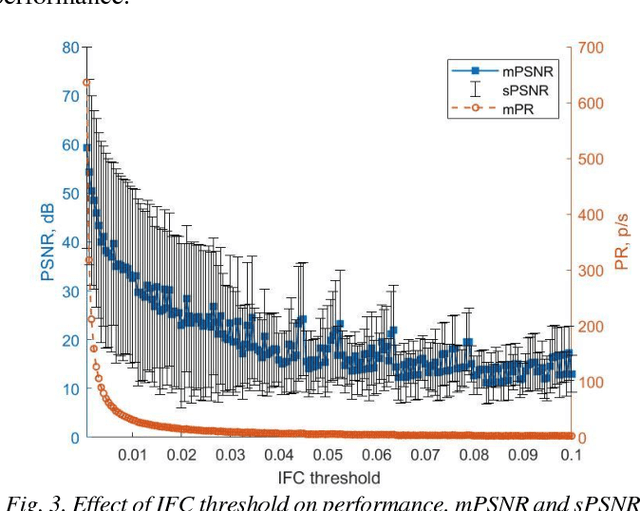
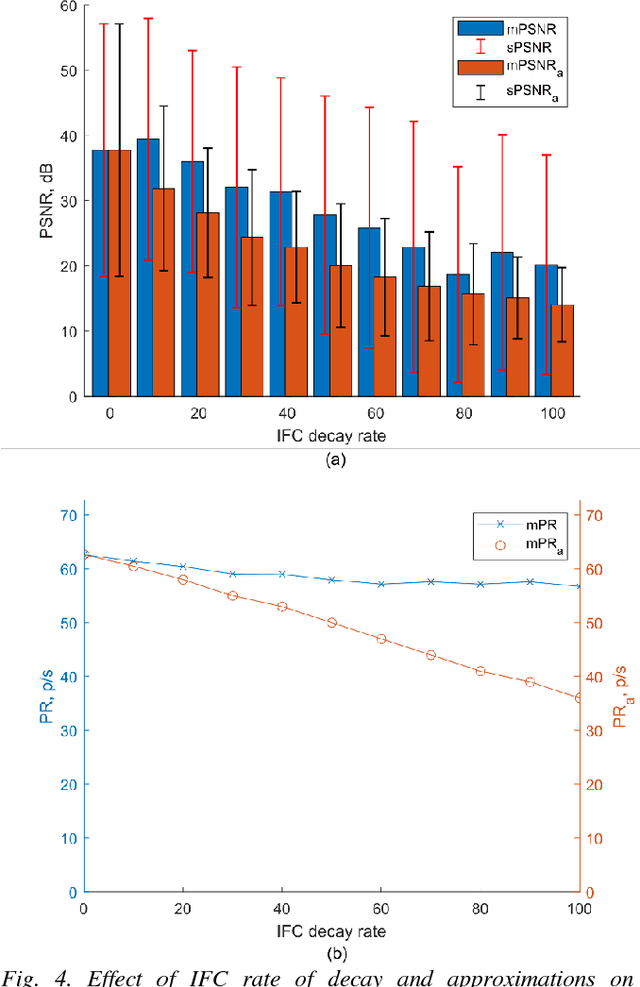
The integrate and fire converter transforms an analog signal into train of biphasic pulses. The pulse train has information encoded in the timing and polarity of pulses. While it has been shown that any finite bandwidth analog signal can be reconstructed from these pulse trains with an error as small as desired, there is a need for fundamental signal processing techniques to operate directly on pulse trains without signal reconstruction. In this paper, the feasibility of performing online the signal processing operations of addition, multiplication, and convolution of analog signals using their pulses train representations is explored. Theoretical framework to perform signal processing with pulse trains imposing minimal restrictions is derived, and algorithms for online implementation of the operators are developed. Performance of the algorithms in processing simulated data is studied. An application of noise subtraction and representation of relevant features of interest in electrocardiogram signal is demonstrated with mean pulse rate less than 20 pulses per second.

Simple stopping criteria for information theoretic feature selection

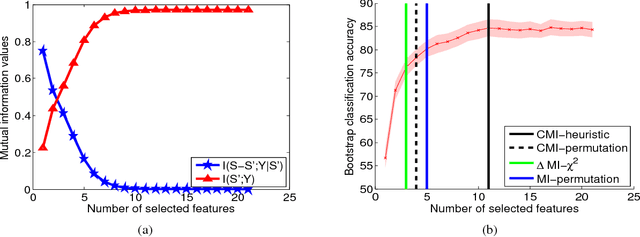
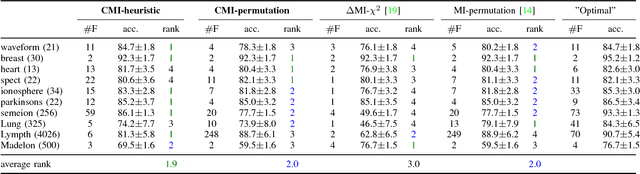
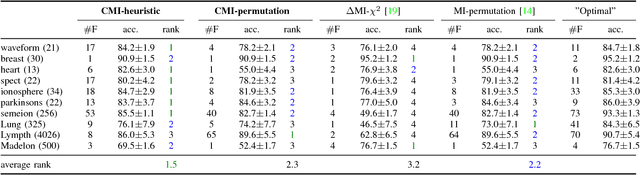
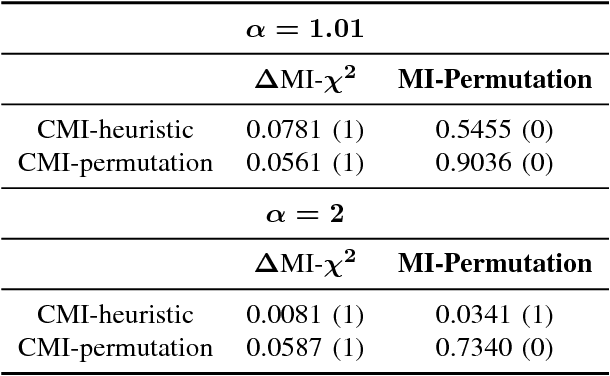
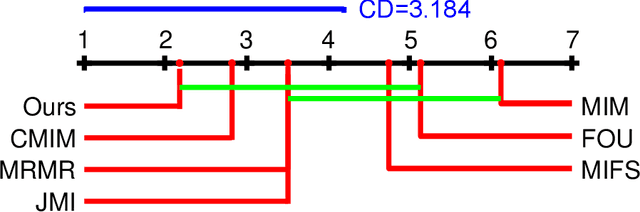
Information theoretic feature selection aims to select a smallest feature subset such that the mutual information between the selected features and the class labels is maximized. Despite the simplicity of this objective, there still remains several open problems to optimize it. These include, for example, the automatic determination of the optimal subset size (i.e., the number of features) or a stopping criterion if the greedy searching strategy is adopted. In this letter, we suggest two stopping criteria by just monitoring the conditional mutual information (CMI) among groups of variables. Using the recently developed multivariate matrix-based Renyi's \alpha-entropy functional, we show that the CMI among groups of variables can be easily estimated without any decomposition or approximation, hence making our criteria easily implemented and seamlessly integrated into any existing information theoretic feature selection methods with greedy search strategy.

Understanding Convolutional Neural Network Training with Information Theory

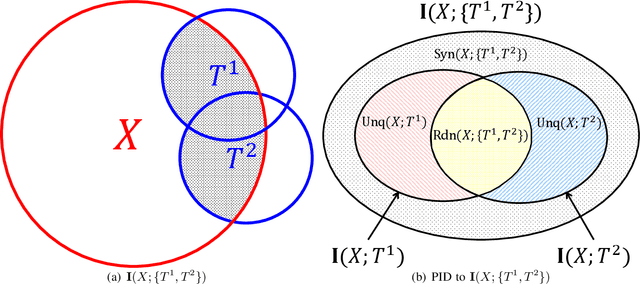
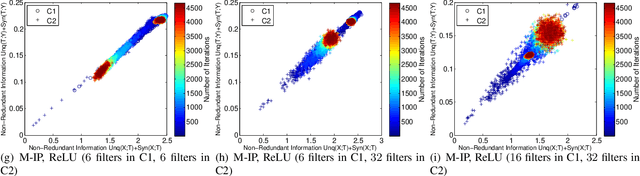
Using information theoretic concepts to understand and explore the inner organization of deep neural networks (DNNs) remains a big challenge. Recently, the concept of an information plane (coupled with the famed information bottleneck principle) began to shed light on the analysis of multilayer perceptrons (MLPs). We provided an in-depth insight into stacked autoencoders (SAEs) using a novel matrix-based Renyi's {\alpha}-entropy functional, enabling for the first time the analysis of the dynamics of learning using information flow in the real-world scenario involving complex network architecture and large data. Despite the great potential of these past works, there are several open questions when it comes to applying information theoretic concepts to understand convolutional neural networks (CNNs). These include for instance the accurate estimation of information quantities among multiple variables, and the many different training methodologies. By extending the novel matrix-based Renyi's {\alpha}-entropy functional to a multivariate scenario and introducing the partial information decomposition (PID) framework, this paper presents a systematic method to analyze CNNs training using information theory. Our results validate two fundamental data processing inequalities in CNNs, and also reveals some fundamental issues embedded in the training phase of CNNs.

Understanding Autoencoders with Information Theoretic Concepts

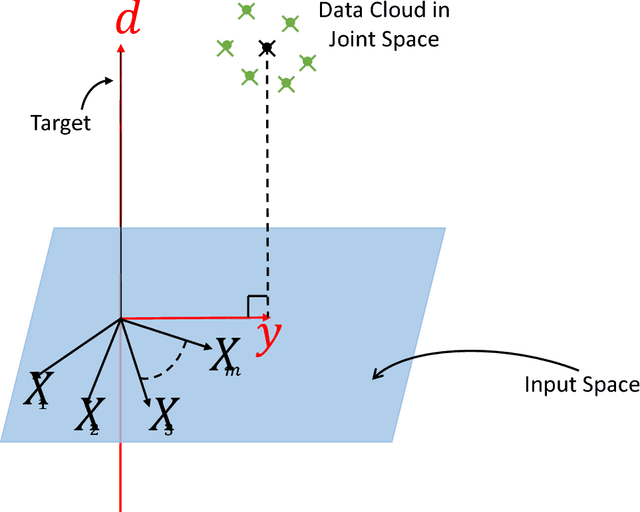
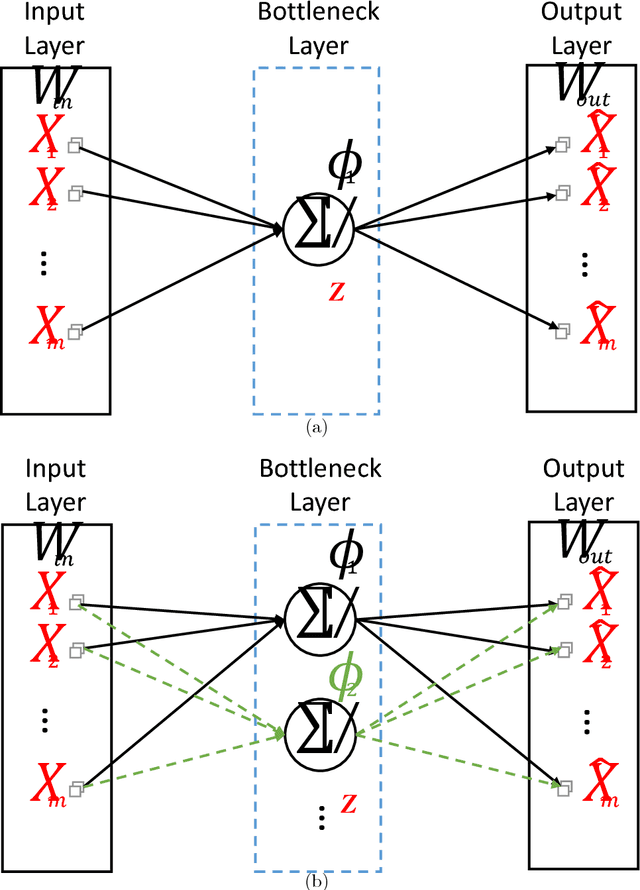
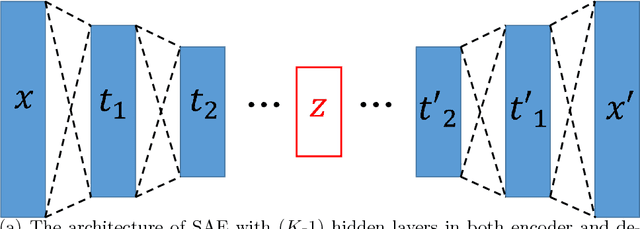
Despite their great success in practical applications, there is still a lack of theoretical and systematic methods to analyze deep neural networks. In this paper, we illustrate an advanced information theoretic methodology to understand the dynamics of learning and the design of autoencoders, a special type of deep learning architectures that resembles a communication channel. By generalizing the information plane to any cost function, and inspecting the roles and dynamics of different layers using layer-wise information quantities, we emphasize the role that mutual information plays in quantifying learning from data. We further suggest and also experimentally validate, for mean square error training, three fundamental properties regarding the layer-wise flow of information and intrinsic dimensionality of the bottleneck layer, using respectively the data processing inequality and the identification of a bifurcation point in the information plane that is controlled by the given data. Our observations have direct impact on the optimal design of autoencoders, the design of alternative feedforward training methods, and even in the problem of generalization.

Multivariate Extension of Matrix-based Renyi's α-order Entropy Functional

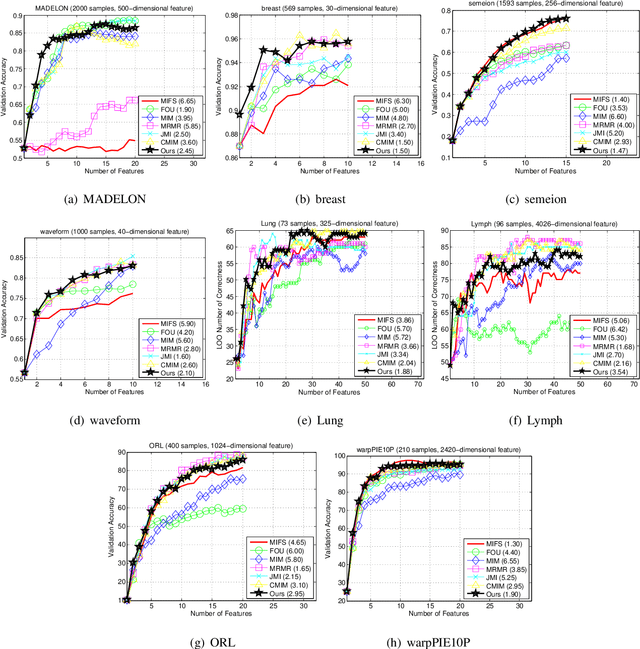
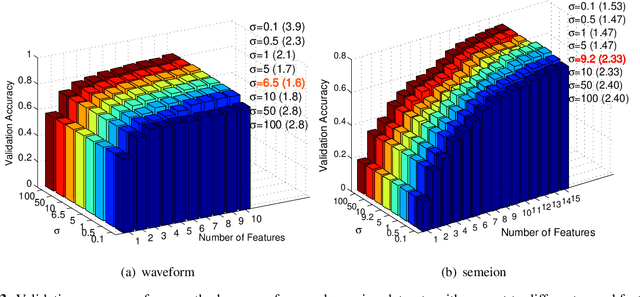
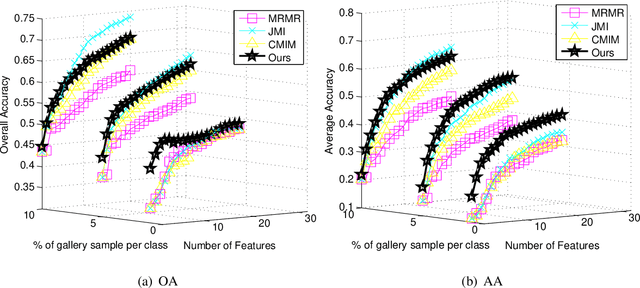
The matrix-based Renyi's {\alpha}-order entropy functional was recently introduced using the normalized eigenspectrum of an Hermitian matrix of the projected data in the reproducing kernel Hilbert space (RKHS). However, the current theory in the matrix-based Renyi's {\alpha}-order entropy functional only defines the entropy of a single variable or mutual information between two random variables. In information theory and machine learning communities, one is also frequently interested in multivariate information quantities, such as the multivariate joint entropy and different interactive quantities among multiple variables. In this paper, we first define the matrix-based Renyi's {\alpha}-order joint entropy among multiple variables. We then show how this definition can ease the estimation of various information quantities that measure the interactions among multiple variables, such as interactive information and total correlation. We finally present an application to feature selection to show how our definition provides a simple yet powerful way to estimate a widely-acknowledged intractable quantity from data. A real example on hyperspectral image (HSI) band selection is also provided.

Request-and-Reverify: Hierarchical Hypothesis Testing for Concept Drift Detection with Expensive Labels

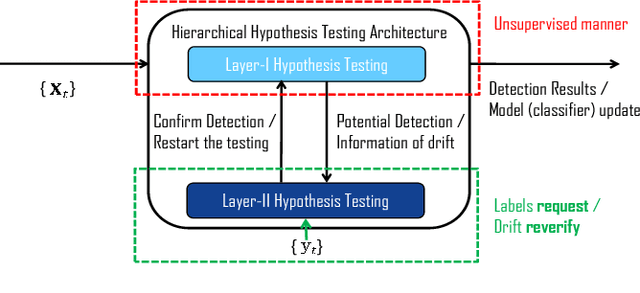
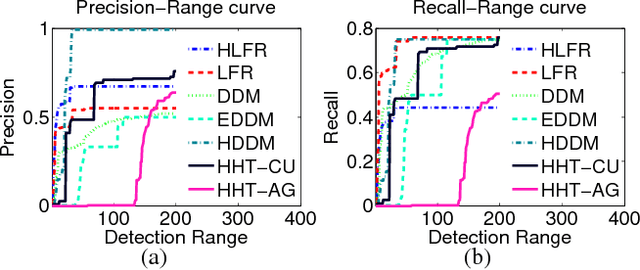
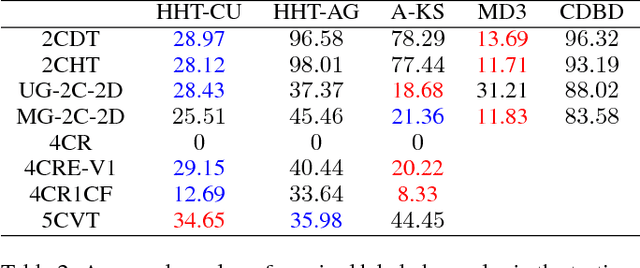
One important assumption underlying common classification models is the stationarity of the data. However, in real-world streaming applications, the data concept indicated by the joint distribution of feature and label is not stationary but drifting over time. Concept drift detection aims to detect such drifts and adapt the model so as to mitigate any deterioration in the model's predictive performance. Unfortunately, most existing concept drift detection methods rely on a strong and over-optimistic condition that the true labels are available immediately for all already classified instances. In this paper, a novel Hierarchical Hypothesis Testing framework with Request-and-Reverify strategy is developed to detect concept drifts by requesting labels only when necessary. Two methods, namely Hierarchical Hypothesis Testing with Classification Uncertainty (HHT-CU) and Hierarchical Hypothesis Testing with Attribute-wise "Goodness-of-fit" (HHT-AG), are proposed respectively under the novel framework. In experiments with benchmark datasets, our methods demonstrate overwhelming advantages over state-of-the-art unsupervised drift detectors. More importantly, our methods even outperform DDM (the widely used supervised drift detector) when we use significantly fewer labels.

An Analysis of the Value of Information when Exploring Stochastic, Discrete Multi-Armed Bandits

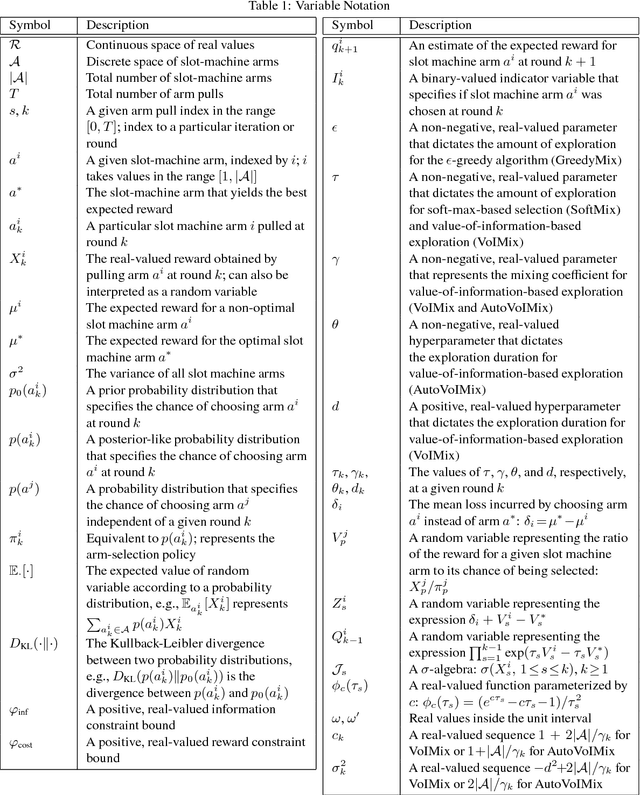
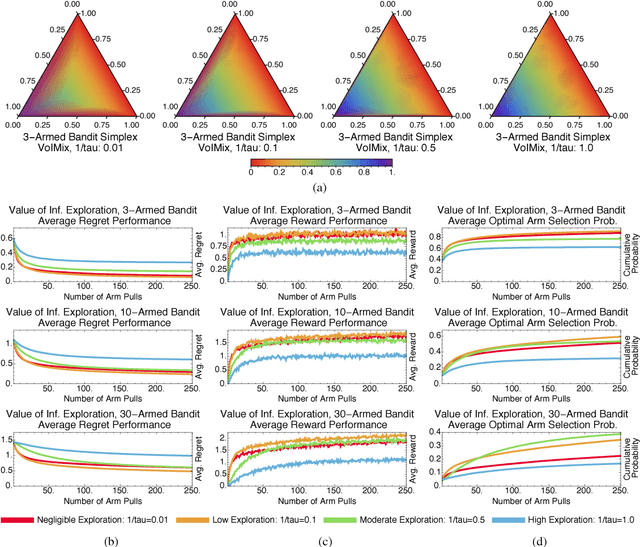
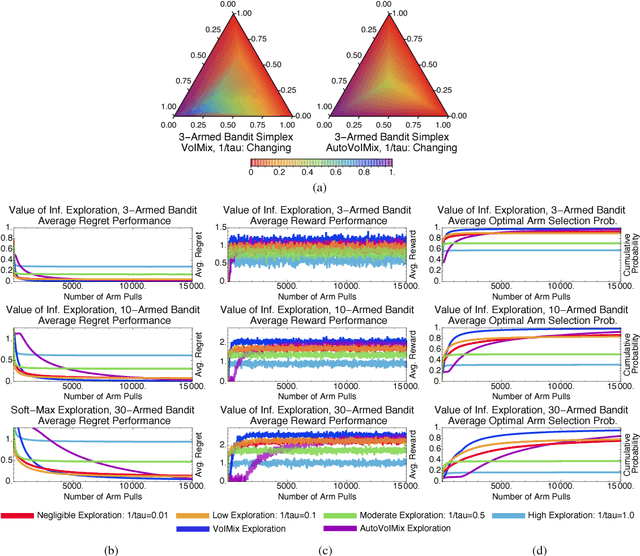
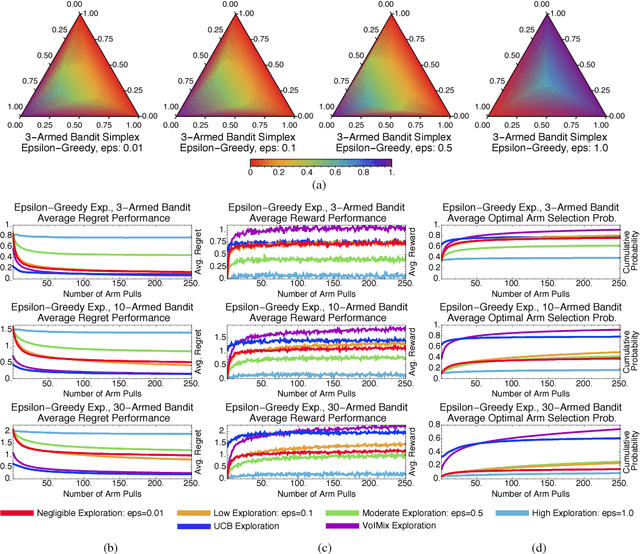
In this paper, we propose an information-theoretic exploration strategy for stochastic, discrete multi-armed bandits that achieves optimal regret. Our strategy is based on the value of information criterion. This criterion measures the trade-off between policy information and obtainable rewards. High amounts of policy information are associated with exploration-dominant searches of the space and yield high rewards. Low amounts of policy information favor the exploitation of existing knowledge. Information, in this criterion, is quantified by a parameter that can be varied during search. We demonstrate that a simulated-annealing-like update of this parameter, with a sufficiently fast cooling schedule, leads to an optimal regret that is logarithmic with respect to the number of episodes.

Guided Policy Exploration for Markov Decision Processes using an Uncertainty-Based Value-of-Information Criterion

Reinforcement learning in environments with many action-state pairs is challenging. At issue is the number of episodes needed to thoroughly search the policy space. Most conventional heuristics address this search problem in a stochastic manner. This can leave large portions of the policy space unvisited during the early training stages. In this paper, we propose an uncertainty-based, information-theoretic approach for performing guided stochastic searches that more effectively cover the policy space. Our approach is based on the value of information, a criterion that provides the optimal trade-off between expected costs and the granularity of the search process. The value of information yields a stochastic routine for choosing actions during learning that can explore the policy space in a coarse to fine manner. We augment this criterion with a state-transition uncertainty factor, which guides the search process into previously unexplored regions of the policy space.

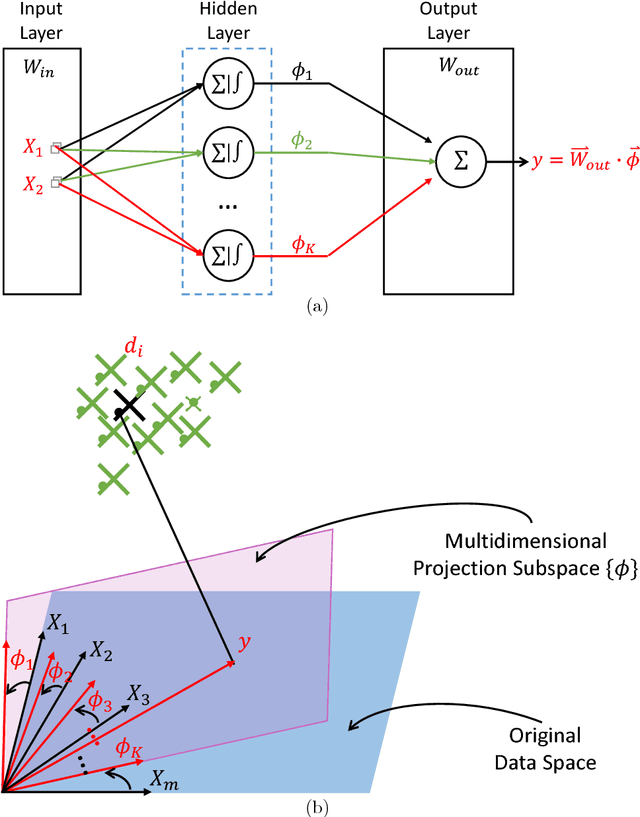
Augmented Space Linear Model

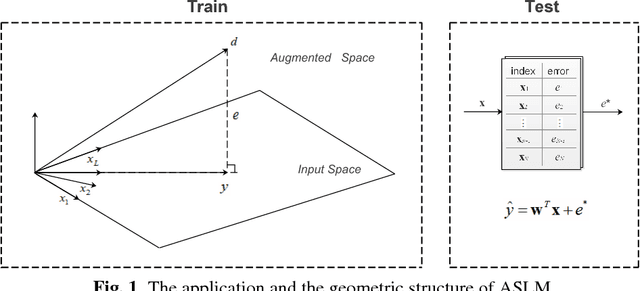
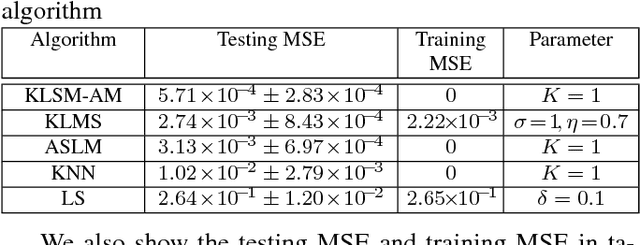
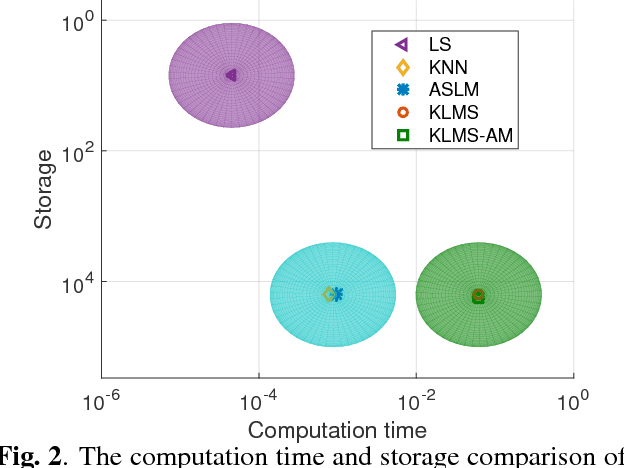
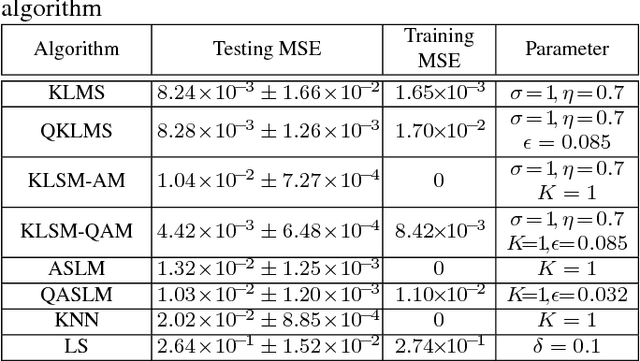
The linear model uses the space defined by the input to project the target or desired signal and find the optimal set of model parameters. When the problem is nonlinear, the adaption requires nonlinear models for good performance, but it becomes slower and more cumbersome. In this paper, we propose a linear model called Augmented Space Linear Model (ASLM), which uses the full joint space of input and desired signal as the projection space and approaches the performance of nonlinear models. This new algorithm takes advantage of the linear solution, and corrects the estimate for the current testing phase input with the error assigned to the input space neighborhood in the training phase. This algorithm can solve the nonlinear problem with the computational efficiency of linear methods, which can be regarded as a trade off between accuracy and computational complexity. Making full use of the training data, the proposed augmented space model may provide a new way to improve many modeling tasks.

Robustness of Maximum Correntropy Estimation Against Large Outliers

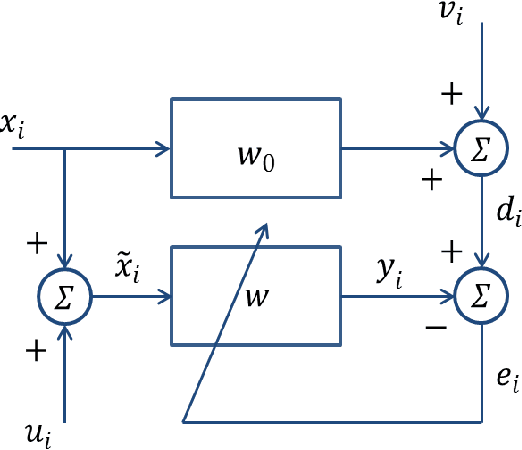
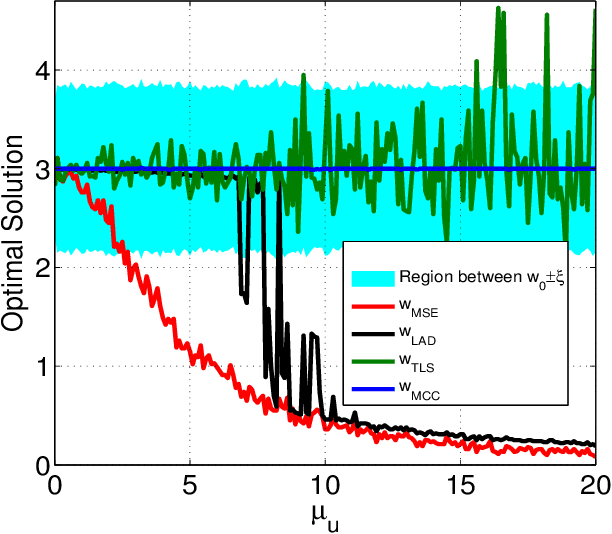
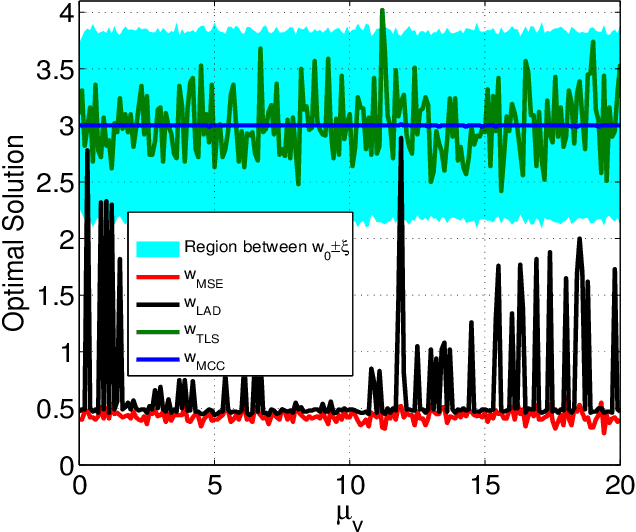
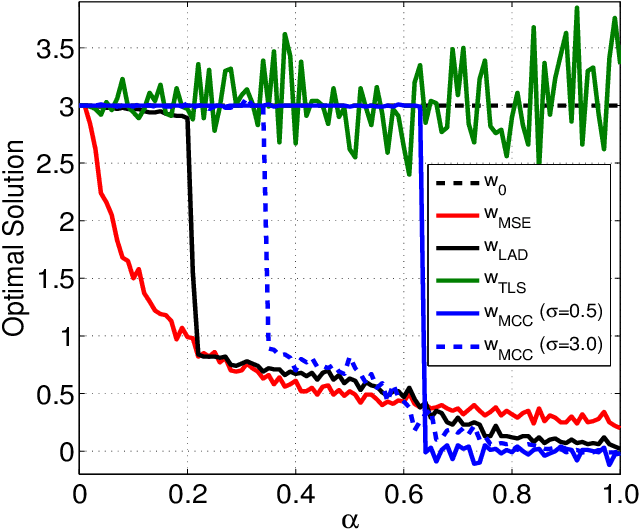
The maximum correntropy criterion (MCC) has recently been successfully applied in robust regression, classification and adaptive filtering, where the correntropy is maximized instead of minimizing the well-known mean square error (MSE) to improve the robustness with respect to outliers (or impulsive noises). Considerable efforts have been devoted to develop various robust adaptive algorithms under MCC, but so far little insight has been gained as to how the optimal solution will be affected by outliers. In this work, we study this problem in the context of parameter estimation for a simple linear errors-in-variables (EIV) model where all variables are scalar. Under certain conditions, we derive an upper bound on the absolute value of the estimation error and show that the optimal solution under MCC can be very close to the true value of the unknown parameter even with outliers (whose values can be arbitrarily large) in both input and output variables. Illustrative examples are presented to verify and clarify the theory.