Towards a Kernel based Physical Interpretation of Model Uncertainty

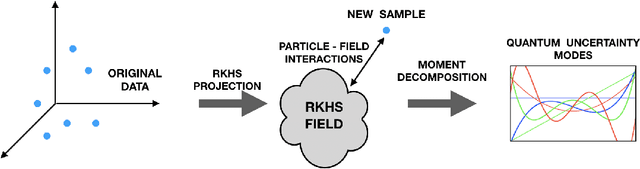
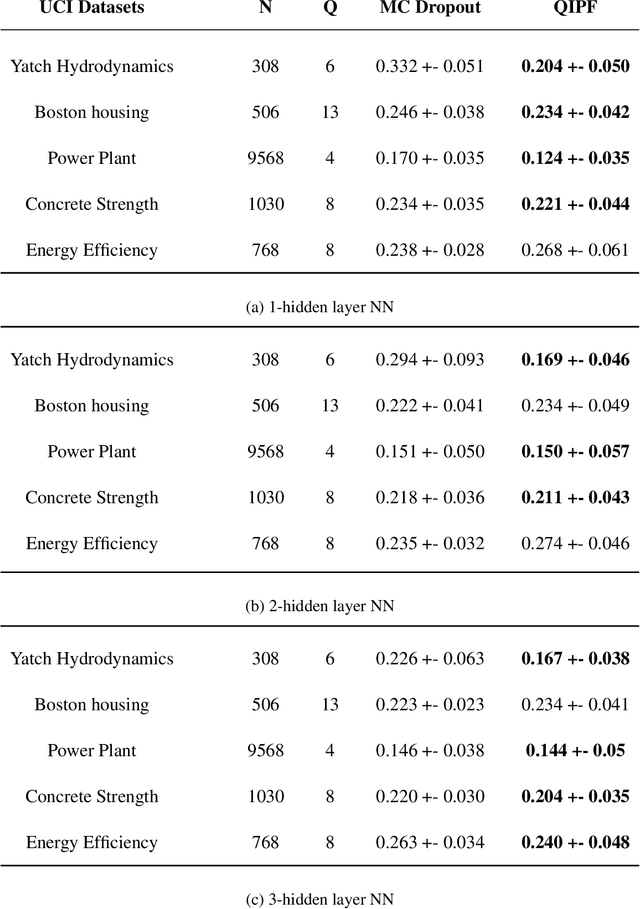
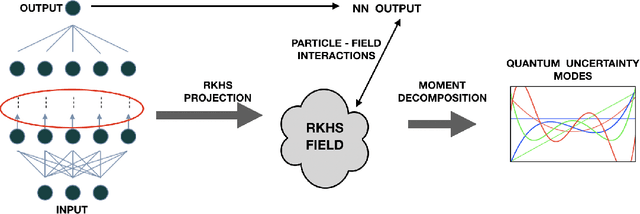
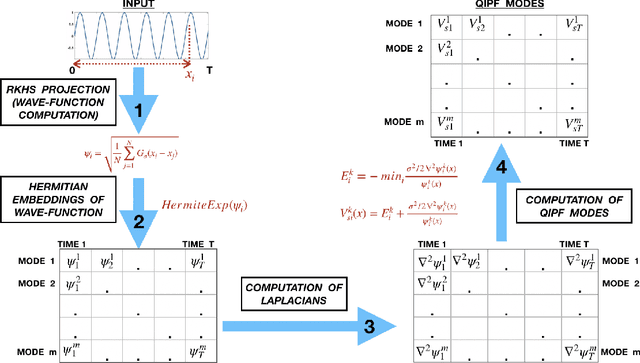
This paper introduces a new information theoretic framework that provides a sensitive multi-modal quantification of data uncertainty by leveraging a quantum physical description of its metric space. We specifically work with the kernel mean embedding metric which yields an intuitive physical interpretation of the signal as a potential field, resulting in its new energy based formulation. This enables one to extract multi-scale uncertainty features of data in the form of information eigenmodes by utilizing moment decomposition concepts of quantum physics. In essence, this approach decomposes local realizations of the signal's PDF in terms of quantum uncertainty moments. We specifically present the application of this framework as a non-parametric and non-intrusive surrogate tool for predictive uncertainty quantification of point-prediction neural network models, overcoming various limitations of conventional Bayesian and ensemble based UQ methods. Experimental comparisons with some established uncertainty quantification methods illustrate performance advantages exhibited by our framework.

Fast Estimation of Information Theoretic Learning Descriptors using Explicit Inner Product Spaces

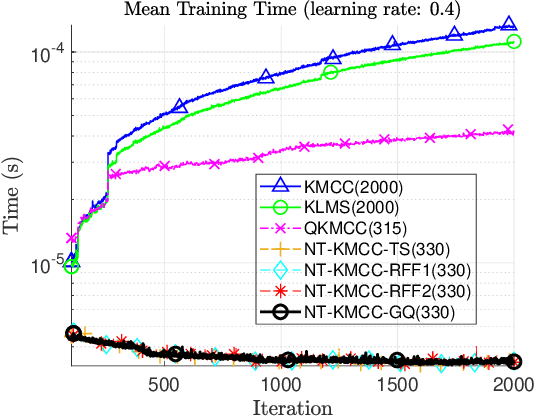
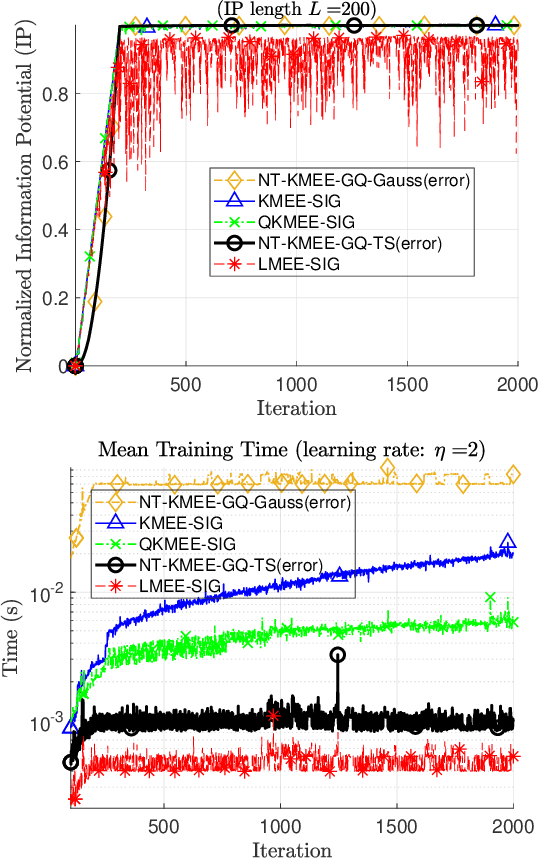
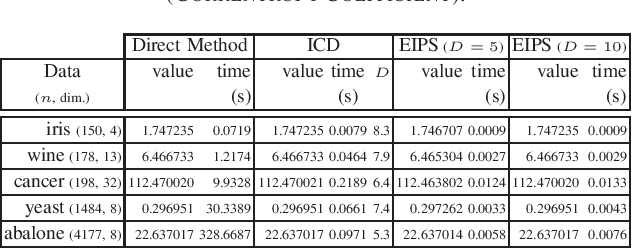
Kernel methods form a theoretically-grounded, powerful and versatile framework to solve nonlinear problems in signal processing and machine learning. The standard approach relies on the \emph{kernel trick} to perform pairwise evaluations of a kernel function, leading to scalability issues for large datasets due to its linear and superlinear growth with respect to the training data. Recently, we proposed \emph{no-trick} (NT) kernel adaptive filtering (KAF) that leverages explicit feature space mappings using data-independent basis with constant complexity. The inner product defined by the feature mapping corresponds to a positive-definite finite-rank kernel that induces a finite-dimensional reproducing kernel Hilbert space (RKHS). Information theoretic learning (ITL) is a framework where information theory descriptors based on non-parametric estimator of Renyi entropy replace conventional second-order statistics for the design of adaptive systems. An RKHS for ITL defined on a space of probability density functions simplifies statistical inference for supervised or unsupervised learning. ITL criteria take into account the higher-order statistical behavior of the systems and signals as desired. However, this comes at a cost of increased computational complexity. In this paper, we extend the NT kernel concept to ITL for improved information extraction from the signal without compromising scalability. Specifically, we focus on a family of fast, scalable, and accurate estimators for ITL using explicit inner product space (EIPS) kernels. We demonstrate the superior performance of EIPS-ITL estimators and combined NT-KAF using EIPS-ITL cost functions through experiments.

No-Trick (Treat) Kernel Adaptive Filtering using Deterministic Features

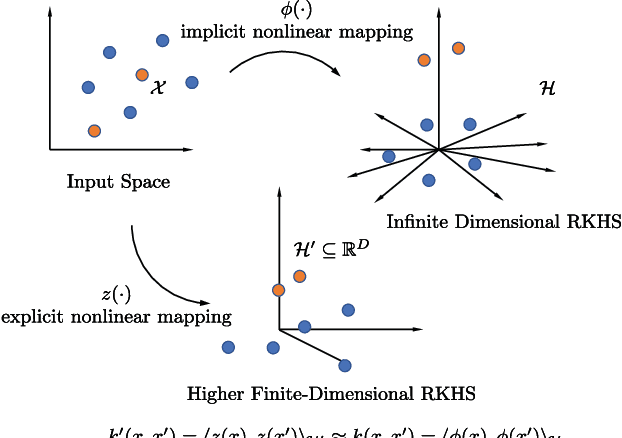
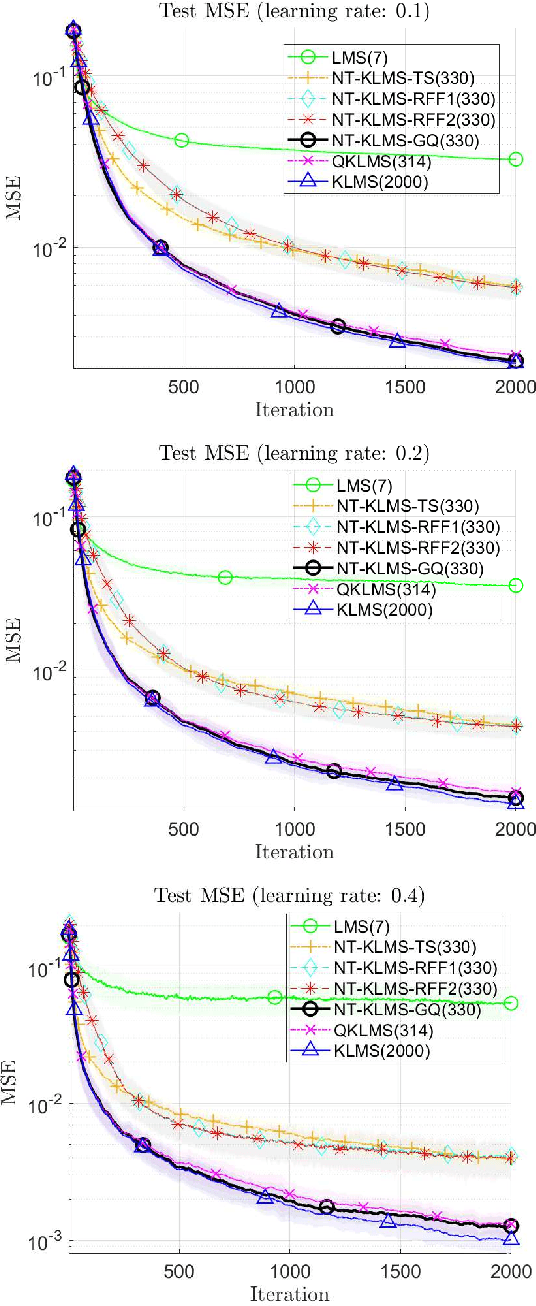
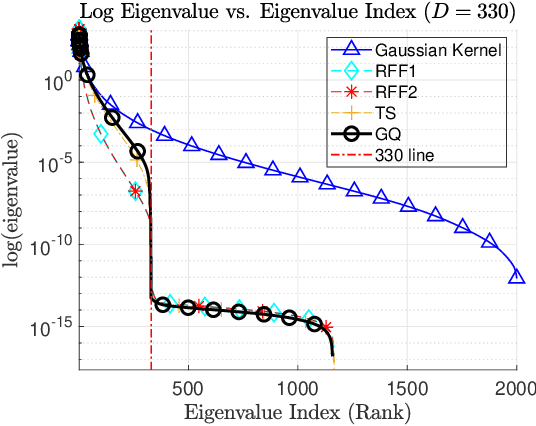
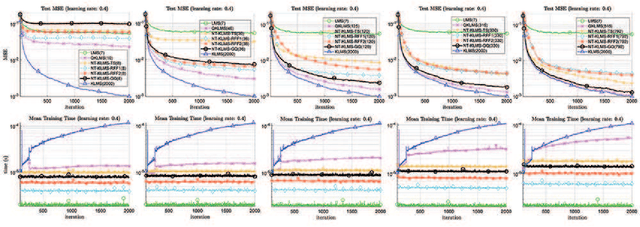
Kernel methods form a powerful, versatile, and theoretically-grounded unifying framework to solve nonlinear problems in signal processing and machine learning. The standard approach relies on the kernel trick to perform pairwise evaluations of a kernel function, which leads to scalability issues for large datasets due to its linear and superlinear growth with respect to the training data. A popular approach to tackle this problem, known as random Fourier features (RFFs), samples from a distribution to obtain the data-independent basis of a higher finite-dimensional feature space, where its dot product approximates the kernel function. Recently, deterministic, rather than random construction has been shown to outperform RFFs, by approximating the kernel in the frequency domain using Gaussian quadrature. In this paper, we view the dot product of these explicit mappings not as an approximation, but as an equivalent positive-definite kernel that induces a new finite-dimensional reproducing kernel Hilbert space (RKHS). This opens the door to no-trick (NT) online kernel adaptive filtering (KAF) that is scalable and robust. Random features are prone to large variances in performance, especially for smaller dimensions. Here, we focus on deterministic feature-map construction based on polynomial-exact solutions and show their superiority over random constructions. Without loss of generality, we apply this approach to classical adaptive filtering algorithms and validate the methodology to show that deterministic features are faster to generate and outperform state-of-the-art kernel methods based on random Fourier features.

Functional Bayesian Filter

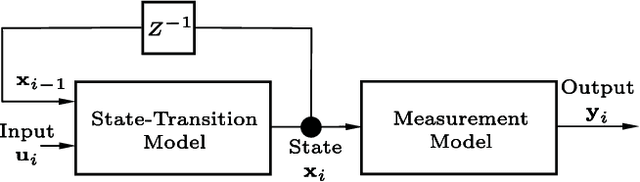
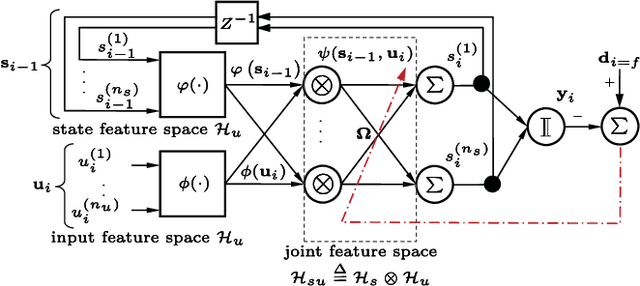
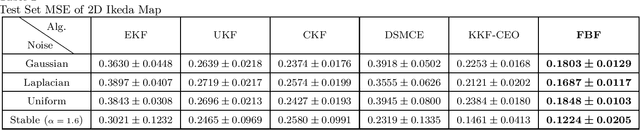
We present a general nonlinear Bayesian filter for high-dimensional state estimation using the theory of reproducing kernel Hilbert space (RKHS). Applying kernel method and the representer theorem to perform linear quadratic estimation in a functional space, we derive a Bayesian recursive state estimator for a general nonlinear dynamical system in the original input space. Unlike existing nonlinear extensions of Kalman filter where the system dynamics are assumed known, the state-space representation for the Functional Bayesian Filter (FBF) is completely learned from measurement data in the form of an infinite impulse response (IIR) filter or recurrent network in the RKHS, with universal approximation property. Using positive definite kernel function satisfying Mercer's conditions to compute and evolve information quantities, the FBF exploits both the statistical and time-domain information about the signal, extracts higher-order moments, and preserves the properties of covariances without the ill effects due to conventional arithmetic operations. This novel kernel adaptive filtering algorithm is applied to recurrent network training, chaotic time-series estimation and cooperative filtering using Gaussian and non-Gaussian noises, and inverse kinematics modeling. Simulation results show FBF outperforms existing Kalman-based algorithms.

Algorithmic Design and Implementation of Unobtrusive Multistatic Serial LiDAR Image

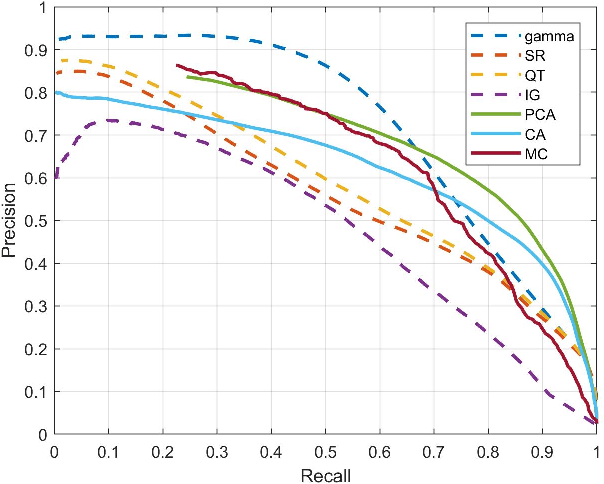
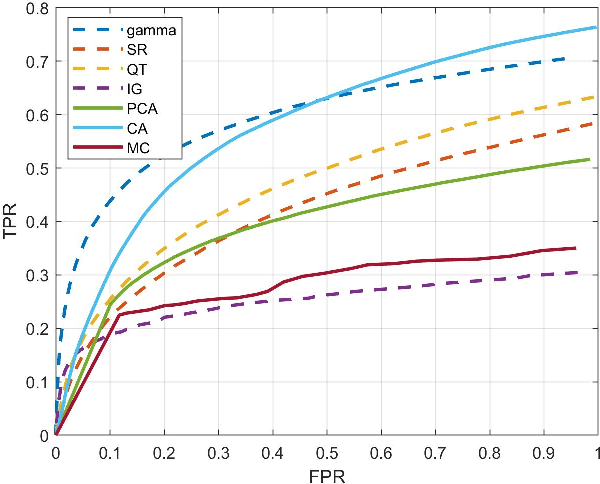
To fully understand interactions between marine hydrokinetic (MHK) equipment and marine animals, a fast and effective monitoring system is required to capture relevant information whenever underwater animals appear. A new automated underwater imaging system composed of LiDAR (Light Detection and Ranging) imaging hardware and a scene understanding software module named Unobtrusive Multistatic Serial LiDAR Imager (UMSLI) to supervise the presence of animals near turbines. UMSLI integrates the front end LiDAR hardware and a series of software modules to achieve image preprocessing, detection, tracking, segmentation and classification in a hierarchical manner.

Multiscale Principle of Relevant Information for Hyperspectral Image Classification

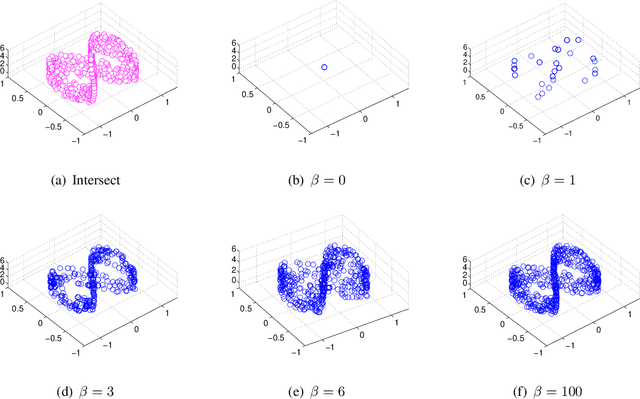
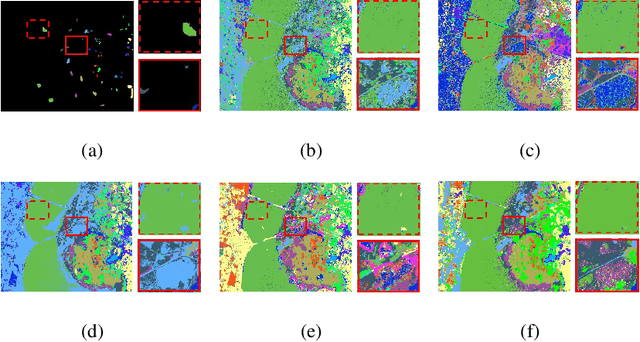
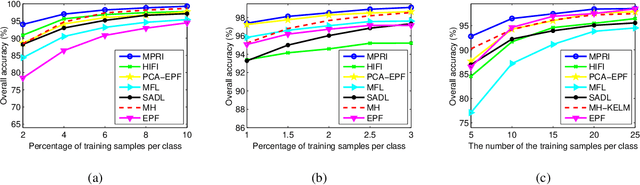
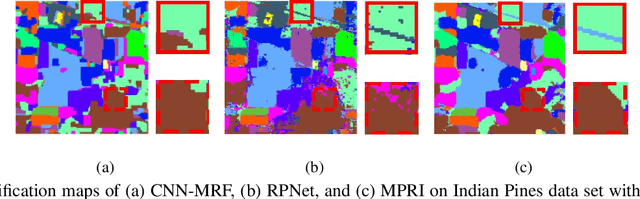
This paper proposes a novel architecture, termed multiscale principle of relevant information (MPRI), to learn discriminative spectral-spatial features for hyperspectral image (HSI) classification. MPRI inherits the merits of the principle of relevant information (PRI) to effectively extract multiscale information embedded in the given data, and also takes advantage of the multilayer structure to learn representations in a coarse-to-fine manner. Specifically, MPRI performs spectral-spatial pixel characterization (using PRI) and feature dimensionality reduction (using regularized linear discriminant analysis) iteratively and successively. Extensive experiments on four benchmark data sets demonstrate that MPRI outperforms existing state-of-the-art HSI classification methods (including deep learning based ones) qualitatively and quantitatively, especially in the scenario of limited training samples.

Maximum Correntropy Criterion with Variable Center

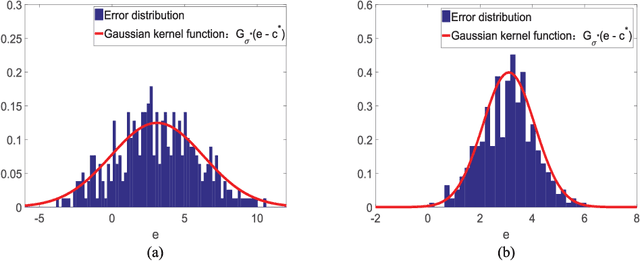
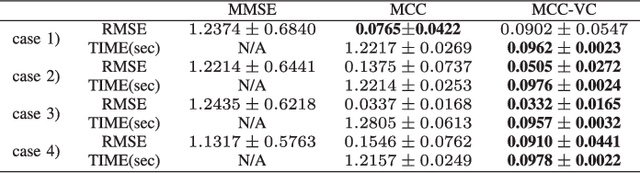
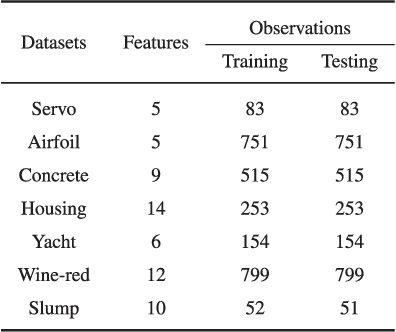
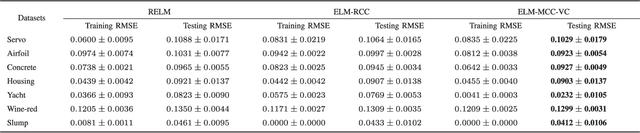
Correntropy is a local similarity measure defined in kernel space and the maximum correntropy criterion (MCC) has been successfully applied in many areas of signal processing and machine learning in recent years. The kernel function in correntropy is usually restricted to the Gaussian function with center located at zero. However, zero-mean Gaussian function may not be a good choice for many practical applications. In this study, we propose an extended version of correntropy, whose center can locate at any position. Accordingly, we propose a new optimization criterion called maximum correntropy criterion with variable center (MCC-VC). We also propose an efficient approach to optimize the kernel width and center location in MCC-VC. Simulation results of regression with linear in parameters (LIP) models confirm the desirable performance of the new method.

An Exact Reformulation of Feature-Vector-based Radial-Basis-Function Networks for Graph-based Observations

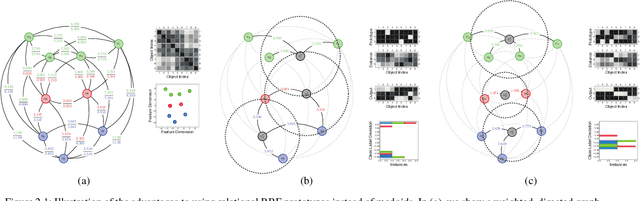
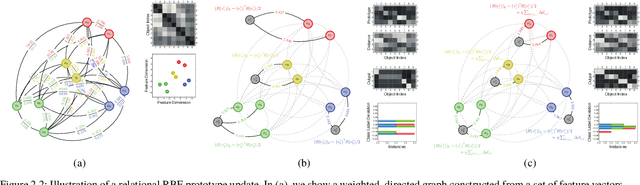
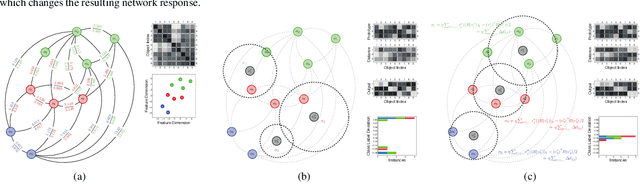
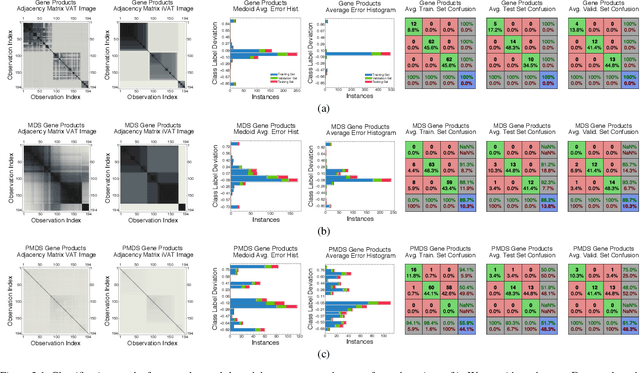
Radial-basis-function networks are traditionally defined for sets of vector-based observations. In this short paper, we reformulate such networks so that they can be applied to adjacency-matrix representations of weighted, directed graphs that represent the relationships between object pairs. We re-state the sum-of-squares objective function so that it is purely dependent on entries from the adjacency matrix. From this objective function, we derive a gradient descent update for the network weights. We also derive a gradient update that simulates the repositioning of the radial basis prototypes and changes in the radial basis prototype parameters. An important property of our radial basis function networks is that they are guaranteed to yield the same responses as conventional radial-basis networks trained on a corresponding vector realization of the relationships encoded by the adjacency-matrix. Such a vector realization only needs to provably exist for this property to hold, which occurs whenever the relationships correspond to distances from some arbitrary metric applied to a latent set of vectors. We therefore completely avoid needing to actually construct vectorial realizations via multi-dimensional scaling, which ensures that the underlying relationships are totally preserved.

Theory and Algorithms for Pulse Signal Processing

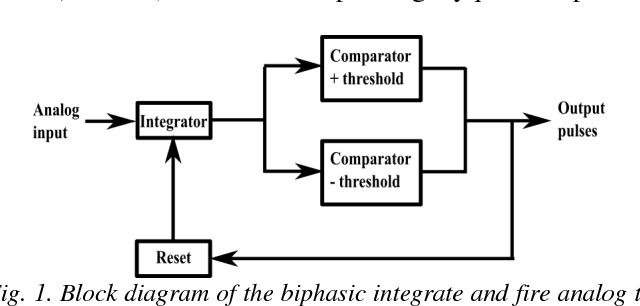
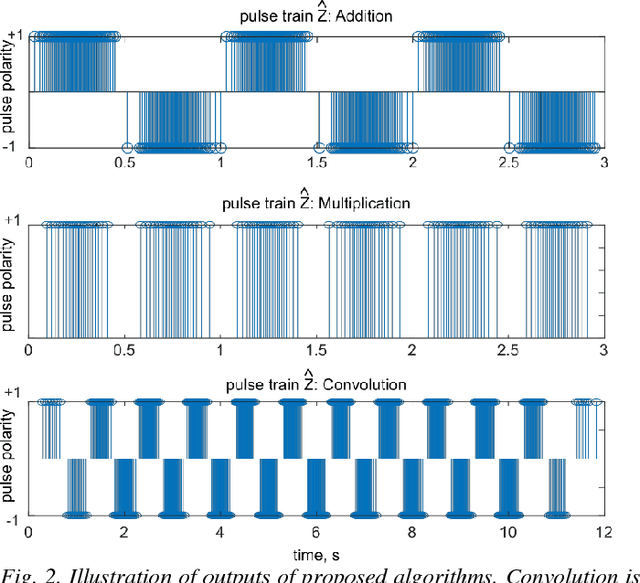
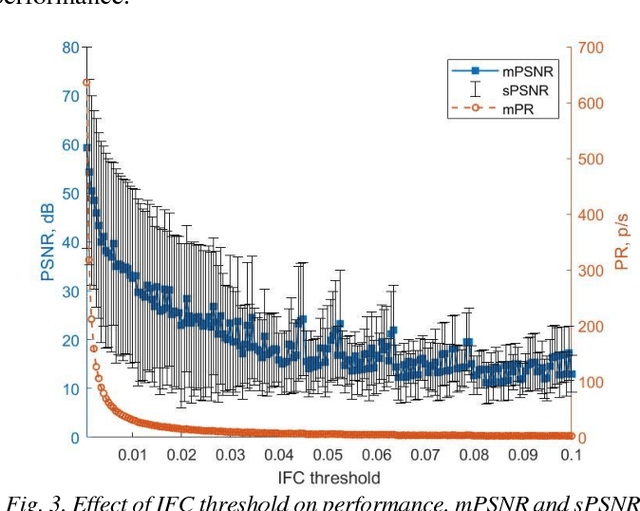
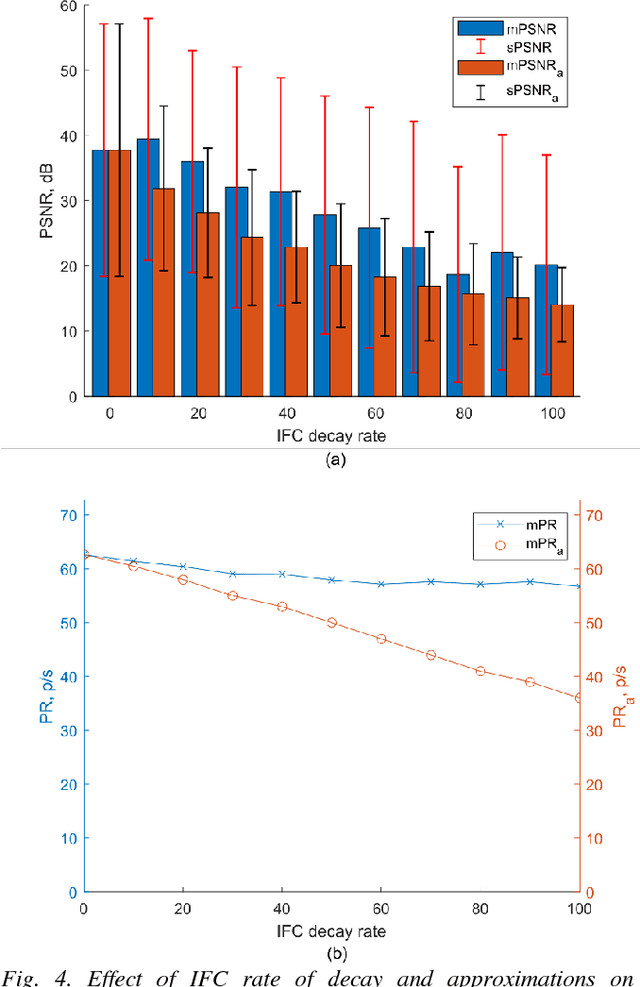
The integrate and fire converter transforms an analog signal into train of biphasic pulses. The pulse train has information encoded in the timing and polarity of pulses. While it has been shown that any finite bandwidth analog signal can be reconstructed from these pulse trains with an error as small as desired, there is a need for fundamental signal processing techniques to operate directly on pulse trains without signal reconstruction. In this paper, the feasibility of performing online the signal processing operations of addition, multiplication, and convolution of analog signals using their pulses train representations is explored. Theoretical framework to perform signal processing with pulse trains imposing minimal restrictions is derived, and algorithms for online implementation of the operators are developed. Performance of the algorithms in processing simulated data is studied. An application of noise subtraction and representation of relevant features of interest in electrocardiogram signal is demonstrated with mean pulse rate less than 20 pulses per second.

Simple stopping criteria for information theoretic feature selection

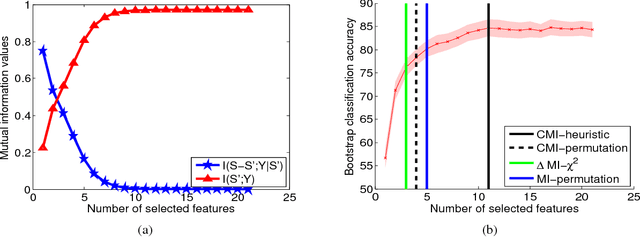
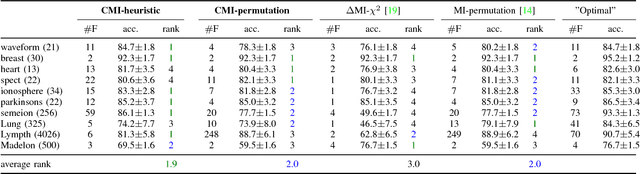
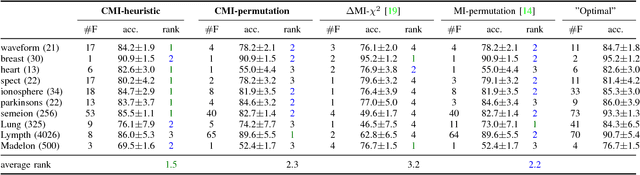
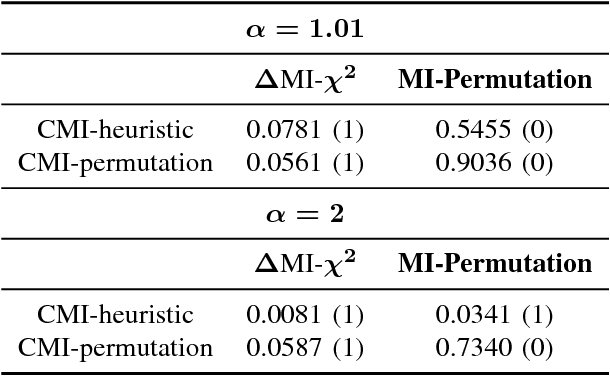
Information theoretic feature selection aims to select a smallest feature subset such that the mutual information between the selected features and the class labels is maximized. Despite the simplicity of this objective, there still remains several open problems to optimize it. These include, for example, the automatic determination of the optimal subset size (i.e., the number of features) or a stopping criterion if the greedy searching strategy is adopted. In this letter, we suggest two stopping criteria by just monitoring the conditional mutual information (CMI) among groups of variables. Using the recently developed multivariate matrix-based Renyi's \alpha-entropy functional, we show that the CMI among groups of variables can be easily estimated without any decomposition or approximation, hence making our criteria easily implemented and seamlessly integrated into any existing information theoretic feature selection methods with greedy search strategy.