Towards a Kernel based Physical Interpretation of Model Uncertainty

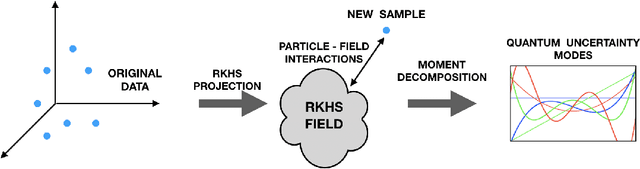
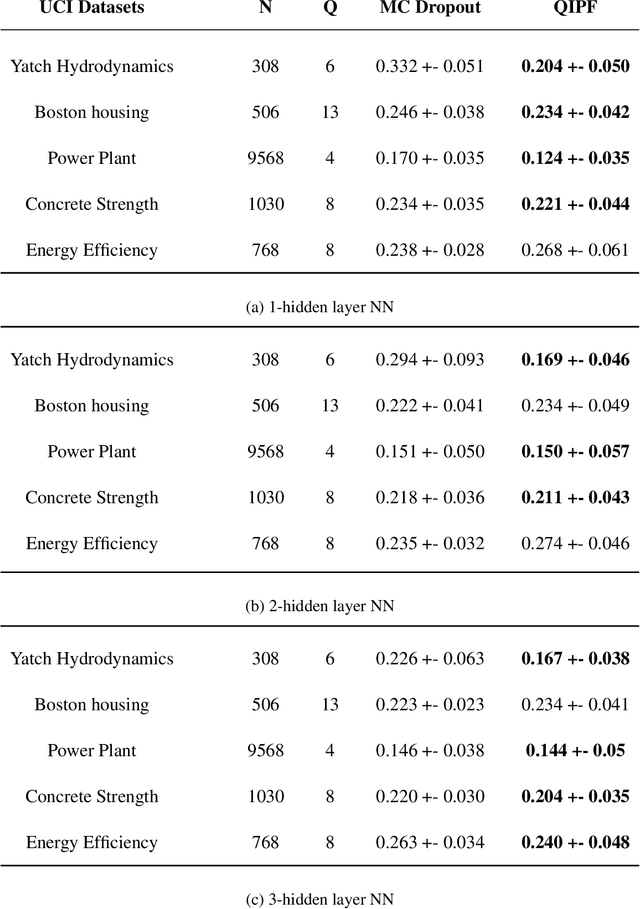
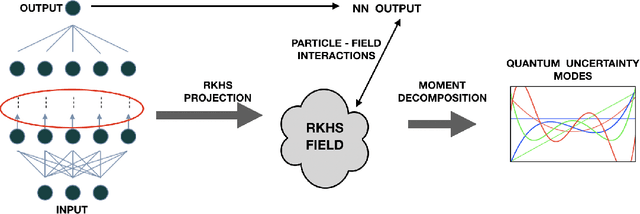
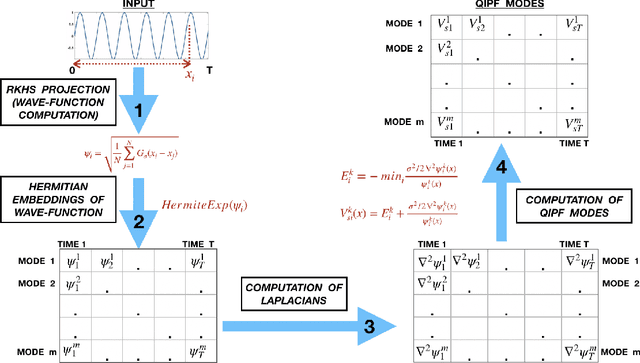
This paper introduces a new information theoretic framework that provides a sensitive multi-modal quantification of data uncertainty by leveraging a quantum physical description of its metric space. We specifically work with the kernel mean embedding metric which yields an intuitive physical interpretation of the signal as a potential field, resulting in its new energy based formulation. This enables one to extract multi-scale uncertainty features of data in the form of information eigenmodes by utilizing moment decomposition concepts of quantum physics. In essence, this approach decomposes local realizations of the signal's PDF in terms of quantum uncertainty moments. We specifically present the application of this framework as a non-parametric and non-intrusive surrogate tool for predictive uncertainty quantification of point-prediction neural network models, overcoming various limitations of conventional Bayesian and ensemble based UQ methods. Experimental comparisons with some established uncertainty quantification methods illustrate performance advantages exhibited by our framework.