Jong-Shi Pang
Offline Policy Learning with Weight Clipping and Heaviside Composite Optimization
Jan 17, 2026Abstract:Offline policy learning aims to use historical data to learn an optimal personalized decision rule. In the standard estimate-then-optimize framework, reweighting-based methods (e.g., inverse propensity weighting or doubly robust estimators) are widely used to produce unbiased estimates of policy values. However, when the propensity scores of some treatments are small, these reweighting-based methods suffer from high variance in policy value estimation, which may mislead the downstream policy optimization and yield a learned policy with inferior value. In this paper, we systematically develop an offline policy learning algorithm based on a weight-clipping estimator that truncates small propensity scores via a clipping threshold chosen to minimize the mean squared error (MSE) in policy value estimation. Focusing on linear policies, we address the bilevel and discontinuous objective induced by weight-clipping-based policy optimization by reformulating the problem as a Heaviside composite optimization problem, which provides a rigorous computational framework. The reformulated policy optimization problem is then solved efficiently using the progressive integer programming method, making practical policy learning tractable. We establish an upper bound for the suboptimality of the proposed algorithm, which reveals how the reduction in MSE of policy value estimation, enabled by our proposed weight-clipping estimator, leads to improved policy learning performance.
Statistical Analysis of Stationary Solutions of Coupled Nonconvex Nonsmooth Empirical Risk Minimization
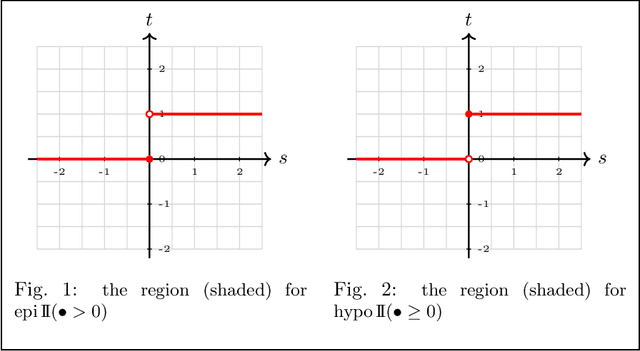
Oct 06, 2019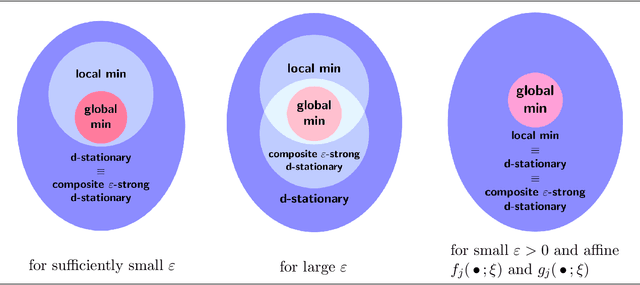
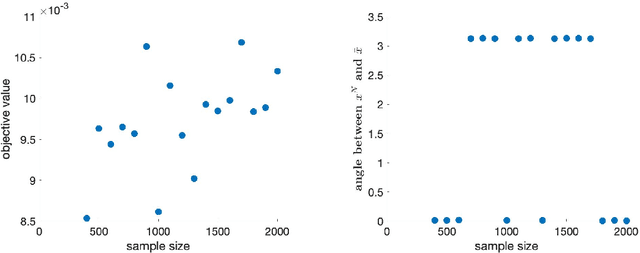
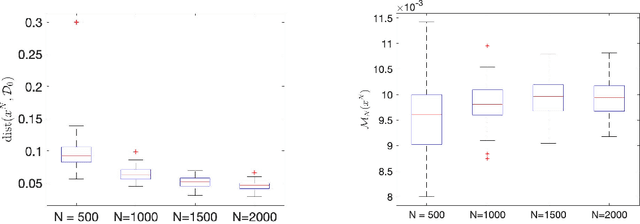
Abstract:This paper has two main goals: (a) establish several statistical properties---consistency, asymptotic distributions, and convergence rates---of stationary solutions and values of a class of coupled nonconvex and nonsmoothempirical risk minimization problems, and (b) validate these properties by a noisy amplitude-based phase retrieval problem, the latter being of much topical interest.Derived from available data via sampling, these empirical risk minimization problems are the computational workhorse of a population risk model which involves the minimization of an expected value of a random functional. When these minimization problems are nonconvex, the computation of their globally optimal solutions is elusive. Together with the fact that the expectation operator cannot be evaluated for general probability distributions, it becomes necessary to justify whether the stationary solutions of the empirical problems are practical approximations of the stationary solution of the population problem. When these two features, general distribution and nonconvexity, are coupled with nondifferentiability that often renders the problems "non-Clarke regular", the task of the justification becomes challenging. Our work aims to address such a challenge within an algorithm-free setting. The resulting analysis is therefore different from the much of the analysis in the recent literature that is based on local search algorithms. Furthermore, supplementing the classical minimizer-centric analysis, our results offer a first step to close the gap between computational optimization and asymptotic analysis of coupled nonconvex nonsmooth statistical estimation problems, expanding the former with statistical properties of the practically obtained solution and providing the latter with a more practical focus pertaining to computational tractability.
Estimation of Individualized Decision Rules Based on an Optimized Covariate-Dependent Equivalent of Random Outcomes
Aug 27, 2019
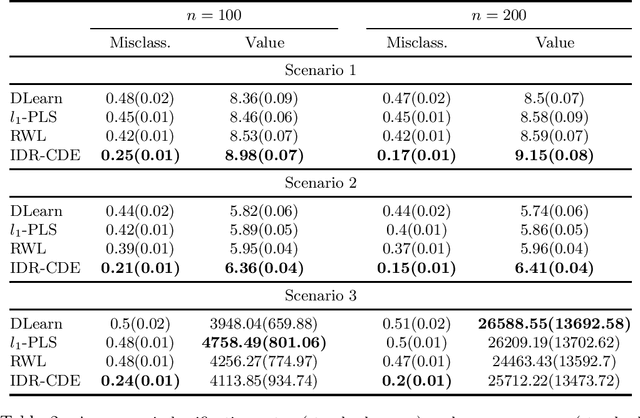
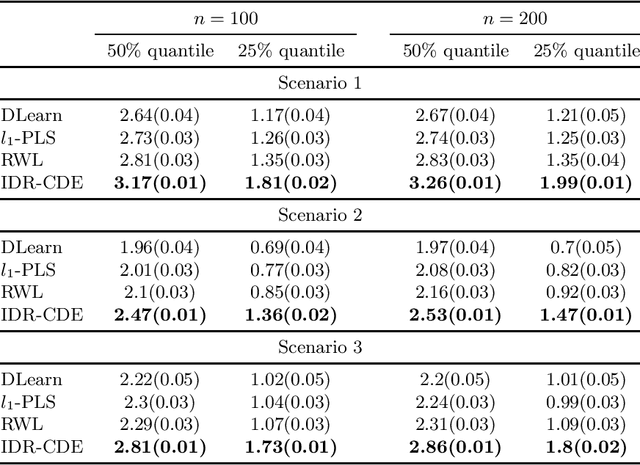
Abstract:Recent exploration of optimal individualized decision rules (IDRs) for patients in precision medicine has attracted a lot of attention due to the heterogeneous responses of patients to different treatments. In the existing literature of precision medicine, an optimal IDR is defined as a decision function mapping from the patients' covariate space into the treatment space that maximizes the expected outcome of each individual. Motivated by the concept of Optimized Certainty Equivalent (OCE) introduced originally in \cite{ben1986expected} that includes the popular conditional-value-of risk (CVaR) \cite{rockafellar2000optimization}, we propose a decision-rule based optimized covariates dependent equivalent (CDE) for individualized decision making problems. Our proposed IDR-CDE broadens the existing expected-mean outcome framework in precision medicine and enriches the previous concept of the OCE. Numerical experiments demonstrate that our overall approach outperforms existing methods in estimating optimal IDRs under heavy-tail distributions of the data.
Clustering by Orthogonal NMF Model and Non-Convex Penalty Optimization
Jun 03, 2019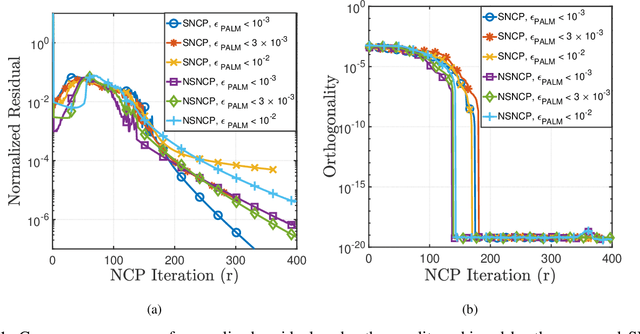
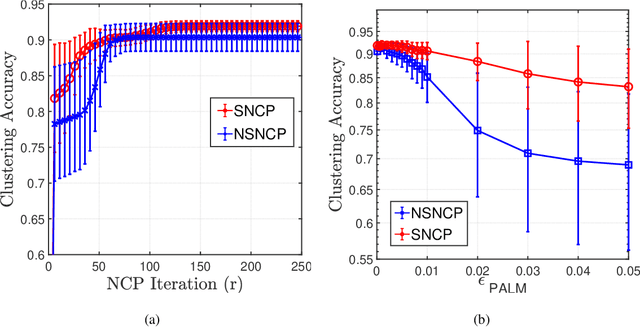
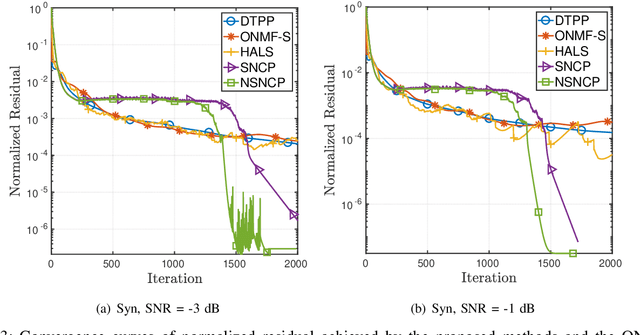
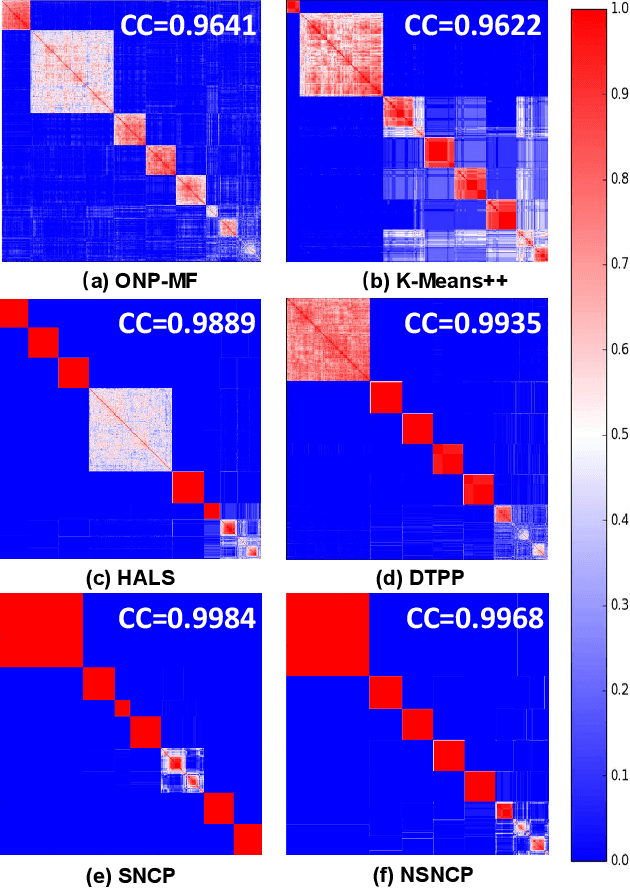
Abstract:The non-negative matrix factorization (NMF) model with an additional orthogonality constraint on one of the factor matrices, called the orthogonal NMF (ONMF), has been found to provide improved clustering performance over the K-means. Solving the ONMF model is a challenging optimization problem due to the existence of both orthogonality and nonnegativity constraints, and most of the existing methods directly deal with the orthogonality constraint in its original form via various optimization techniques. In this paper, we propose a new ONMF based clustering formulation that equivalently transforms the orthogonality constraint into a set of norm-based non-convex equality constraints. We then apply a non-convex penalty (NCP) approach to add the non-convex equality constraints to the objective as penalty terms, leaving simple non-negativity constraints only in the penalized problem. One smooth penalty formulation and one non-smooth penalty formulation are respectively studied, and theoretical conditions for the penalized problems to provide feasible stationary solutions to the ONMF based clustering problem are presented. Experimental results based on both synthetic and real datasets are presented to show that the proposed NCP methods are computationally time efficient, and either match or outperform the existing K-means and ONMF based methods in terms of the clustering performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge